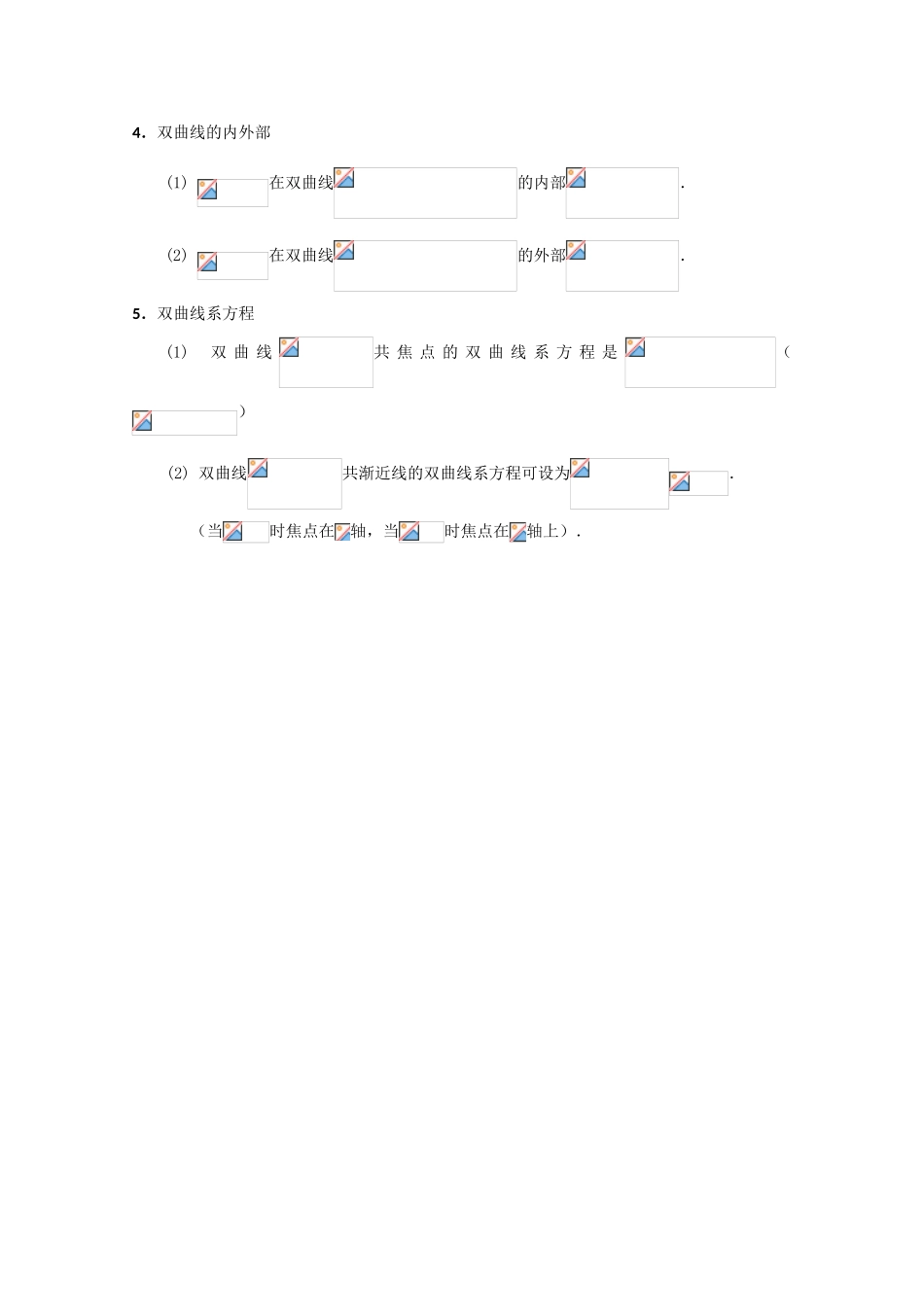
数学选修 1-1 知识点第 2 章 圆锥曲线与方程 (2)双曲线1.双曲线定义:在平面内,到两个定点 F1、F2的距离的差的绝对值等于常数(小于|F1F2|) (为常数)的点的轨迹叫做双曲线.⑴ 若 2<,则动点 P 的轨迹是双曲线.⑵ 若 2=,则动点 P 的轨迹是以 F1,F2为端点的两条射线(在直线 F1,F2上).⑶ 若 2>,则动点 P 无轨迹.2.双曲线的标准方程:焦点在轴上时,方程为 焦点焦点在轴上时,方程为 焦点注:(类比勾股定理)双曲线的一般方程:注:方程(均不为 0)表示双曲线的条件:方程变形:,考察二次项系数的正负,若与异号,表示双曲线;若同号且,则表示椭圆;若同号且=,则表示圆.3.双曲线的性质:(1)范围:或,.(2)对称性:关于轴、轴、原点对称.(3)顶点坐标:双曲线和轴有两个交点,焦点坐标是.(4)实轴长 2、虚轴长 2、焦距 2;实半轴、虚半轴、半焦距.(5)双曲线的准线方程是,准线到中心的距离为,焦准距:(焦点到对应准线的距离).通径的长是,通径的一半(半通径):.(6) 渐近线方程是① 双曲线渐近线方程:令,即;② 渐近线是 (或)的双曲线设为.(λ≠0),k 是待定系数.③(焦渐距)焦点到渐近线的距离恒为.(7) 等轴双曲线:实轴和虚轴等长的双曲线叫做等轴双曲线. 定义式:.注:①等轴双曲线的渐近线方程为: .②渐近线互相垂直. ③ 等轴双曲线可设为:.(时焦点在轴,时焦点在轴上)(8) 离心率是 ()越大,开口越开阔;越小,开口越扁狭.(9) 半径:若点是双曲线上一点,是其左、右焦点, , 即焦半径:点在左支上 和.点在右支上 和.4.双曲线的内外部(1) 在双曲线的内部.(2) 在双曲线的外部.5.双曲线系方程(1) 双 曲 线共 焦 点 的 双 曲 线 系 方 程 是()(2) 双曲线共渐近线的双曲线系方程可设为.(当时焦点在轴,当时焦点在轴上).