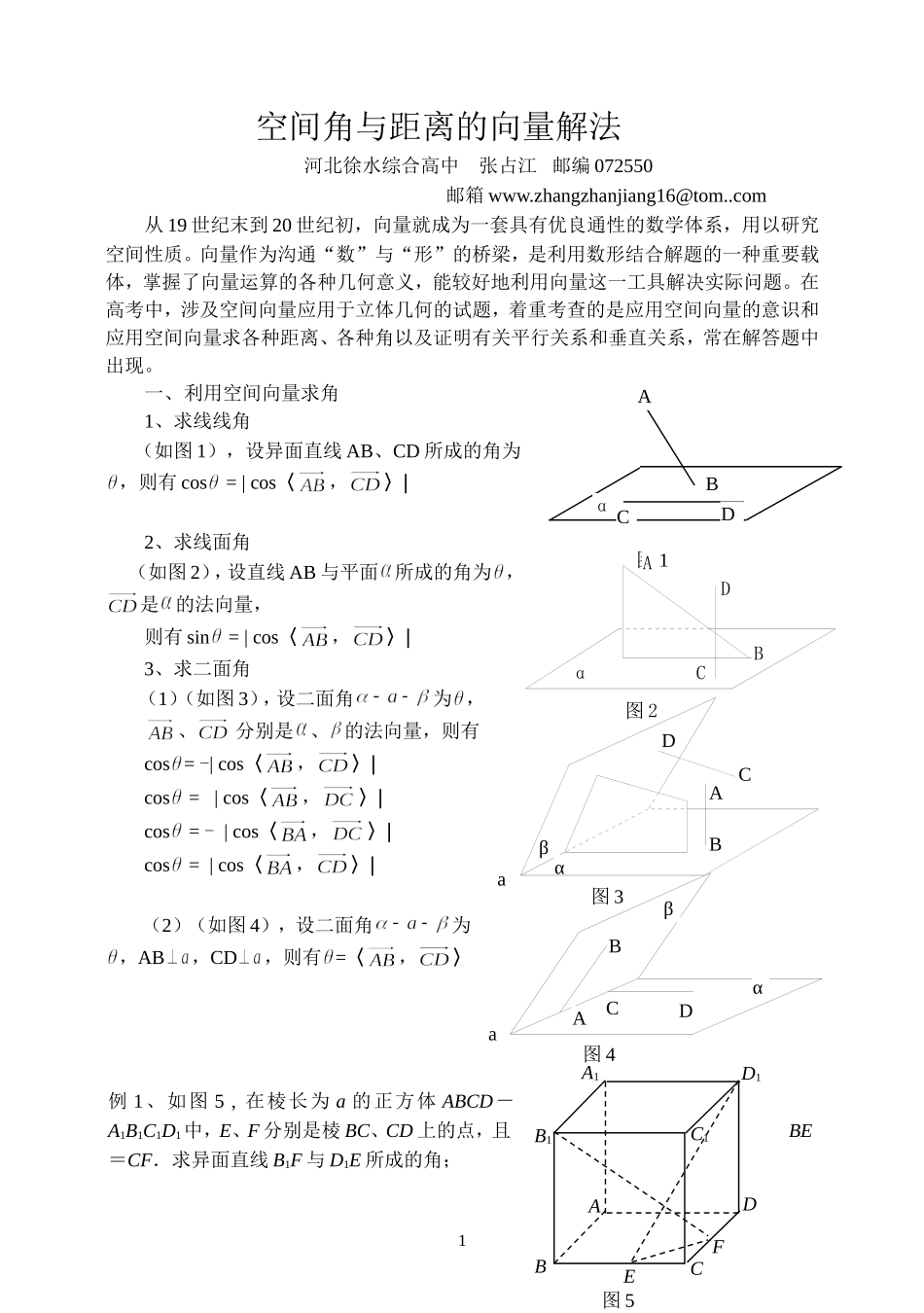
空间角与距离的向量解法河北徐水综合高中 张占江 邮编 072550邮箱 www.zhangzhanjiang16@tom..com从 19 世纪末到 20 世纪初,向量就成为一套具有优良通性的数学体系,用以研究空间性质。向量作为沟通“数”与“形”的桥梁,是利用数形结合解题的一种重要载体,掌握了向量运算的各种几何意义,能较好地利用向量这一工具解决实际问题。在高考中,涉及空间向量应用于立体几何的试题,着重考查的是应用空间向量的意识和应用空间向量求各种距离、各种角以及证明有关平行关系和垂直关系,常在解答题中出现。一、利用空间向量求角1、求线线角(如图 1),设异面直线 AB、CD 所成的角为,则有 cos = | cos〈,〉|2、求线面角(如图 2),设直线 AB 与平面所成的角为 ,是的法向量,则有 sin = | cos〈,〉|3、求二面角(1)(如图 3),设二面角为 ,、 分别是、 的法向量,则有cos = -| cos〈,〉|cos = | cos〈,〉|cos = - | cos〈,〉|cos = | cos〈,〉|(2)(如图 4),设二面角为,AB,CD,则有 =〈,〉例 1、如图 5 , 在棱长为 a 的正方体 ABCD-A1B1C1D1中,E、F 分别是棱 BC、CD 上的点,且BE=CF.求异面直线 B1F 与 D1E 所成的角; 1ABCDα图 1αABCD图 2βαDCBAa图 3DAB图 4aCαβABCDD1A1B1C1EF图 5解:以 A 为原点,分别以为 x 轴、y轴、z 轴建立空间直角坐标系,如图 6 设 BE=x,则有 B1(a,0,a),D1(0,a,a),E(a,x,0),F(a-x,a,0) ∴ ∴ 因此,B1F⊥D1E.即 B1F 与 D1E 所成的角为 90 说明:本题也可利用线面垂直来证明 B1F⊥D1E,也可通过平移直接求异面直线 B1F 与 D1E 所成的角,如图 7,连接BF、AE、A1D、AD1,在正方形 ABCD 中,由 BE=CF 可证得 BF AE,又 BF 为 B1F 在底面 ABCD 上的射影,B1FAE,又 B1F 在面 A1ADD1上的射影为 A1D,而 A1DAD1, B1F AD1,又 AD1 AE=A,B1F 面 AED1,而D1E面 AED1 B1F⊥D1E。 显然,利用此法比利用向量解要复杂的多,本题充分体现了利用向量法解决立体几何问题的优越性。例 2、如图 8,四棱锥 P - ABCD 中,PD 底面ABCD,底面 ABCD是直角梯形,BAD = ADC = 90 ,AB = AD = PD = 2,CD = 4,E 是 PB 的中点,以DA、DC、DP 分别为 x 轴、y 轴、z 轴建立直角坐标系。(1)若 点 F平 面 ABCD , 且 FE 面PBC,,求 F 点坐标;(...