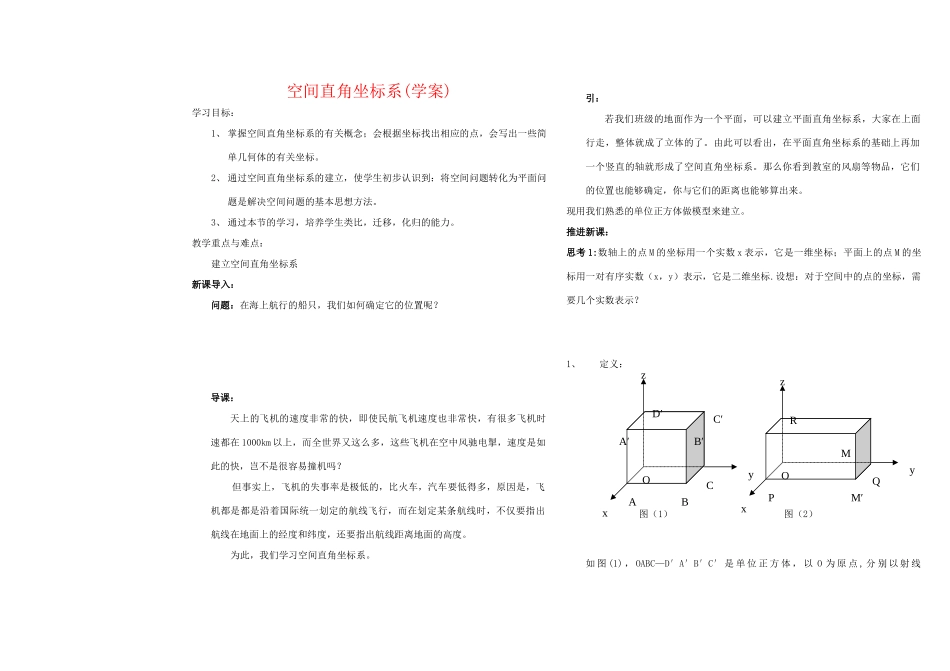
空间直角坐标系(学案)学习目标:1、 掌握空间直角坐标系的有关概念;会根据坐标找出相应的点,会写出一些简单几何体的有关坐标。2、 通过空间直角坐标系的建立,使学生初步认识到:将空间问题转化为平面问题是解决空间问题的基本思想方法。3、 通过本节的学习,培养学生类比,迁移,化归的能力。教学重点与难点:建立空间直角坐标系新课导入:问题:在海上航行的船只,我们如何确定它的位置呢?导课:天上的飞机的速度非常的快,即使民航飞机速度也非常快,有很多飞机时速都在 1000km 以上,而全世界又这么多,这些飞机在空中风驰电掣,速度是如此的快,岂不是很容易撞机吗? 但事实上,飞机的失事率是极低的,比火车,汽车要低得多,原因是,飞机都是都是沿着国际统一划定的航线飞行,而在划定某条航线时,不仅要指出航线在地面上的经度和纬度,还要指出航线距离地面的高度。 为此,我们学习空间直角坐标系。引:若我们班级的地面作为一个平面,可以建立平面直角坐标系,大家在上面行走,整体就成了立体的了。由此可以看出,在平面直角坐标系的基础上再加一个竖直的轴就形成了空间直角坐标系。那么你看到教室的风扇等物品,它们的位置也能够确定,你与它们的距离也能够算出来。现用我们熟悉的单位正方体做模型来建立。推进新课:思考 1:数轴上的点 M 的坐标用一个实数 x 表示,它是一维坐标;平面上的点 M 的坐标用一对有序实数(x,y)表示,它是二维坐标.设想:对于空间中的点的坐标,需要几个实数表示?1、定义:图(1) 图(2)如 图 (1) , OABC—D′A′B′C′ 是 单 位 正 方 体 , 以 O 为 原 点 , 分 别 以 射 线ABCzxyOA′B′C′D′zxyORPQMM′OA,OC,OD′的方向为正方向,以线段 OA,OC,OD′的长为单位长,建立三条数轴:x 轴、y 轴、z 轴。这时我们说建立了一个__________________Oxyz。其中点 O 叫做__________,x 轴、y 轴、z 轴叫做________。通过每两个坐标轴的平面叫做_________,分别称为 xOy 平面、yOz 平面、zOx 平面。右手直角坐标系:在空间直角坐标系中,让右手_____ 指向 x 轴正方向,_____指向 y 轴正方向,如果_______指向 z 轴正方向,则称这个坐标系为右手直角坐标系。注:如无特殊说明,课本建立的坐标系,都是右手直角坐标系。如图(2),设点 M 为空间的一个定点,过点 M 分别作垂直于 x 轴、y 轴和 z 轴的平面,依次交 x 轴、y 轴和 z ...