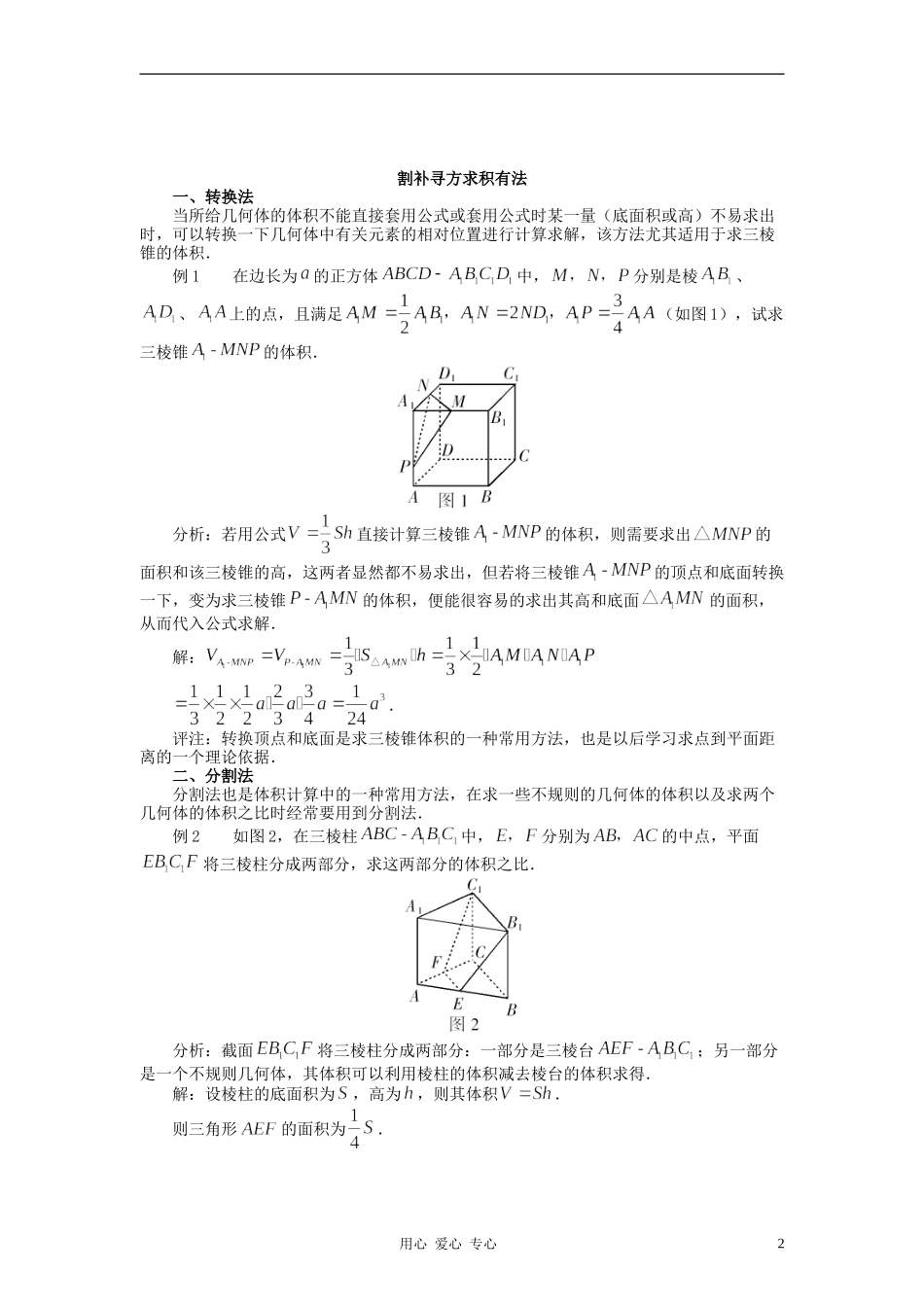
1.8m1.2m5m几何体表面积与体积的应用在我们的生活中各种各样的物体,都是由一些简单的几何体组合而成。几何体表面积的大小以及所占空间体积的大小,都与我们的生活息息相关。本文准备从以下几个方面来研究空间几何体的表面积和体积。 1.侧面积(表面积)的计算 例 1.牧民居住的蒙古包的形状是一个圆柱与圆锥的组合体, 尺寸如图所示。请你计算要搭建这样的一个蒙古包至少需要多少平方米的篷布?(精确到 0.01m2) 解:上部分圆锥的母线长为,其侧面积为, 下部分圆柱的侧面积, 所以,要搭建这样的一个蒙古包至少需要的篷布为: 答:要搭建这样的一个蒙古包至少需要 50.05 平方米的篷布。点评:解实际问题时,要注意区分求的是面积还是体积,是表面积还是侧面积。2.体积相关计算例 2.现有一个长方体水箱,从水箱里面量得它的深是 30cm,底面的长是 25cm,宽是20cm。设水箱里盛有深为 acm 的水。若往水箱里放入棱长为 10cm 的正方形铁块,试求现在的水深?解:设放入正方体铁块后水深为 hcm。 当放入正方体铁块后,若水面刚好与正方体上面相平时,由 25 20 10=25 20a+1010 10,解得 a=8; 当放入正方体铁块后,若水面刚好与正方体水箱相平时,由 25 20 30=25 20a+1010 10,解得 a=28。 所以,当时,放入正方体铁块后没有被水淹没,则 25 20h=25 20a+1010h,解得 h=; 当时,放入正方体铁块后被水淹没,则 25 20h=25 20a+10 10 10,解得h=a+2; 当时,放入正方体铁块后水箱里的水将溢出,这时 h=30。 综上所得, 。点评:本题是通过体积关系建立方程而求解的。在解题的过程中一定要注意根据实际情形进行分类讨论。用心 爱心 专心1割补寻方求积有法一、转换法 当所给几何体的体积不能直接套用公式或套用公式时某一量(底面积或高)不易求出时,可以转换一下几何体中有关元素的相对位置进行计算求解,该方法尤其适用于求三棱锥的体积. 例 1 在边长为的正方体中,分别是棱、、上的点,且满足(如图 1),试求三棱锥的体积. 分析:若用公式直接计算三棱锥的体积,则需要求出的面积和该三棱锥的高,这两者显然都不易求出,但若将三棱锥的顶点和底面转换一下,变为求三棱锥的体积,便能很容易的求出其高和底面的面积,从而代入公式求解. 解: . 评注:转换顶点和底面是求三棱锥体积的一种常用方法,也是以后学习求点到平面距离的一个理论依据. 二、分割法 分割法也是体积计算中的一...