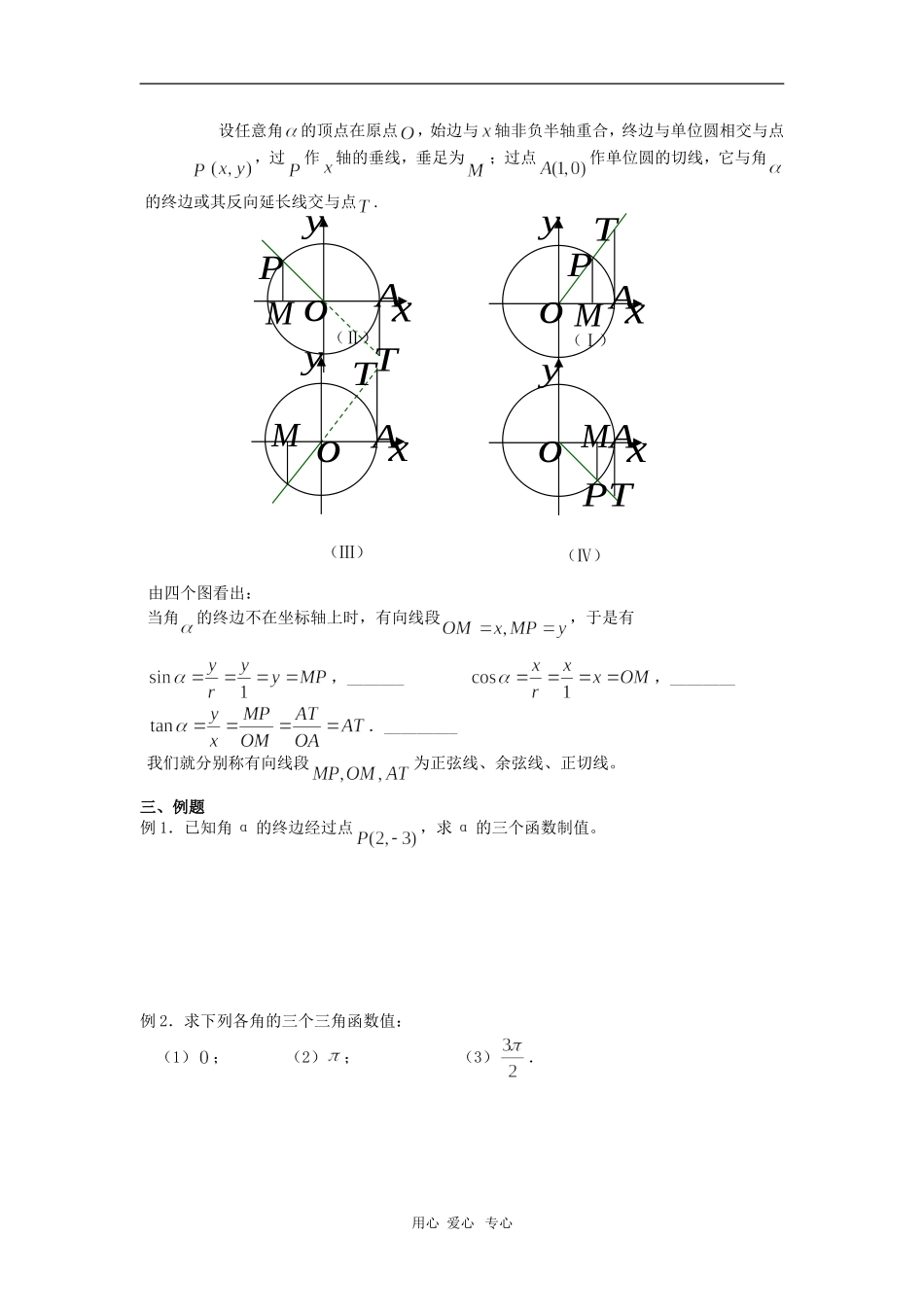
1.2.1 任意角的三角函数一、复习:1、初中锐角的三角函数______________________________________________________2、在 Rt△ABC 中,设 A 对边为 a,B 对边为 b,C 对边为 c,锐角 A 的正弦、余弦、正切依次为_______________________________________________二、新课:1.三角函数定义在直角坐标系中,设 α 是一个任意角,α 终边上任意一点 (除了原点)的坐标为,它与原点的距离为,那么(1)比值_______叫做 α 的正弦,记作_______,即________(2)比值_______叫做 α 的余弦,记作_______,即_________(3)比值_______叫做 α 的正切,记作_______,即_________;2.三角函数的定义域、值域3.三角函数的符号由三角函数的定义,以及各象限内点的坐标的符号,我们可以得知:① 正弦值对于第一、二象限为_____(),对于第三、四象限为____();② 余弦值对于第一、四象限为_____(),对于第二、三象限为____();③ 正切值对于第一、三象限为_______(同号),对于第二、四象限为______(异号).4.诱导公式由三角函数的定义,就可知道:__________________________即有:_________________________ _________________________ _________________________5.当角的终边上一点的坐标满足_______________时,有三角函数正弦、余弦、正切值的几何表示——三角函数线。用心 爱心 专心函 数定 义 域值 域设任意角的顶点在原点,始边与轴非负半轴重合,终边与单位圆相交与点,过作轴的垂线,垂足为;过点作单位圆的切线,它与角的终边或其反向延长线交与点.由四个图看出:当角的终边不在坐标轴上时,有向线段,于是有,_______ ,________._________我们就分别称有向线段为正弦线、余弦线、正切线。三、例题例 1.已知角 α 的终边经过点,求 α 的三个函数制值。例 2.求下列各角的三个三角函数值:(1); (2); (3). 用心 爱心 专心oxyMTPAoxyMTPAxyo MTPAxyoMTA(Ⅳ)(Ⅱ)(Ⅰ)(Ⅲ)例 3.已知角 α 的终边过点,求 α 的三个三角函数值。例 4. 求函数的值域例 5..利用三角函数线比较下列各组数的大小:1 与 2 tan与 tan 四、小结用心 爱心 专心用心 爱心 专心