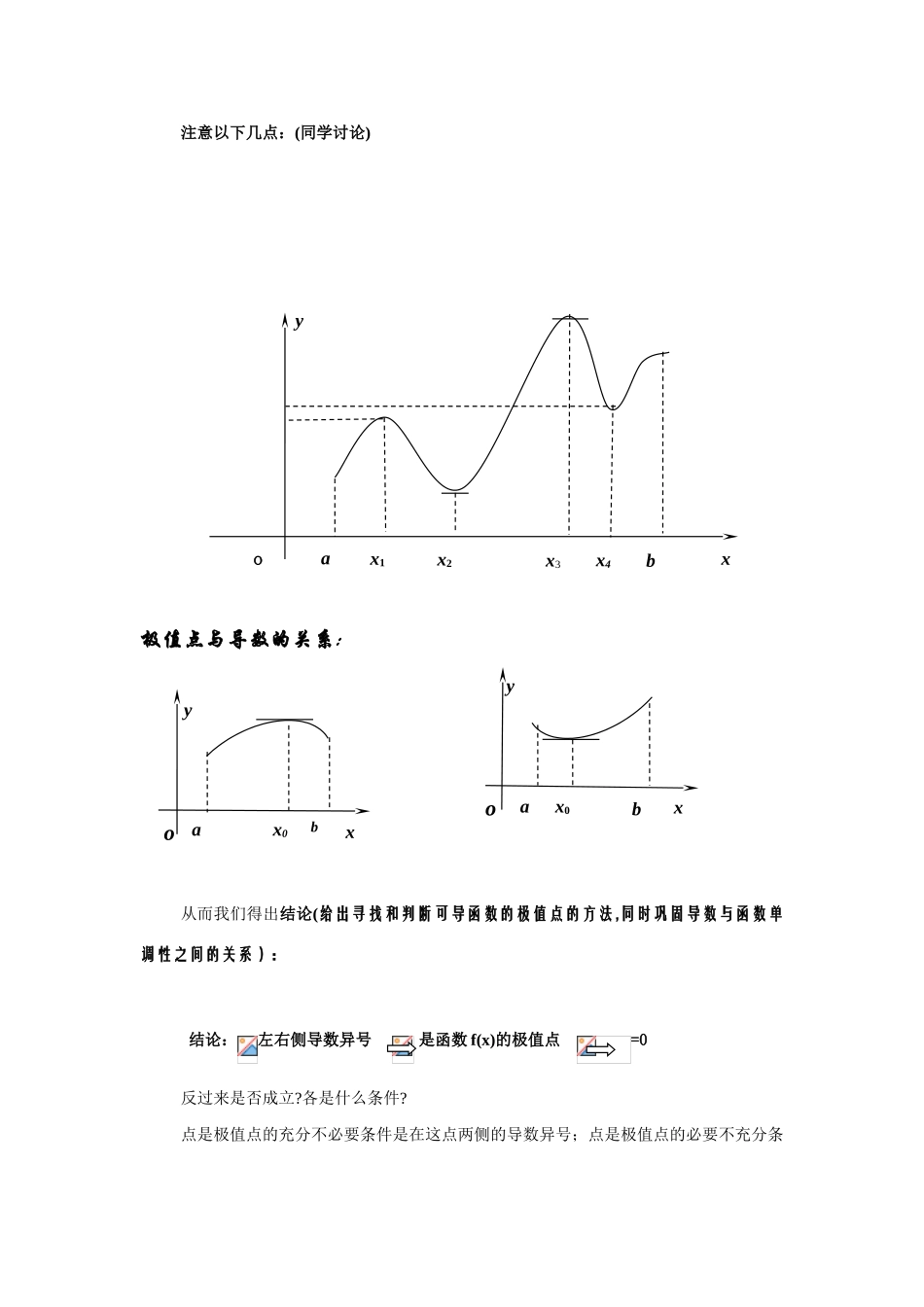
§3.3.2 函数的极值与导数学案学习目标:1.理解极大值、极小值的概念;2.能够运用判别极大值、极小值的方法来求函数的极值;3.掌握求可导函数的极值的步骤;学习重点:极大、极小值的概念和判别方法,以及求可导函数的极值的步骤.学习过程:情景:新课学习一、导入新课观察下图中 P 点附近图像从左到右的变化趋势、P 点的函数值以及点 P 位置的特点二、感性认识运动员的运动过程,体会函数极值的定义.三、数学建构极值点的定义: 3.3-83.3-9x02yoax1x2x34bxyP(x1,f(x1))y=f(x)Q(x2,f(x2))oax0bxyoa x0bxyoax1x2x3x4bxy注意以下几点:(同学讨论)极值点与导数的关系:从而我们得出结论(给出寻找和判断可导函数的极值点的方法,同时巩固导数与函数单调性之间的关系):结论:左右侧导数异号 是函数 f(x)的极值点 =0 反过来是否成立?各是什么条件?点是极值点的充分不必要条件是在这点两侧的导数异号;点是极值点的必要不充分条oxy件是在这点的导数为 0.学生活动 函数 y=f(x)的导数 y/与函数值和极值之间的关系为( )A、导数 y/由负变正,则函数 y 由减变为增,且有极大值B、导数 y/由负变正,则函数 y 由增变为减,且有极大值C、导数 y/由正变负,则函数 y 由增变为减,且有极小值D、导数 y/由正变负,则函数 y 由增变为减,且有极大值四、数学应用 例 1.(课本例 4)求的极值 解:课堂训练:求下列函数的极值 让学生讨论总结求可导函数的极值的基本步骤与方法:一般地,如果函数在某个区间有导数,可以用下面方法求它的极值:① ; ② ③ ④ 强调:要想知道 x0 是极大值点还是极小值点就必须判断 f(x0)=0 左右侧导数的符号例题 2(案例分析)函数 在 x=1 时有极值10,则a,b的值为( )A、 或 B、 或C、 D、 以上都不对 注意:f/(x0)=0是函数取得极值的必要不充分条件练习: 庖丁解牛篇(感受高考)1、(2006 年天津卷)函数的定义域为开区间,导函数在内的图象如图所示,则函数在开区间内有极小值点( A )A.1 个 B.2 个 C.3 个D. 4 个注意:数形结合以及原函数与导函数图像的区别2、(2006年北京卷)已知函数在点处取得极大值,其导函数的图象经过点,,如图所示.求:(Ⅰ)的值; (Ⅱ)的值.例 3 求 y=(x2-1)3+1 的极值五:回顾与小结:注意点: abxy)(xfyO abxy)(xfyO六:作业1、课本P 98 习题 3.3:A 组 4,52、思考题极值和最值的区别与联系