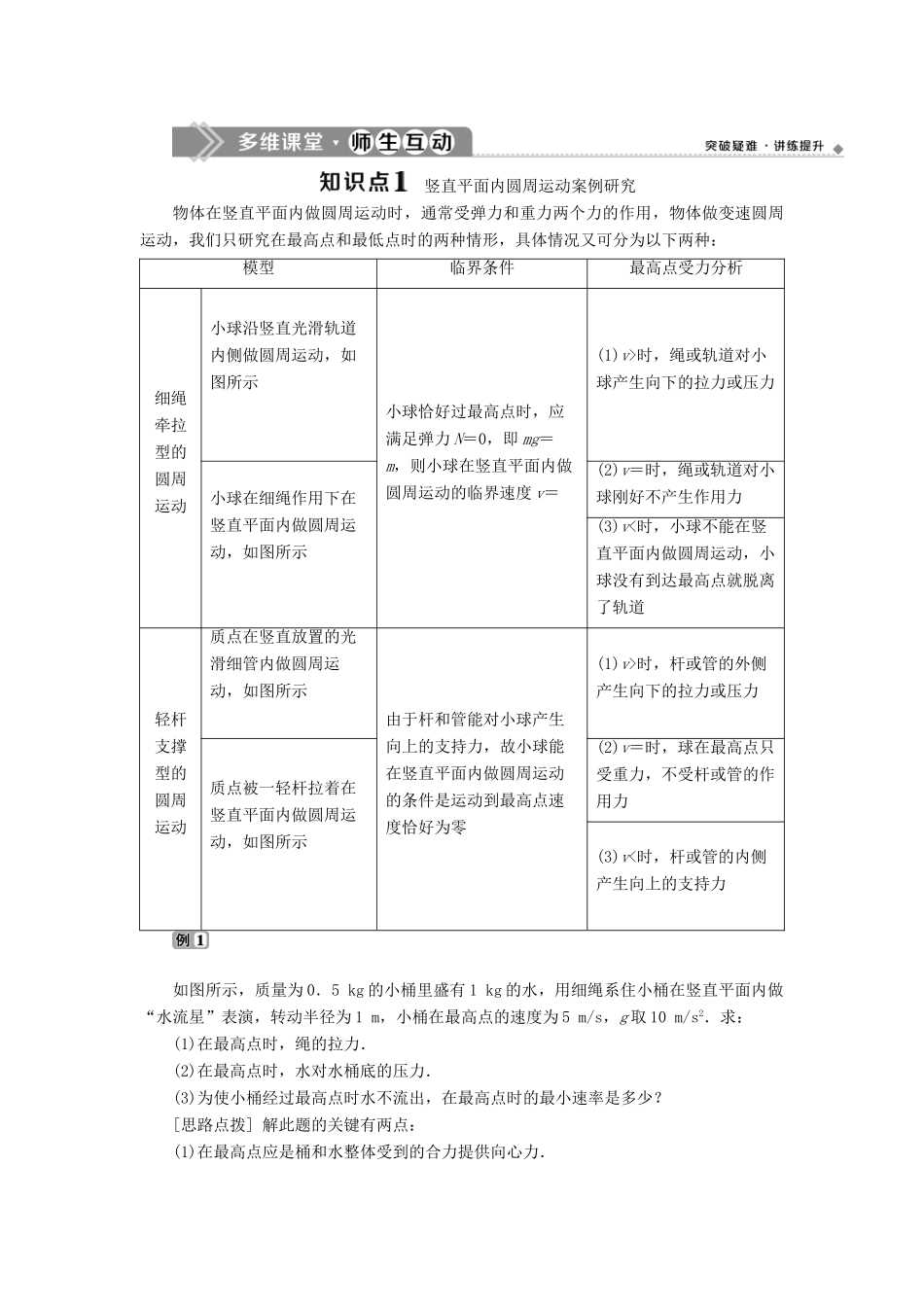
圆周运动的案例分析 1.理解向心力的来源,并能对具体实例进行分析和计算.(重点) 2.掌握牛顿第二定律在圆周运动中的应用.(重点+难点) 3.通过具体分析生活中的圆周运动问题,掌握处理这类问题的思路和方法.一、分析游乐场中的圆周运动1.受力分析(1)过山车在轨道顶部时要受到重力和轨道对车的弹力作用,这两个力的合力提供过山车做圆周运动的向心力.(2)当过山车恰好经过轨道顶部时,弹力为零,此时重力提供向心力.2.临界速度(1)过山车恰好通过轨道顶部时的速度称为临界速度,记作 v 临界,v 临界=.(2)当过山车通过轨道最高点时的速度 v ≥ 时,过山车就不会脱离轨道;当 v> 时,过山车对轨道还会产生压力作用.(3)当过山车通过轨道最高点时的速度 v < 时,过山车就会脱离轨道,不能完成圆周运动.1.为什么过山车在轨道的顶端悬空而没有落下呢?提示:只要过山车在冲向最高点时仍有很高的速度 v,所需要的向心力便会比较大.假如所需的向心力比车的重力大,部分所需的向心力便要由路轨给予过山车的作用力 N 提供,两部分加起来有 mg+N=.此时如果速度 v 越大,过山车与路轨之间的相互作用力也越大,它便越紧贴着路轨,不会掉下来.二、研究运动物体转弯时的向心力1.自行车转弯时要向转弯处的内侧倾斜,由地面对车的作用力与重力的合力作为转弯所需要的向心力.2.汽车在水平路面上转弯时由地面的摩擦力提供向心力.3.火车转弯时的向心力由重力和铁轨对火车的支持力的合力提供,其向心力方向沿水平方向.2.假定你是一个铁路设计的工程师,你打算用什么方法为火车转弯提供向心力?提示:要根据弯道的半径和规定的行驶速度,确定内外轨的高度差,使火车转弯时所需的向心力几乎完全由重力 G 和支持力 N 的合力来提供. 竖直平面内圆周运动案例研究物体在竖直平面内做圆周运动时,通常受弹力和重力两个力的作用,物体做变速圆周运动,我们只研究在最高点和最低点时的两种情形,具体情况又可分为以下两种:模型临界条件最高点受力分析细绳牵拉型的圆周运动小球沿竖直光滑轨道内侧做圆周运动,如图所示小球恰好过最高点时,应满足弹力 N=0,即 mg=m,则小球在竖直平面内做圆周运动的临界速度 v=(1)v>时,绳或轨道对小球产生向下的拉力或压力小球在细绳作用下在竖直平面内做圆周运动,如图所示(2)v=时,绳或轨道对小球刚好不产生作用力(3)v<时,小球不能在竖直平面内做圆周运动,小球没有到达最高点就脱离...