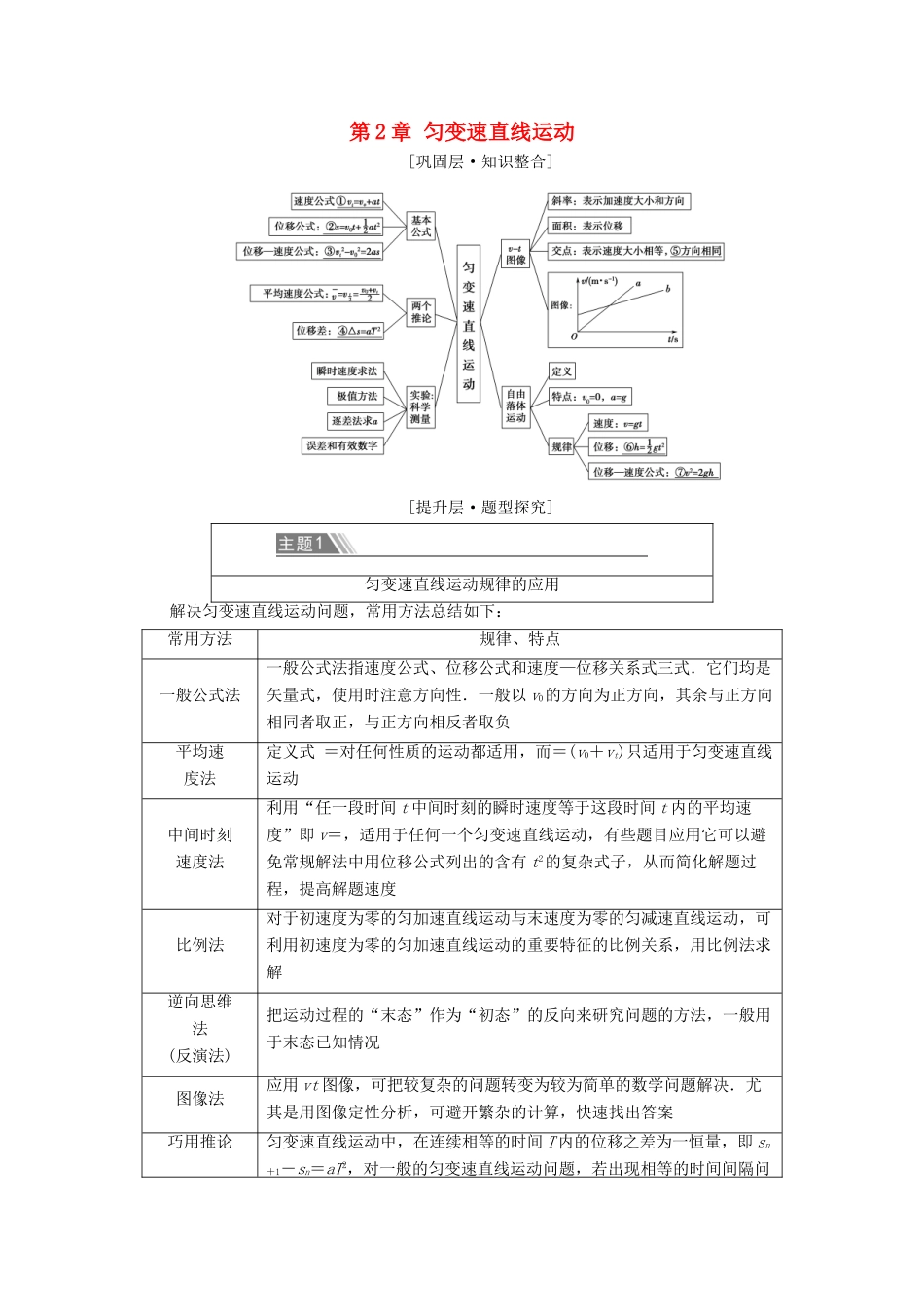
第 2 章 匀变速直线运动[巩固层·知识整合][提升层·题型探究]匀变速直线运动规律的应用解决匀变速直线运动问题,常用方法总结如下:常用方法规律、特点一般公式法一般公式法指速度公式、位移公式和速度—位移关系式三式.它们均是矢量式,使用时注意方向性.一般以 v0的方向为正方向,其余与正方向相同者取正,与正方向相反者取负平均速度法定义式 =对任何性质的运动都适用,而=(v0+vt)只适用于匀变速直线运动中间时刻速度法利用“任一段时间 t 中间时刻的瞬时速度等于这段时间 t 内的平均速度”即 v=,适用于任何一个匀变速直线运动,有些题目应用它可以避免常规解法中用位移公式列出的含有 t2的复杂式子,从而简化解题过程,提高解题速度比例法对于初速度为零的匀加速直线运动与末速度为零的匀减速直线运动,可利用初速度为零的匀加速直线运动的重要特征的比例关系,用比例法求解逆向思维法(反演法)把运动过程的“末态”作为“初态”的反向来研究问题的方法,一般用于末态已知情况图像法应用 vt 图像,可把较复杂的问题转变为较为简单的数学问题解决.尤其是用图像定性分析,可避开繁杂的计算,快速找出答案巧用推论匀变速直线运动中,在连续相等的时间 T 内的位移之差为一恒量,即 sn+1-sn=aT2,对一般的匀变速直线运动问题,若出现相等的时间间隔问Δs=sn+1-sn=aT2解题题,应优先考虑用 Δs=aT2求解巧选参考系解题物体的运动是相对一定的参考系而言的.研究地面上物体的运动常以地面为参考系,有时为了研究问题方便,也可巧妙地选用其他物体为参考系,甚至在分析某些较为复杂的问题时,为了求解简捷,还需灵活地转换参考系【例 1】 物体从静止开始做匀加速直线运动,已知第 2 s 内的位移为 s,则物体运动的加速度大小为多少?(用 s 表示)[解析] 法一用 s=at2求解:设物体的加速度大小为 a,物体在第 2 s 内的位移应等于前 2 s 内的位移与第 1 s 内的位移之差,即s=at-at,代入数据解得 a=s.法二(用 v2-v=2as 求解):设物体的加速度大小为 a,则物体在第 2 s 初的速度 v0=a,第 2 s 末的速度 v=2a,由v2-v=2as,得(2a)2-a2=2as,解得 a=s.法三(用比例法求解):设物体的加速度大小为 a,在第 1 s 内、第 2 s 内的位移大小分别为 s1和 s2,因 s1∶s2=1∶3,又 s2=s,故 s1=s,对第 1 s 内有 s1=a,解得 a=s.法四(用 v=求解):设物体的加速...