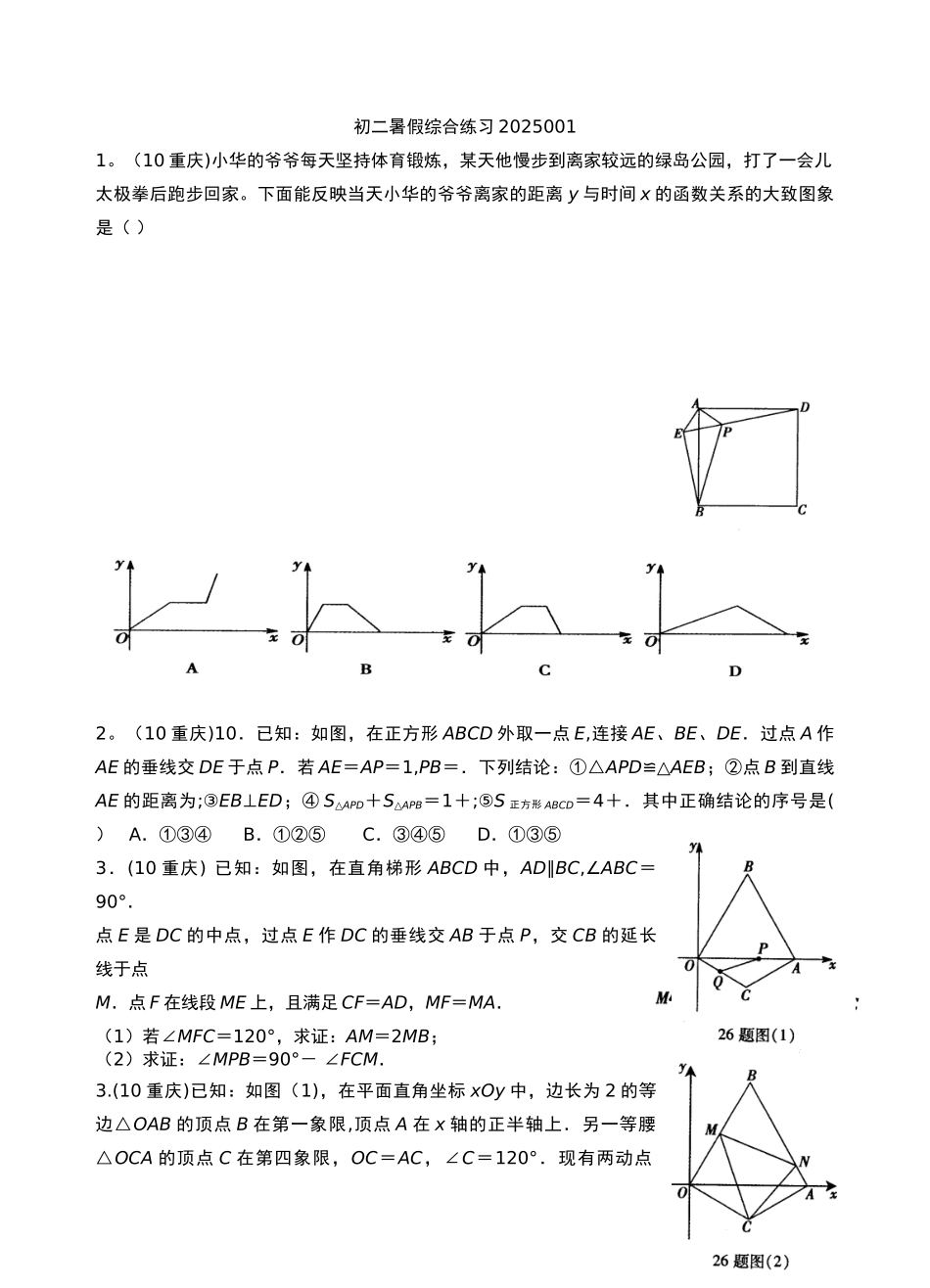
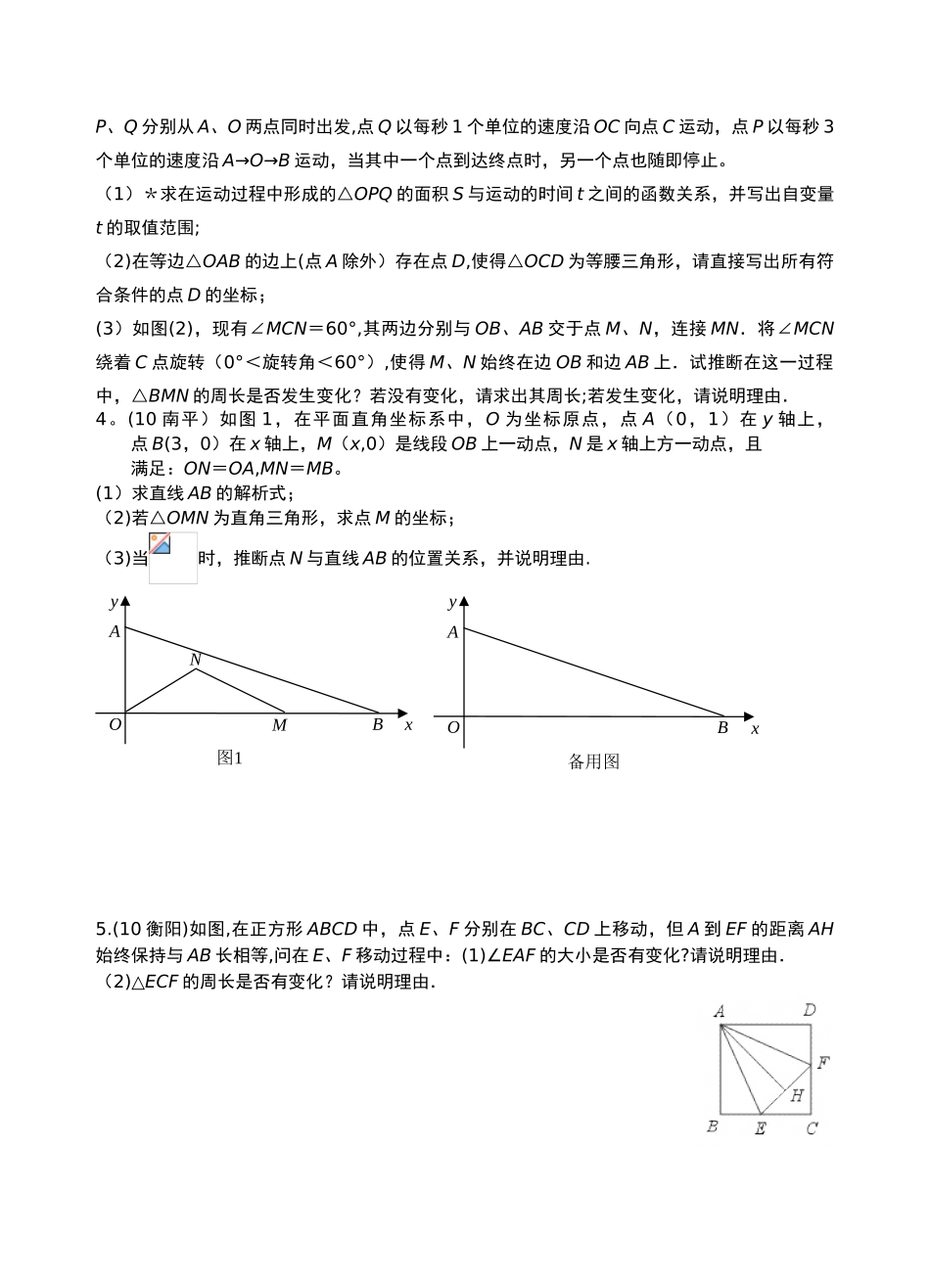
初二暑假综合练习 20250011。(10 重庆)小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家。下面能反映当天小华的爷爷离家的距离 y 与时间 x 的函数关系的大致图象是( )2。(10 重庆)10.已知:如图,在正方形 ABCD 外取一点 E,连接 AE、BE、DE.过点 A 作AE 的垂线交 DE 于点 P.若 AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点 B 到直线AE 的距离为;③EB⊥ED;④ S△APD+S△APB=1+;⑤S 正方形 ABCD=4+.其中正确结论的序号是( ) A.①③④ B.①②⑤ C.③④⑤ D.①③⑤3.(10 重庆) 已知:如图,在直角梯形 ABCD 中,AD∥BC,∠ABC=90°.点 E 是 DC 的中点,过点 E 作 DC 的垂线交 AB 于点 P,交 CB 的延长线于点M.点 F 在线段 ME 上,且满足 CF=AD,MF=MA.(1)若∠MFC=120°,求证:AM=2MB;(2)求证:∠MPB=90°- ∠FCM.3.(10 重庆)已知:如图(1),在平面直角坐标 xOy 中,边长为 2 的等边△OAB 的顶点 B 在第一象限,顶点 A 在 x 轴的正半轴上.另一等腰△OCA 的顶点 C 在第四象限,OC=AC,∠C=120°.现有两动点P、Q 分别从 A、O 两点同时出发,点 Q 以每秒 1 个单位的速度沿 OC 向点 C 运动,点 P 以每秒 3个单位的速度沿 A→O→B 运动,当其中一个点到达终点时,另一个点也随即停止。(1)*求在运动过程中形成的△OPQ 的面积 S 与运动的时间 t 之间的函数关系,并写出自变量t 的取值范围;(2)在等边△OAB 的边上(点 A 除外)存在点 D,使得△OCD 为等腰三角形,请直接写出所有符合条件的点 D 的坐标;(3)如图(2),现有∠MCN=60°,其两边分别与 OB、AB 交于点 M、N,连接 MN.将∠MCN绕着 C 点旋转(0°<旋转角<60°),使得 M、N 始终在边 OB 和边 AB 上.试推断在这一过程中,△BMN 的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.4。(10 南平)如图 1,在平面直角坐标系中,O 为坐标原点,点 A(0,1)在 y 轴上,点 B(3,0)在 x 轴上,M(x,0)是线段 OB 上一动点,N 是 x 轴上方一动点,且满足:ON=OA,MN=MB。(1)求直线 AB 的解析式; (2)若△OMN 为直角三角形,求点 M 的坐标;(3)当时,推断点 N 与直线 AB 的位置关系,并说明理由.5.(10 衡阳)如图,在正方形 ABCD 中,点 E、F ...