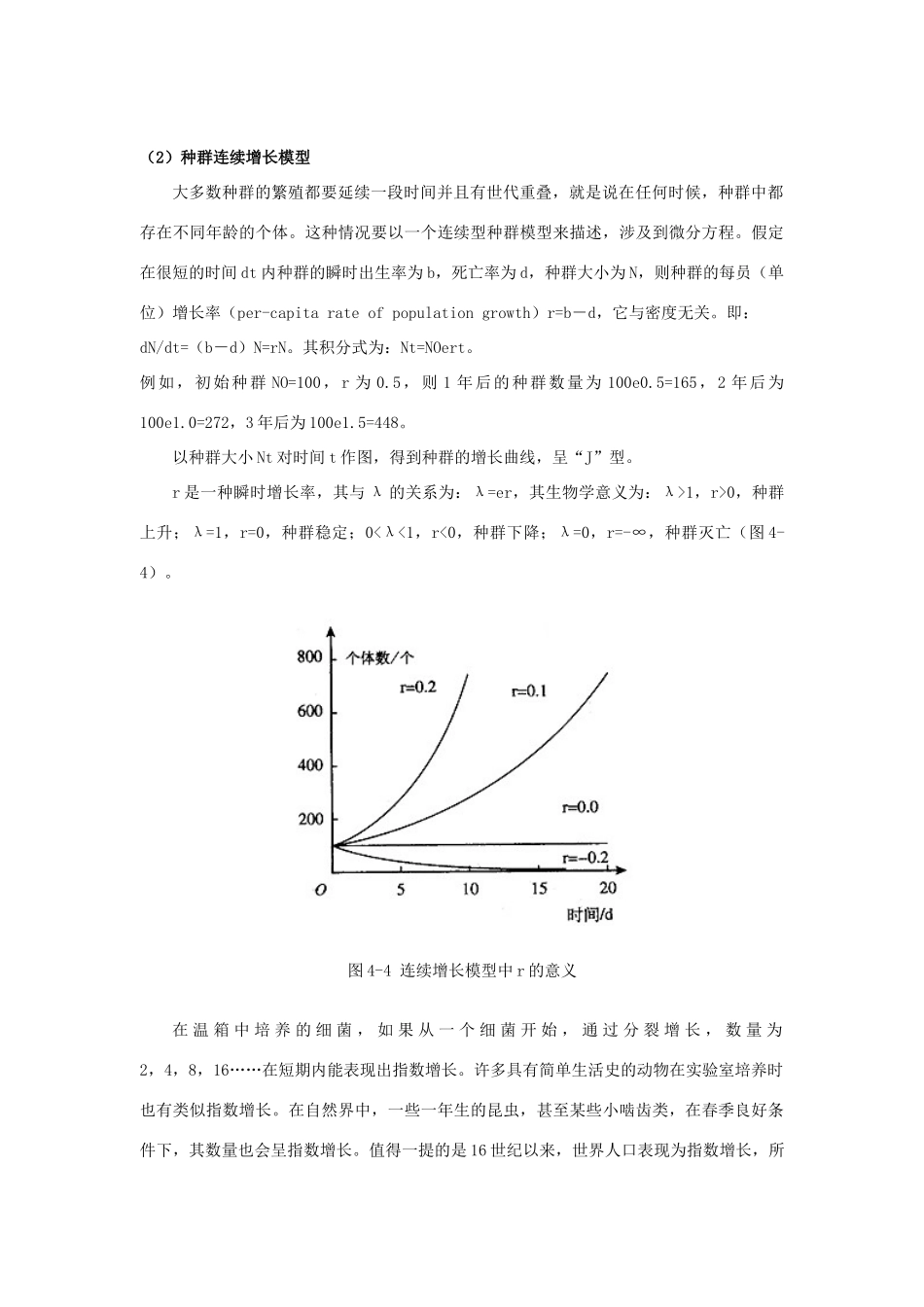
《种群数量的变动》1.在理想状态下的种群增长种群在“无限”的环境中,即假定环境中空间、食物等资源是无限的,因而其增长率不随种群本身的密度而变化,这类增长通常呈指数增长,可称为与密度无关的增长,又称为“J”型增长。与密度无关的增长又可分为两类:如果种群的各个世代彼此不相重叠,例如,一年生植物和许多一年生殖一次的昆虫,其增长是不连续的、分步的,称为离散增长,一般用差分方程描述;如果种群的各个世代彼此重叠(如人和多数兽类),其种群增长是连续的,可用微分方程描述。(1)种群离散增长模型最简单的单种种群增长的数学模型,通常是把世代 t+1 的种群 Nt+1 与世代 t 的种群 Nt联系起来的差分方程:Nt+1=λNt 或 Nt=Noλt(N 为种群的大小,t 为时间,λ 为种群的周限增长率)。例如,一年生生物(即世代间隔为一年)种群,开始时 10 个雌体,到第二年成为 200个,那就是说,NO=10,N1=200,即一年增长 20 倍,以 λ 代表两个世代的比率:λ=N1/N0=20。如 果 种 群 在 无 限 的 环 境 下 以 这 个 速 度 年 复 一 年 地 增 长 , 其 种 群 数 量 为10,10×201,10×202,10×203,…,Nt=NOλt。λ 是种群离散增长模型中有具体意义的参数,其生物学意义为(图 4-2):λ>1,种群数量上升;λ=1,种群数量稳定;0<λ<1,种群数量下降;λ=0,雌体没有繁殖,种群在下一代中灭亡。图 4-2 λ 值的生物学意义图解无论是在实验室还是在田间观察都能发现,很多种群在一个新环境定居或通过了瓶颈(bottle neck)期以后,其种群增长形式很像是几何级数增长。例如,在 20 世纪 30 年代曾将环颈雉引入美国华盛顿州海岸附近的一个岛屿,此后环颈雉种群的增长如图 4-3 所示:最初几年种群增长很慢,到 40 年代时种群增长加快,由于环颈雉是一种经济狩猎鸟类,所以种群的增长受到了限制,但在此之前的增长形式很像是 λ=1.46 的几何级数增长模型,其理论曲线就是图中的虚线。环颈雉种群是从 1937 年的 50 只开始增长的,应当注意的是,环颈雉的越冬死亡率降低了每年春季所观察到的种群数量(低于前一年秋季的个体数量),结果使种群的增长曲线呈“Z”型(图 4-3)。图 4-3 20 世纪 30 年代美国某岛屿环颈雉种群增长图(2)种群连续增长模型大多数种群的繁殖都要延续一段时间并且有世代重叠,就是说在任何时候,种群中都存在不同年龄的个体。这种情况要以一个连...