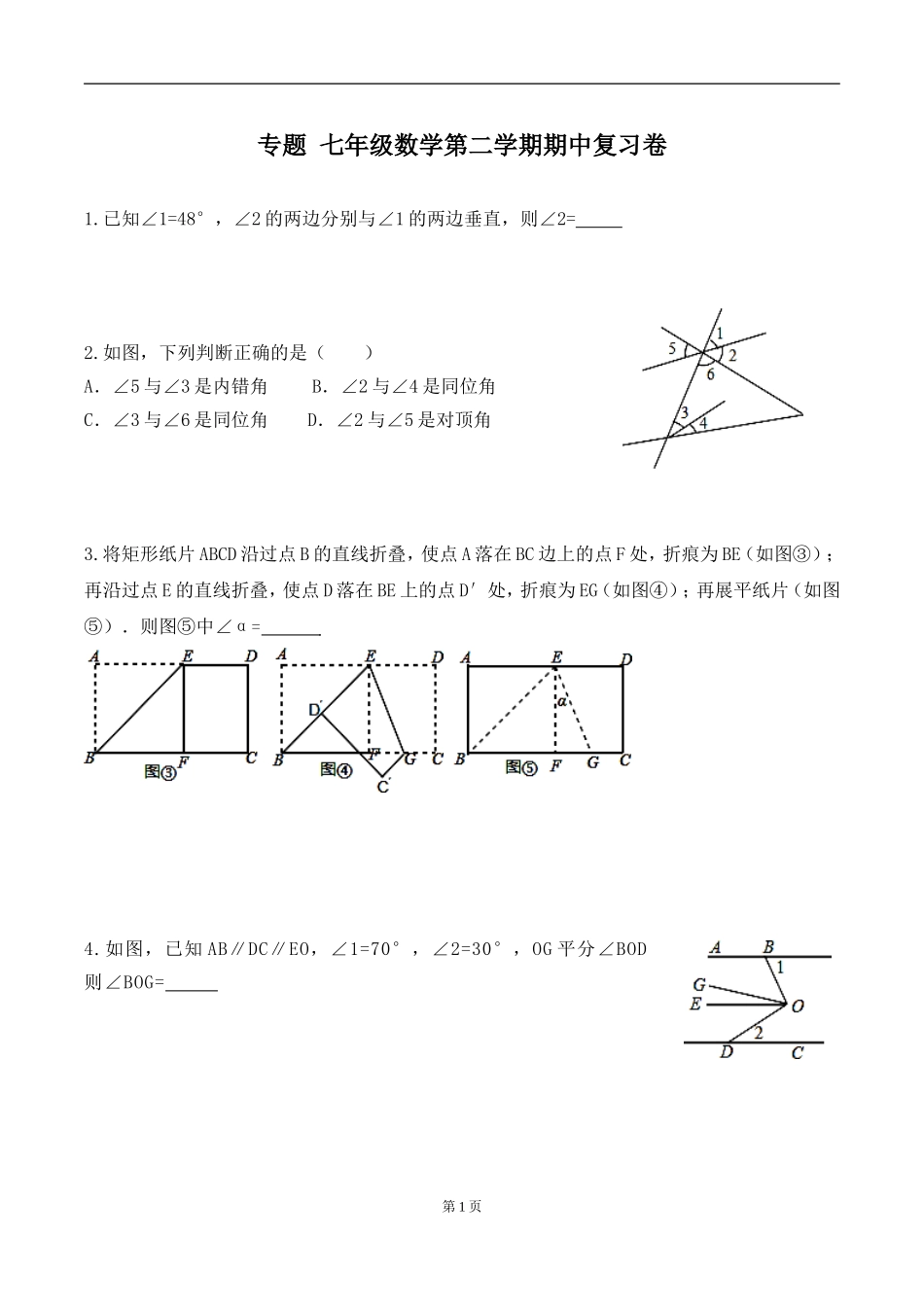
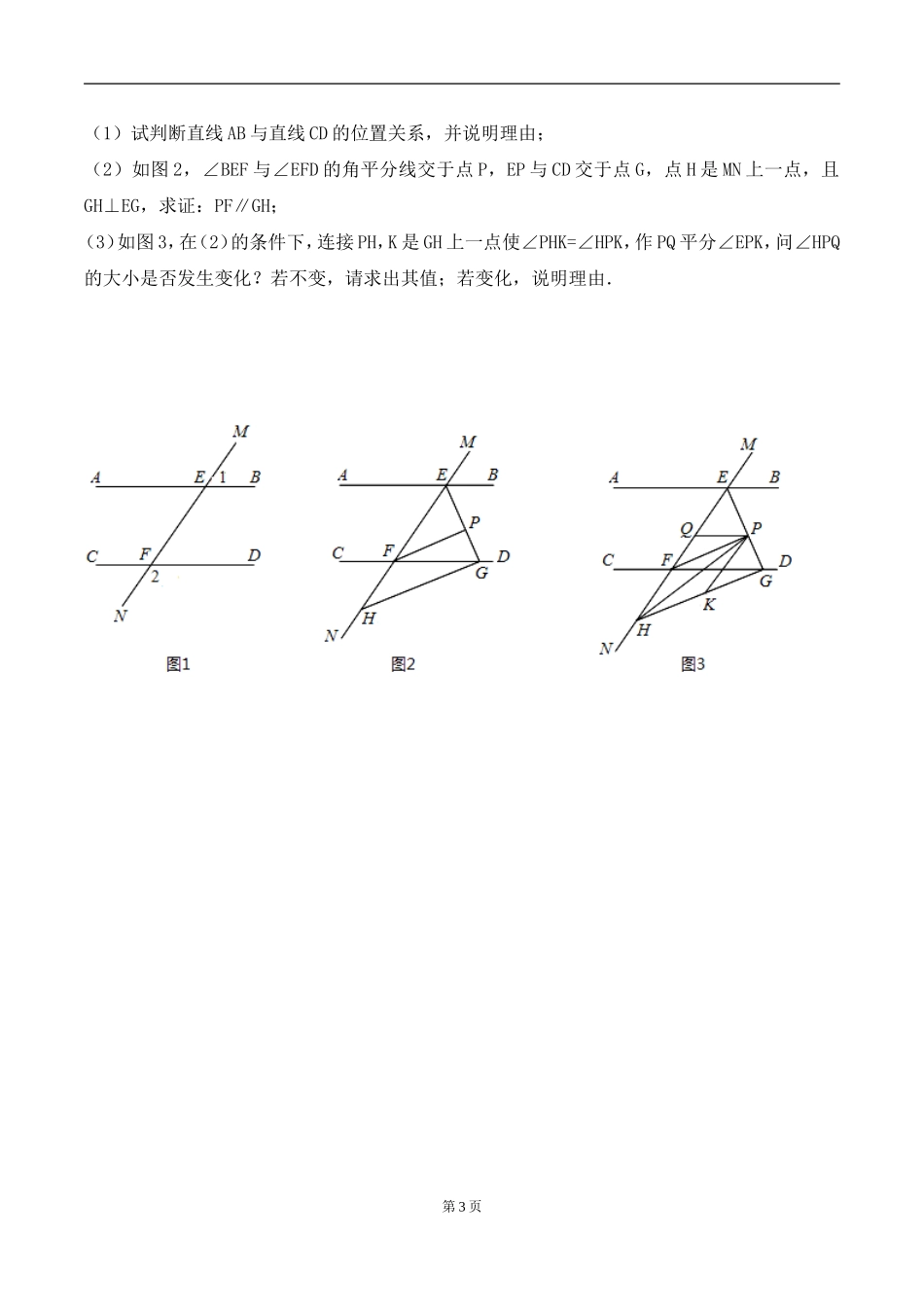
专题 七年级数学第二学期期中复习卷1.已知∠1=48°,∠2 的两边分别与∠1 的两边垂直,则∠2= 2.如图,下列判断正确的是( )A.∠5 与∠3 是内错角 B.∠2 与∠4 是同位角C.∠3 与∠6 是同位角 D.∠2 与∠5 是对顶角3.将矩形纸片 ABCD 沿过点 B 的直线折叠,使点 A 落在 BC 边上的点 F 处,折痕为 BE(如图③);再沿过点 E 的直线折叠,使点 D 落在 BE 上的点 D′处,折痕为 EG(如图④);再展平纸片(如图⑤).则图⑤中∠α= 4.如图,已知 AB∥DC∥EO,∠1=70°,∠2=30°,OG 平分∠BOD则∠BOG= 第 1 页5.已知:如图,AB∥EF,BC⊥CD,则∠α、∠β、∠γ 之间的关系是( )A.∠α-∠β+∠γ=90°B.∠α+∠β-∠γ=90°C.∠α-∠β+∠γ=180° D.∠β+∠γ-∠α=906.将一副直角三角板如图放置,使含 30°角的三角板的直角边和含 45°角的三角板的一条直角边重合,则∠1 的度数为 7.如图:在直角坐标系中,第一次将△AOB 变换成△OA1B1,第二次将三角形变换成△OA2B2,第三次将△OA2B2,变换成△OA3B3,已知 A(1,3),A1(3,3),A2(5,3),A3(7,3);B(2,0),B1(4,0 ),B 2 (8,0),B 3(16,0).(1)观察每次变换前后的三角形有何变化,找出规律,按此变化规律再将△OA3B3 变换成△OA4B4,则 A4的坐标是 ,B4的坐标是 (2)若按(1)找到的规律将△OAB 进行了 n 次变换,得到△OAnBn,比较每次变换中三角形顶点有何变化,找出规律,推测 An的坐标是 ,B n 的坐标是 .8.如图 1,直线 MN 与直线 AB、CD 分别交于点 E、F,∠1 与∠2 互补.第 2 页(1)试判断直线 AB 与直线 CD 的位置关系,并说明理由;(2)如图 2,∠BEF 与∠EFD 的角平分线交于点 P,EP 与 CD 交于点 G,点 H 是 MN 上一点,且GH⊥EG,求证:PF∥GH;(3)如图 3,在(2)的条件下,连接 PH,K 是 GH 上一点使∠PHK=∠HPK,作 PQ 平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.第 3 页9.如图 1,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且.(1)求的值;(2)①在 x 轴的正半轴上存在一点 M,使,求出点 M 的坐标;② 在坐标轴的其它位置是否存在点 M,使仍然成立?若存在,请直接写出符合条件的点 M 的坐标;(3)如图 2,过点 C 作 CD⊥y 轴交 y 轴于点 D,点 P ...