（河北专版）秋八年级数学上册 第十二章 全等三角形 专题训练（三）有关全等三角形的开放、探究题作业课件 （新版）新人教版-（新版）新人教版初中八年级上册数学课件VIP专享

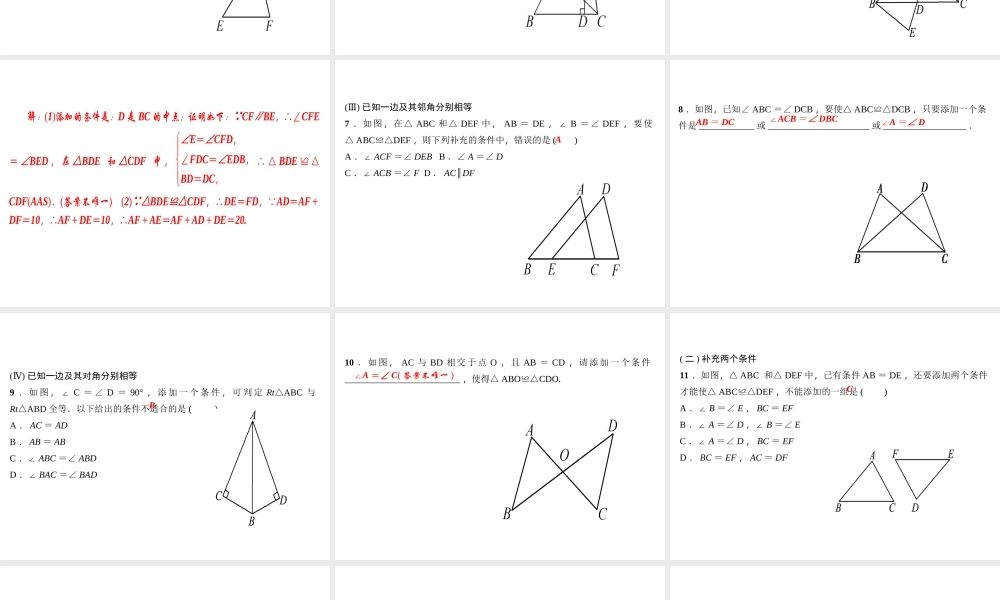
第十二章 全等三角形人教版专题训练 ( 三 ) 有关全等三角形的开放、探究题类型一：条件开放型( 一 ) 补充一个条件( )Ⅰ 已知两边分别相等1 ．如图， AB ＝ DB ， BC ＝ BE ，欲证△ ABEDBC≌△，则需补充的条件是 ( )A ．∠ A ＝∠ D B ．∠ E ＝∠ CC ．∠ A ＝∠ C D ．∠ 1 ＝∠ 2D2 ．如图，已知 AC ＝ BD ，判定△ ABCDCB≌△还需增加的条件是__________________________________ ．AB ＝ CD( 答案不唯一 )( )Ⅱ 已知两角分别相等3 ．如图，已知∠ A ＝∠ D ，∠ 1 ＝∠ 2 ，那么要得到△ ABCDEF≌△，还应给出的条件是 ( )A ．∠ E ＝∠ B B ． ED ＝ BCC ． AB ＝ EF D ． AF ＝ CDD4 ． (2017· 黑 龙 江 ) 如 图 ， BC EF∥， AC DF∥， 添 加 一 个 条 件________________________________________________________________ ，使得△ ABCDEF.≌△AB ＝ DE 或 BC ＝ EF 或 AC ＝ DF 或 AD ＝ BE( 只需添加一个即可 )5 ． (2016· 济宁 ) 如图，△ ABC 中， ADBC⊥， CEAB⊥，垂足分别为点D ， E ， AD ， CE 交 于 点 H ， 请 你 添 加 一 个 适 当 的 条 件 ：___________________ ，使△ AEHCEB.≌△AH ＝ CB( 答案不唯一 )6 ．如图，在△ ABC 中， D 是 BC 边上的点 ( 不与 B ， C 重合 ) ， F ， E 分别 是 AD 及 其 延 长 线 上 的 点 ， CF BE. ∥请 你 添 加 一 个 条 件 ， 使△ BDECDF (≌△不再添加其他线段，不再标注或使用其他字母 ) ，并给出证明．(1) 你添加的条件是： ______________ ，并证明△ BDECDF≌△；(2) 若 AD ＝ 10 ，求 AF ＋ AE 的长．解：(1)添加的条件是：D 是 BC 的中点；证明如下： CF∥BE，∴∠CFE＝ ∠BED ， 在 △BDE 和 △CDF 中 ，∠E＝∠CFD，∠FDC＝∠EDB，BD＝DC，∴ △ BDE ≌ △CDF(AAS)．(答案不唯一) (2) △BDE≌△CDF，∴DE＝FD， AD＝AF＋DF＝10，∴AF＋DE＝10，∴AF＋AE＝AF＋AD＋DE＝20. ()Ⅲ 已知一边及其邻角分别相等7 ．如图，在△ ABC 和△ DEF 中， AB ＝ DE ，∠ B ＝∠ DEF ，要使△ ABCDEF≌△，则下列补充的条件中，错误的是 ( )A ．∠ ACF ＝∠ DEB B ．∠ A ＝∠ DC ．∠ ACB ＝...