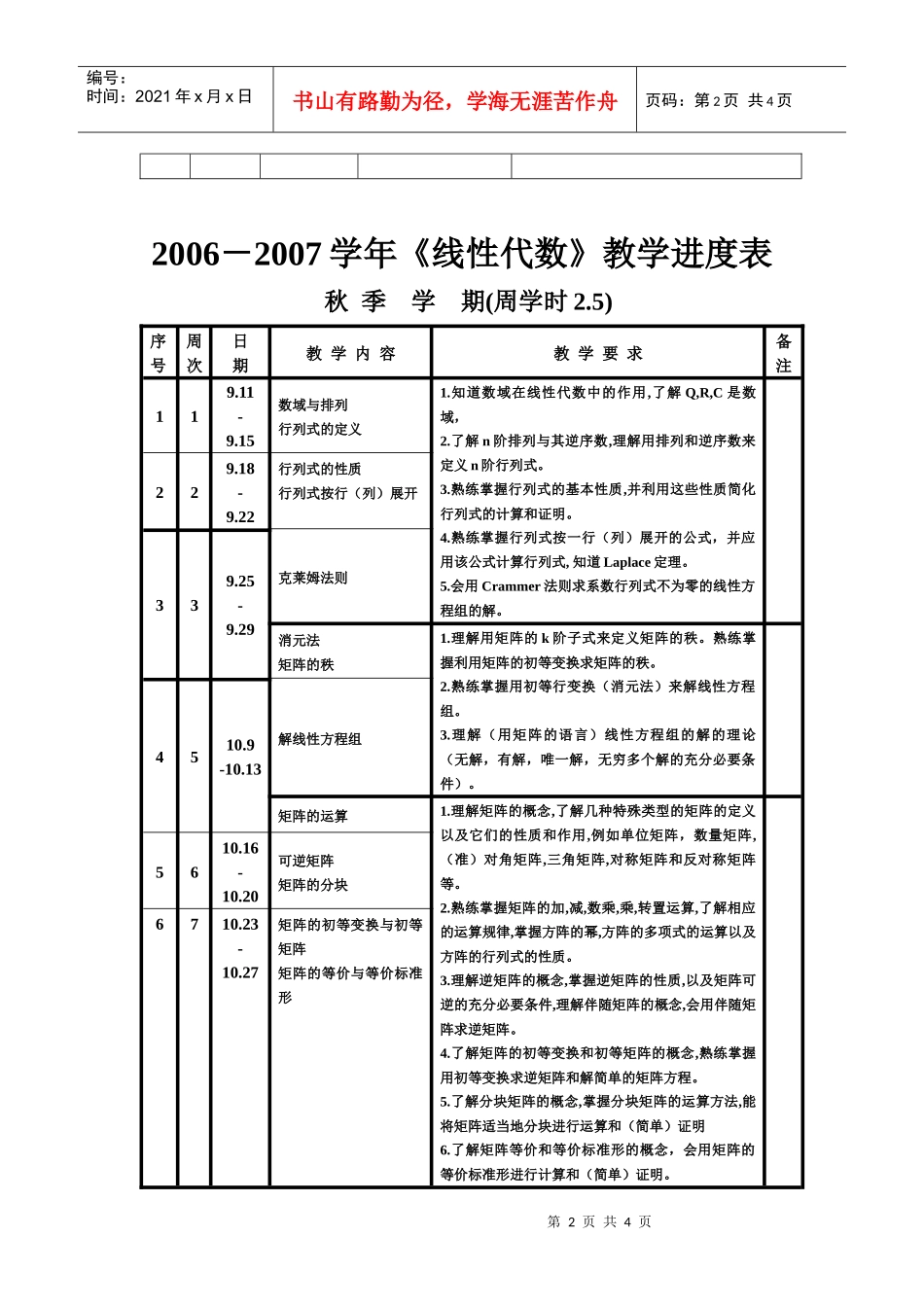
第1页共4页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第1页共4页通知____各位_______老师:根据校教务部的有关通知精神,2006--2007学年第1,2学期线性代数答疑时间安排如下,届时请你前往紫金港校区答疑。此致敬礼!数学系2006年2月20日春季学期(线性代数)教师答疑时间安排表序号周次周六上午答疑教师备注119月16日答疑地点:东1B2楼207教师休息室(有空调)答疑时间:8:30---10:50229月23日陈明飞叶兴德339月30日国庆换课4410月7日国庆停课5510月14日汪国军,薛儒英6610月21日运动会停课7710月28日单鉴华,汤树元8811月4日夏巧玲,龚乐春9911月18日停课考试夏季学期(线性代数)教师答疑时间安排表序号周次周六上午答疑教师备注1111月25日张希,盛为民答疑地点:东1B2楼207教师休息室(有空调)答疑时间:8:30---10:502212月2日葛根年,张国川3312月9日陈明飞叶兴德4412月16日汪国军,薛儒英5512月23日单鉴华,汤树元6612月30日夏巧玲,龚乐春771月6日张希,盛为民881月13日葛根年,张国川991月20日停课考试第2页共4页第1页共4页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第2页共4页2006-2007学年《线性代数》教学进度表秋季学期(周学时2.5)序号周次日期教学内容教学要求备注119.11-9.15数域与排列行列式的定义1.知道数域在线性代数中的作用,了解Q,R,C是数域,2.了解n阶排列与其逆序数,理解用排列和逆序数来定义n阶行列式。3.熟练掌握行列式的基本性质,并利用这些性质简化行列式的计算和证明。4.熟练掌握行列式按一行(列)展开的公式,并应用该公式计算行列式,知道Laplace定理。5.会用Crammer法则求系数行列式不为零的线性方程组的解。229.18-9.22行列式的性质行列式按行(列)展开339.25-9.29克莱姆法则消元法矩阵的秩1.理解用矩阵的k阶子式来定义矩阵的秩。熟练掌握利用矩阵的初等变换求矩阵的秩。2.熟练掌握用初等行变换(消元法)来解线性方程组。3.理解(用矩阵的语言)线性方程组的解的理论(无解,有解,唯一解,无穷多个解的充分必要条件)。4510.9-10.13解线性方程组矩阵的运算1.理解矩阵的概念,了解几种特殊类型的矩阵的定义以及它们的性质和作用,例如单位矩阵,数量矩阵,(准)对角矩阵,三角矩阵,对称矩阵和反对称矩阵等。2.熟练掌握矩阵的加,减,数乘,乘,转置运算,了解相应的运算规律,掌握方阵的幂,方阵的多项式的运算以及方阵的行列式的性质。3.理解逆矩阵的概念,掌握逆矩阵的性质,以及矩阵可逆的充分必要条件,理解伴随矩阵的概念,会用伴随矩阵求逆矩阵。4.了解矩阵的初等变换和初等矩阵的概念,熟练掌握用初等变换求逆矩阵和解简单的矩阵方程。5.了解分块矩阵的概念,掌握分块矩阵的运算方法,能将矩阵适当地分块进行运算和(简单)证明6.了解矩阵等价和等价标准形的概念,会用矩阵的等价标准形进行计算和(简单)证明。5610.16-10.20可逆矩阵矩阵的分块6710.23-10.27矩阵的初等变换与初等矩阵矩阵的等价与等价标准形第3页共4页第2页共4页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第3页共4页线性空间定义与背景向量的线性相关性与无关性向量的极大线性无关组(1)1.理解线性空间的概念,掌握线性空间的性质。2.理解向量的线性组合与线性表示,向量组的线性相关与线性无关的定义。了解并掌握有关向量组的线性相关与线性无关的性质及其判别法。3.理解向量组的极大线性无关组和向量组的秩的概念,掌握求向量组的极大线性无关组和向量组的秩的方法。4.了解向量组等价、理解线性空间的基、维数和向量在一组基下的坐标等概念,掌握基变换和坐标变换公式,会求过渡矩阵。7810.30-11.38911.6-11.9向量的极大线性无关组(2)基和维数91011.13-11.17秋季学期停课考试2005-2006学年《线性代数》教学进度表冬季学期(周学时2.5)序号周次日期教学内容教学要求备注1111.20-11.24子空间矩阵的秩线性方程组解的结构5.了解子空间,会求一组向量生成子空间的基和维数。6.掌握向量组的秩与矩阵的秩之间的关系。熟练掌握齐次线性方程组解空间的维数和系数矩阵秩的关系,根据线性方程组解的结构熟练掌握求线性方程组的解。7.了解欧氏空...