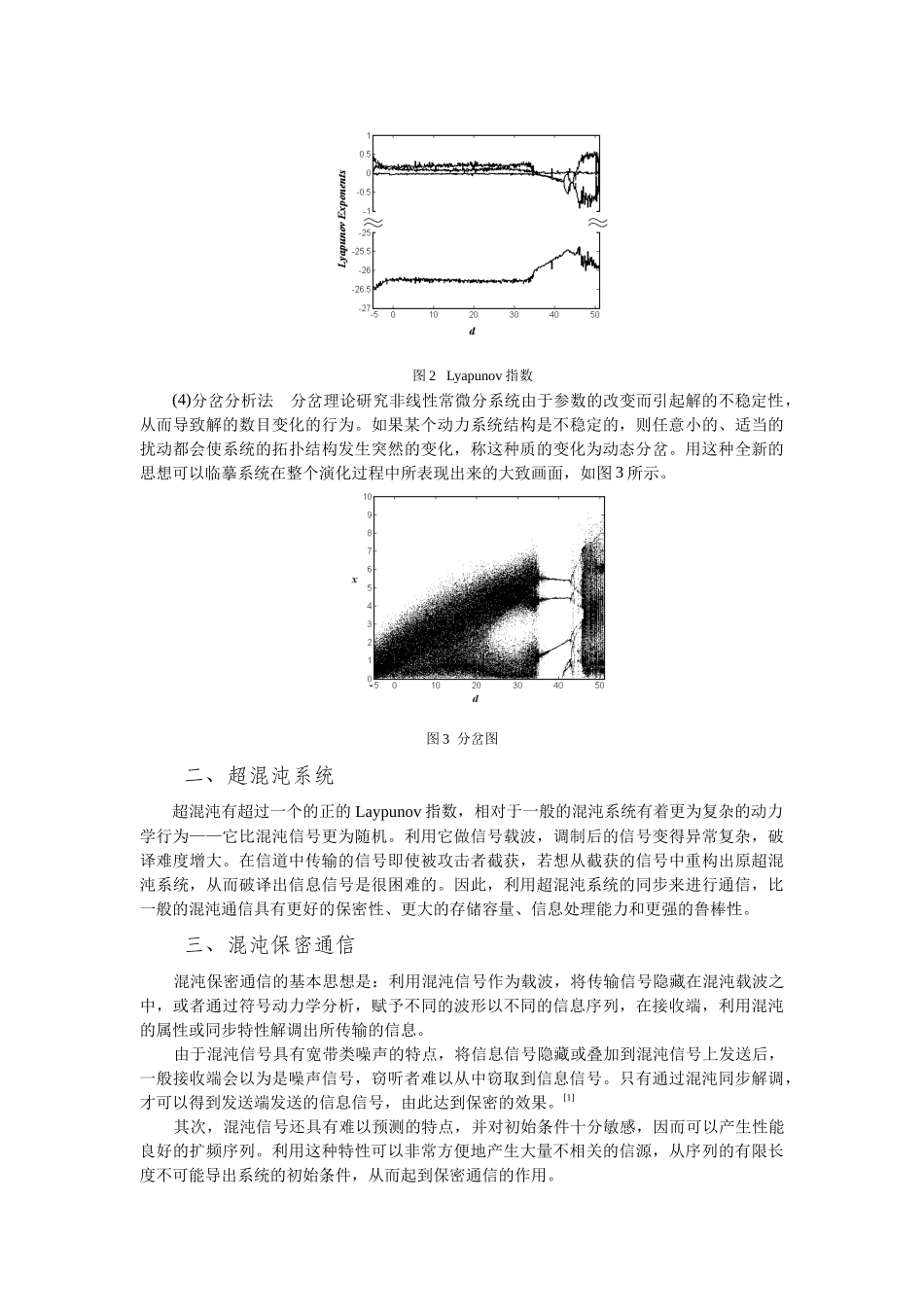
安全与保密基于混沌系统的保密通信研究刘娟(重庆邮电大学通信与信息工程学院重庆400065)摘要:简要介绍了一般混沌系统的概念和特点,以及其超级状态——超混沌系统与一般混沌系统相比的优点;对混沌保密通信进行了介绍,对目前混沌保密通信技术的研究状况进行了综述;最后对进一步需要研究的问题进行了讨论。关键字:混沌超混沌保密通信混沌是二十世纪最重要的科学发现之一,被誉为继相对论和量子力学之后的第三次物理革命。这一理论揭示了有序与无序的统一、确定性与随机性的统一,几乎覆盖了一切科学领域,尤其是在物理学、电子学、力学、数学、经济学、生物学等方面。近年来,混沌理论与保密通信的结合,对通信领域的高科技发展提供了一个新的方向。从2000年开始,国际上对混沌通信研究的步伐越来越快。“现在国际上基于混沌的通信系统的发展己经处于成熟状态,己有几种可能的通信方案被认同和颇具特色”[1],这个鲜明的观点和总体性、方向性的结论更加增强了人们的信心,看到了混沌通信美好的发展前景。一、混沌系统混沌是非线性动力学系统所特有的一种运动形式,是在确定性系统中出现的一种貌似无规则的类随机现象。这里的确定性系统是指混沌系统由确定的动力学方程所描述;随机是指混沌本身具有内在随机性,表现为系统长期行为的不可预测性。同时,必须指出,混沌不等于混乱,它是一种貌似无序的复杂有序现象。混沌的定义很多,比较常用的是R.L.Devaney采用拓扑方法给出的定义。定义1[3]:f:Rn→Rn称为是拓扑传递的,如对任何一对开集U,V⊂Rn,存在k>0,使得fk(U)∩V≠Φ。其中,fk(U)表示迭代k次的函数。这一定义意味着,具有拓扑传递性的动力系统不能被分解为两个在映射下不变的、非交的开集,即不能被细分或不能被分解为两个在f下相互影响的子系统[4]。定义2[3]:f:Rn→Rn有对初始条件的敏感依赖性,如存在δ>0,对任何x∈Rn和x的任何领域N,存在y∈N和自然数n,使得|fn(x)−fn(y)|>δ。定义2表明,具有对初始条件的敏感依赖性的映射,使得至少存在一个任意接近x的点,在f的反复迭代下最终要和x分离至少为δ的距离。定义3[3]:设V为一合集,如果(1)f有对初始条件的敏感依赖性;(2)f是拓扑传递的;(3)周期点在V中稠密。则,f:V→V称为在V上是混沌的。定义3表征了混沌映射的三个要素:不可预测性,不可分解性,包含一定规律性。定义4(连续流的混沌定义)[3]:对于系统˙x=F(x),以x0为初始值的解表示为ϕ(t,x0),ϕ(0,x)=x。记Γ(1)=ϕ(1,x),Γ(2)=ϕ(2,x),⋯,Γ(n)=ϕ(n,x),n∈N,如果Γ(1),Γ(2),⋯,Γ(n),⋯是混沌序列,则系统˙x=F(x)是混沌的。但是,研究混沌运动规律,了解某一系统是否会有混沌运动产生,人们往往不是通过混沌数学定义来确定,而是通过混沌的一般特征去判断、研究。因此,在这里需要描述一下混沌的主要特征。[4](1)对初值的敏感依赖性系统的输出状态为混沌时,即使是以非常微小差别的初始值输入,其输出状态经过有限时间后将会以指数率相互分离。(2)分数维特性奇异吸引只是轨道在相空间中经过无数次的靠近与分离、拉伸与折叠形成的几何图形,具有层次结构的自相似特点。(3)普适性所谓普适性是指不同系统在趋向混沌状态时所表现出来的某些共同特征,它不依具体的系统方程或参数而变。(4)Lyapunov指数的统计特性对非线性映射而言,Lyapunov指数表示n维相空间中运动轨道沿各基向量的平均指数发散率。当Lyapunov指数小于零时,轨道间的距离按指数消失,系统运动状态对应于周期运动或平衡点;当Lyapunov指数大于零时,则在初始状态相邻的轨道按指数分离,系统运动对应于混沌状态;当Lyapunov指数等于零时,各轨道间距离不变,迭代产生的点对应分岔点(即周期加倍的位置)。根据混沌特性可知,判断一个动力学系统是否为混沌系统主要有以下四种方法:[4](1)运动轨迹与相图法根据Matlab的ODE程序进行仿真试验或用Runge-Kutta(龙格库达)法对系统进行仿真试验,可以得到系统的运动轨迹和相平面图,如图1所示。根据相点的运动轨迹或变化情况,可以凭经验对系统的运动特性进行初步判断。但是该方法只能得到初略的定性估计。图1混沌系统相图(2)频谱分析法它的依...