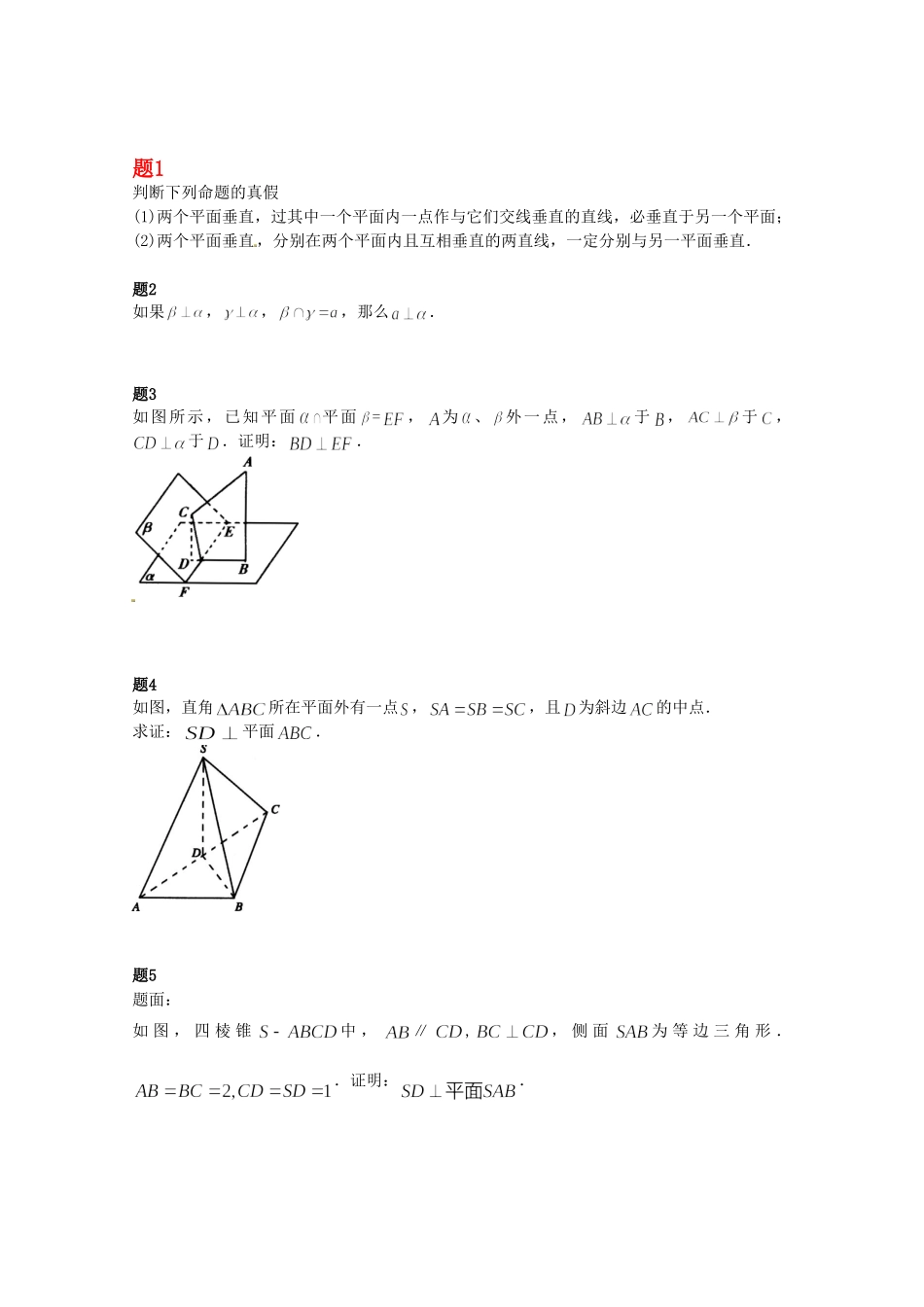
题1判断下列命题的真假(1)两个平面垂直,过其中一个平面内一点作与它们交线垂直的直线,必垂直于另一个平面;(2)两个平面垂直,分别在两个平面内且互相垂直的两直线,一定分别与另一平面垂直.题2如果,,,那么.题3如图所示,已知平面平面=,为、外一点,于,于,于.证明:.题4如图,直角所在平面外有一点,,且为斜边的中点.求证:平面.题5题面:如图,四棱锥中,∥,,侧面为等边三角形..证明:.题6如图,已知正三棱柱的底面边长为2,侧棱长为,点E在侧棱上,点F在侧棱上,且.求证:.题7一个多面体的直观图及三视图如图所示.(其中M、N分别是AF、BC的中点).(1)求证:MN∥平面CDEF;(2)求多面体A—CDEF的体积.题8四棱锥P—ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点.(1)求证:BE∥平面PAD;(2)平面EBD能垂直于平面ABCD吗?为什么?题9如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(1)求证:DE∥平面A1CB;(2)求证:A1F⊥BE;(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.题10平面内有一半圆,直径,过作平面,在半圆上任取一点,连、,且、分别是在、上的射影.(1)求证:;(2)这个图形中有多少个线面垂直关系?(3)这个图形中有多少个直角三角形?(4)这个图形中有多少对相互垂直的直线?课后练习详解题1答案:错误,错误.详解:(1)若该点在两个平面的交线上,则命题是错误的,如图,正方体中,平面平面,平面平面,在上取点,连结,则,即过棱上一点的直线与棱垂直,但与平面不垂直,其错误的原因是没有保证在平面内.可以看出:线在面内这一条件的重要性;(2)该命题注意了直线在平面内,但不能保证这两条直线都与棱垂直,如图,在正方体中,平面平面,平面,平面,且,即与相互垂直,但与平面不垂直.题2答案:见详解.详解:证法一:如图所示,设,,过平面内一点作于,作于. ,∴.又,∴,同理可证. 且,∴.证法二:如图所示,设,在平面内作直线. ,∴.设,在平面内作直线.同理可证,因此.由于,,∴.而,,∴.故由知,.题3答案:见详解.详解: ,,∴.∴、、、四点共面. ,,,∴,.又,∴平面.∴.题4答案:见详解.详解: ,为中点∴即又,∴≌≌∴.即,,∴平面.题5答案:见详解.详解:证明:取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2.连结SE,则又SD=1,故所以为直角.由,得,所以.SD与两条相交直线AB、SE都垂直.所以题6答案:见详解.详解:由已知可得于是有,所以,又,所以平面,则题7答案:(1)见详解;(2).详解:由三视图知该多面体是底面为直角三角形的直三棱柱ADE—BCF,且AB=BC=BF=2,DE=CF=2,∠CBF=90°.(1)取BF的中点G,连结MG、NG,由M、N分别为AF、BC中点,可得NG∥CF,MG∥EF⇒面MNG∥面CDEF⇒MN∥面CDEF.(2)取DE中点为H,连结AH,因为AD=AE⇒AH⊥DE.在直三棱柱ADE—BCF中,平面ADE⊥平面CDEF,面ADE∩面CDEF=DE⇒AH⊥平面CDEF⇒多面体A—CDEF是以AH为高,以矩形CDEF为底面的棱锥,在△ADE中,AH=,SCDEF=DE·EF=4⇒棱锥A—CDEF的体积V=SCDEF·AH=.题8答案:见详解.详解:(1)如图所示,取PD的中点F,连接EF,易证四边形ABEF是平行四边形,∴BE∥AF.又BE⊄平面PAD,AF⊂平面PAD,∴BE∥平面PAD.(2)平面EBD不能垂直于平面ABCD,理由如下:假设平面EBD⊥底面ABCD,过E作EO⊥BD于O,连接AO,CO,由于A,O,C是P,E,C三点在平面ABCD上的射影,P,E,C三点均在直线PC上,故它们的射影也共线. 平面EBD⊥平面ABCD,EO⊂平面EBD,EO⊥BD,BD=平面EBD∩平面ABCD,∴EO⊥平面ABCD,又PA⊥平面ABCD,∴EO∥PA,而E为PC的中点,∴O为AC的中点,又由AB∥CD,可知△ABO∽△CDO,且相似比为1∶1,∴AB=CD,这与“四边形ABCD为梯形”矛盾,故假设不成立,从而平面EBD不能垂直于平面ABCD.题9答案:见详解.详解:(1)因为D,E分别为AC,AB的中点,所以DE∥BC.又因为DE平面A1CB,所以DE∥平面A1CB.(2)由已知得AC⊥BC且DE∥BC,所以DE⊥AC.所以DE⊥A1D,DE⊥C...