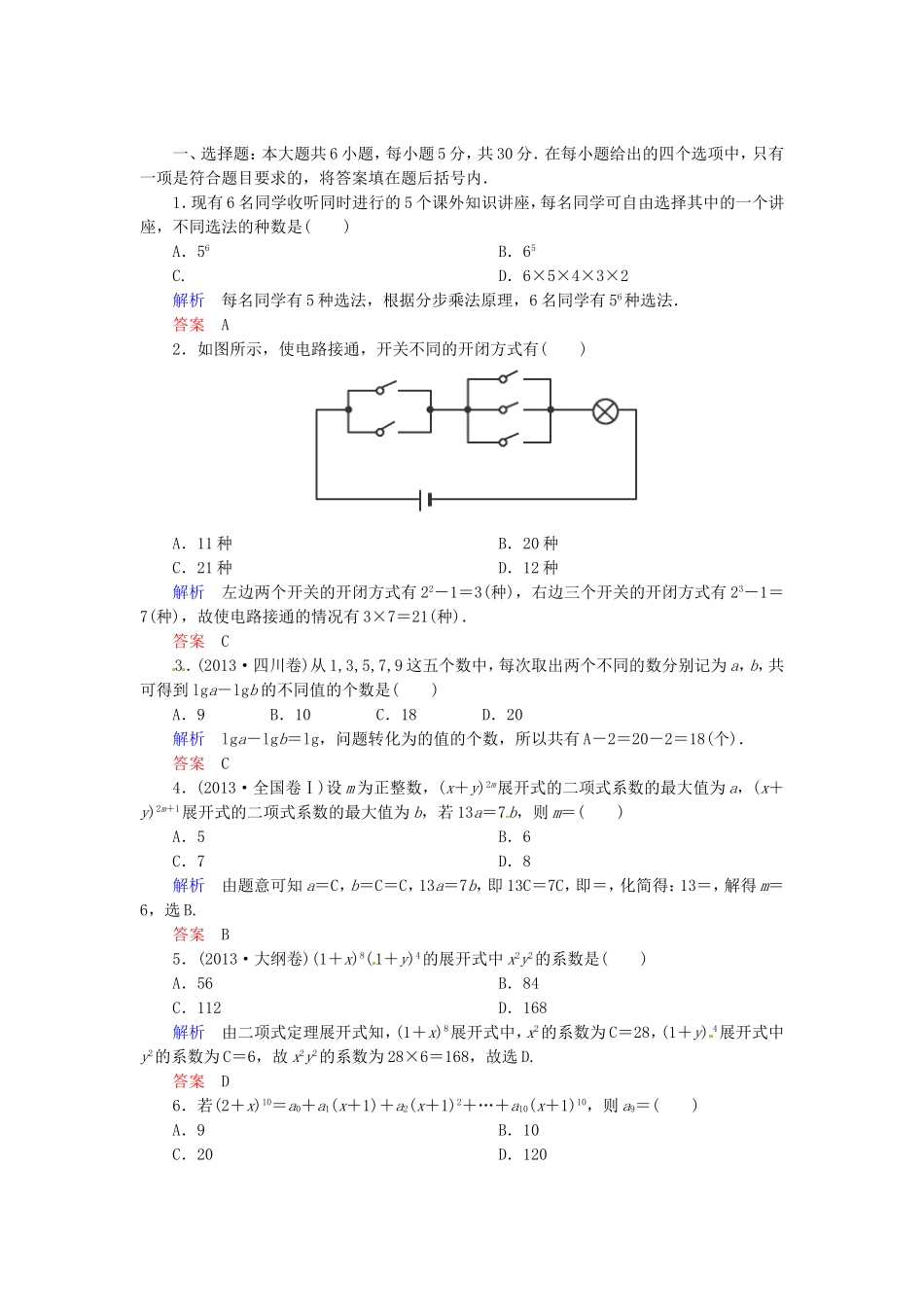
一、选择题:本大题共6小题,每小题5分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,将答案填在题后括号内.1.现有6名同学收听同时进行的5个课外知识讲座,每名同学可自由选择其中的一个讲座,不同选法的种数是()A.56B.65C.D.6×5×4×3×2解析每名同学有5种选法,根据分步乘法原理,6名同学有56种选法.答案A2.如图所示,使电路接通,开关不同的开闭方式有()A.11种B.20种C.21种D.12种解析左边两个开关的开闭方式有22-1=3(种),右边三个开关的开闭方式有23-1=7(种),故使电路接通的情况有3×7=21(种).答案C3.(2013·四川卷)从1,3,5,7,9这五个数中,每次取出两个不同的数分别记为a,b,共可得到lga-lgb的不同值的个数是()A.9B.10C.18D.20解析lga-lgb=lg,问题转化为的值的个数,所以共有A-2=20-2=18(个).答案C4.(2013·全国卷Ⅰ)设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m=()A.5B.6C.7D.8解析由题意可知a=C,b=C=C,13a=7b,即13C=7C,即=,化简得:13=,解得m=6,选B.答案B5.(2013·大纲卷)(1+x)8(1+y)4的展开式中x2y2的系数是()A.56B.84C.112D.168解析由二项式定理展开式知,(1+x)8展开式中,x2的系数为C=28,(1+y)4展开式中y2的系数为C=6,故x2y2的系数为28×6=168,故选D.答案D6.若(2+x)10=a0+a1(x+1)+a2(x+1)2+…+a10(x+1)10,则a9=()A.9B.10C.20D.120解析由题意a9=C=10,故选B.答案B二、填空题:本大题共3小题,每小题5分,共15分.将答案填在题中横线上.7.(2013·安徽卷)若8的展开式中x4的系数为7,则实数a=________.解析设第r+1项展开式为x4项,则展开式的通项可得Tr+1=Carx8-r;令8-r=4,可得r=3,故Ca3=7,易得a=.答案8.(2013·重庆卷)从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科、脑外科和内科医生都至少有1人的选派方法种数是________(用数字作答).解析骨科、脑外科和内科选派人数可能为(1,1,3),(2,2,1),(2,1,2),(1,2,2),(3,1,1),(1,3,1),故方法种数为CCC+CCC+CCC+CCC+CCC+CCC=590.答案5909.(2013·南京模拟)若对于任意实数x,有x5=a0+a1(x-2)+…+a5(x-2)5,则a1+a3+a5-a0=________.解析令x=3得a0+a1+…+a5=35,令x=1得a0-a1+…-a5=1,两式相减得a1+a3+a5==121,令x=2得a0=25=32,故a1+a3+a5-a0=121-32=89.答案89三、解答题:本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤.10.(本小题10分)若n展开式中前三项系数成等差数列.求:(1)展开式中含x的一次幂的项;(2)展开式中所有x的有理项.解由已知条件:C+C·=2C·,解得n=8(n=1,不合题意,舍去).(1)Tr+1=C()8-rr=C·2-r·x,令4-r=1,得r=4,∴x的一次幂的项为T4+1=C·2-4·x=x.(2)令4-r∈N(r≤8),则只有当r=0,4,8时,对应的项才是有理项,有理项分别为:T1=x4,T5=x,T9=.11.(本小题10分)已知(1+3x)n的展开式中,末三项的二项式系数的和等于121,求:(1)展开式中二项式系数最大的项;(2)展开式中系数最大的项.解(1)由已知得C+C+C=121,则n(n-1)+n+1=121,即n2+n-240=0,解得n=15,所以,展开式中二项式系数最大的项是T8=C(3x)7和T9=C(3x)8.(2)Tr+1=C(3x)r,由题意得,设第r+1项系数最大,则∴11≤r≤12.所以展开式中系数最大的项对应的r=11、12,即展开式中系数最大的项是T12=C(3x)11和T13=C(3x)12.12.(本小题10分)某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取4名工人进行技术考核.(1)求从甲、乙两组各抽取的人数;(2)求从甲组抽取的工人中恰有1名女工人的概率;(3)求抽取的4名工人中恰有2名男工人的概率.解(1)由于甲组和乙组各有10名工人,所以按分层抽样抽取样本4人,甲、乙两组各有2人被抽取.(2)设A表示事件:从甲组抽取的工人中恰有1名女工人,则P(A)==.(3)Ai表示事件:从甲组抽取的2名工人中恰有i名男工人,i=0,1,2.Bj表示事件:从乙组抽取的2名工人中恰有j名男工人,j=0,1,2.B表示事件:抽取的4名工人中恰有2名男工人.Ai与Bj独立,i,j=0,1,2,且B=A0·B2+A1·B1+A2·B0.故P(B)=P(A0·B2+A1·B1+A2·B0)=P(A0)·P(B2)+P(A1)·P(B1)+P(A2)·P(B0)=·+·+·=.