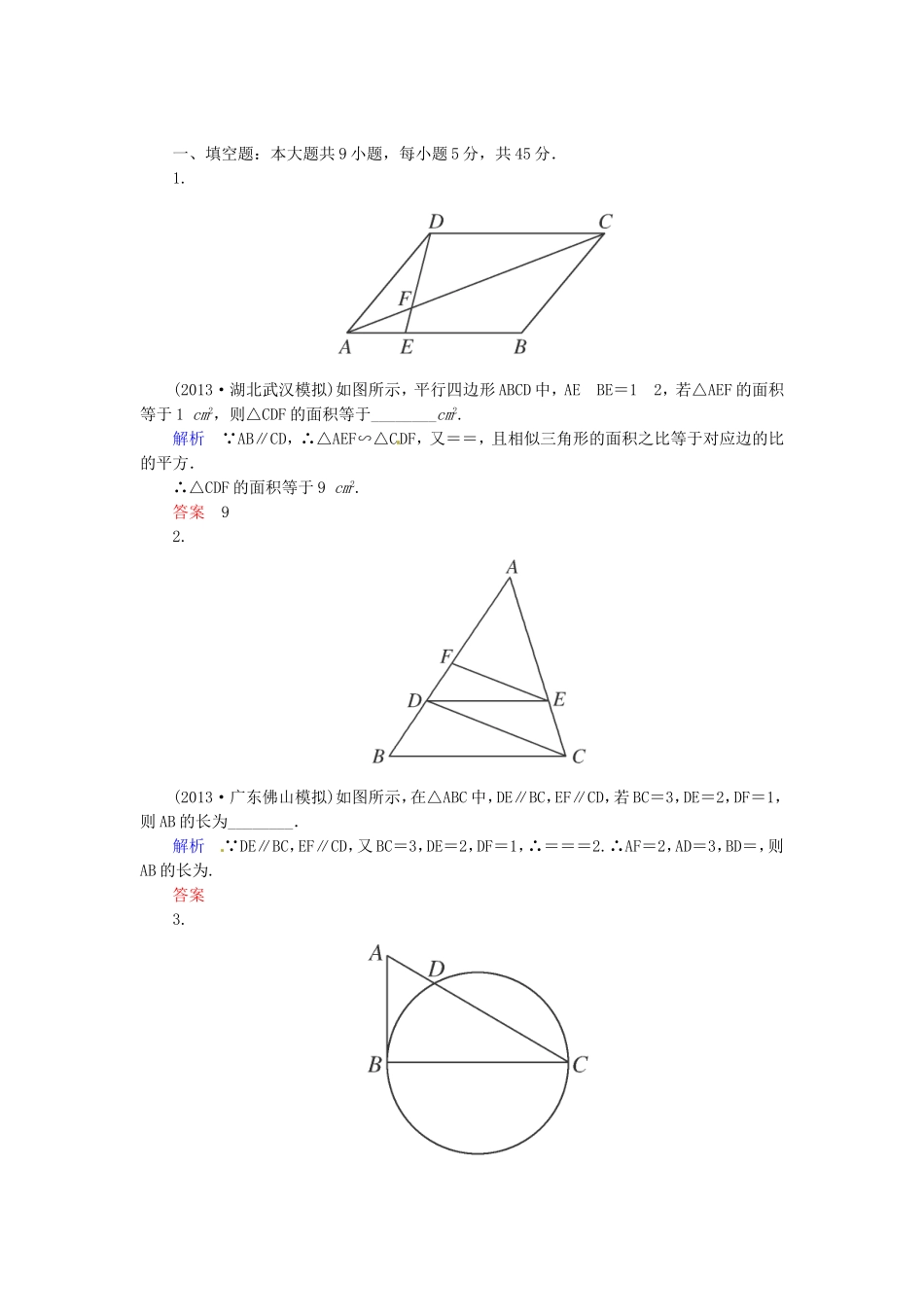
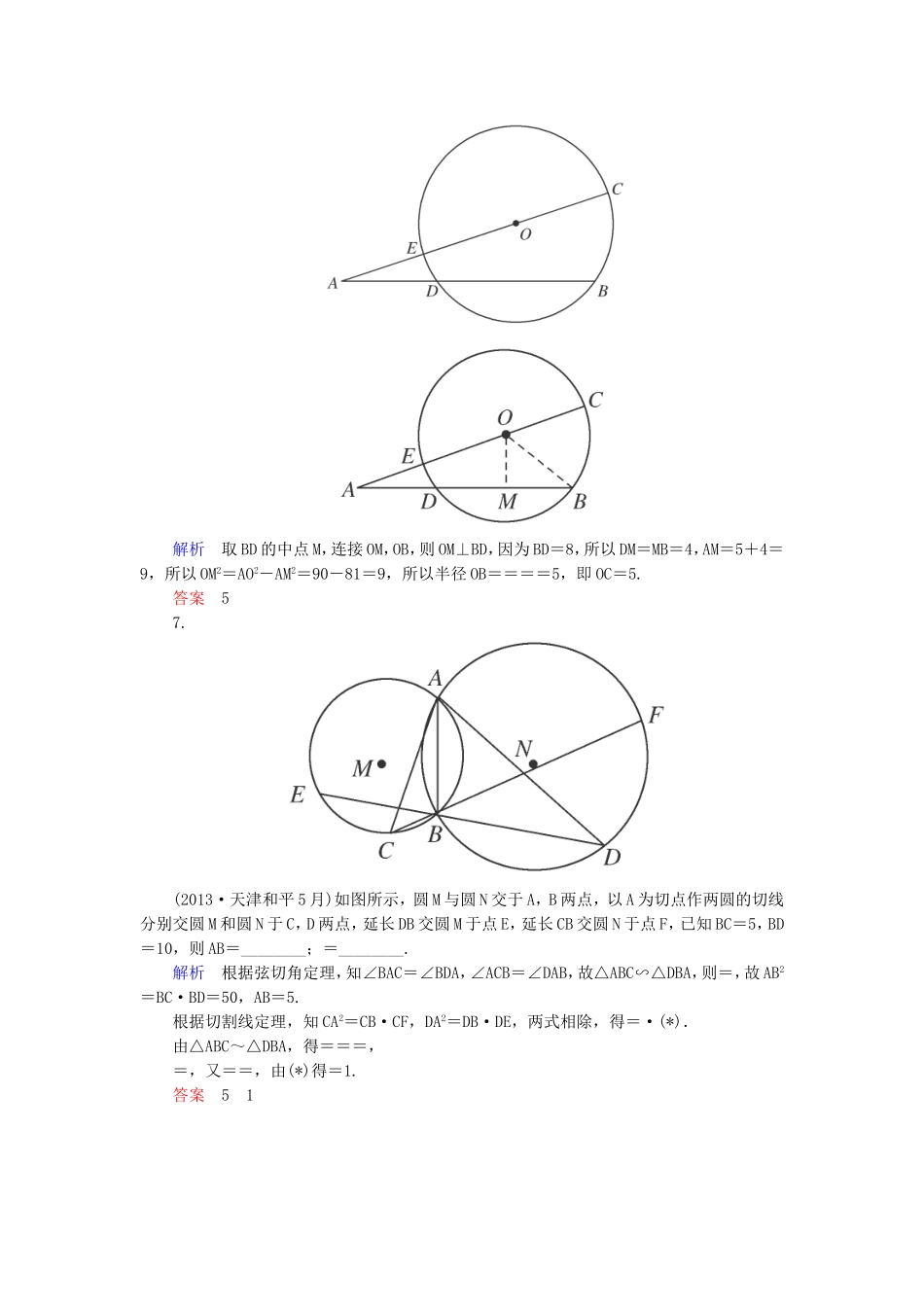
一、填空题:本大题共9小题,每小题5分,共45分.1.(2013·湖北武汉模拟)如图所示,平行四边形ABCD中,AEBE=12,若△AEF的面积等于1cm2,则△CDF的面积等于________cm2.解析 AB∥CD,∴△AEF∽△CDF,又==,且相似三角形的面积之比等于对应边的比的平方.∴△CDF的面积等于9cm2.答案92.(2013·广东佛山模拟)如图所示,在△ABC中,DE∥BC,EF∥CD,若BC=3,DE=2,DF=1,则AB的长为________.解析 DE∥BC,EF∥CD,又BC=3,DE=2,DF=1,∴===2.∴AF=2,AD=3,BD=,则AB的长为.答案3.如图所示,直角三角形ABC中,∠B=90°,AB=4,以BC为直径的圆交边AC于点D,AD=2,则∠C的大小为________.解析连接BD, BC为直径,∴∠BDC=90°.∴∠ABD=∠BCD,在直角△ABD中, AD=2,AB=4,∴∠ABD=30°,故∠C=∠ABD=30°.答案30°4.(2013·重庆卷)如图所示,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为________.解析由已知BC=ABsin60°=10,由弦切角定理∠BCD=∠A=60°,所以BD=BCsin60°=15,CD=BCcos60°=5,由切割线定理CD2=DE·BD,所以DE=5.答案55.(2013·湖北卷)如图所示,圆O上一点C在直径AB上的射影为D,点D在半径OC上的射影为E.若AB=3AD,则的值为________.解析连接AC,BC,则AC⊥BC,又AB=3AD,则AD=AB,BD=AB,OD=AB,OC=AB,△ABC中,CD2=AD·BD=AB2,△OCD中,OD2=OE·OC,CD2=CE·OC可得:OE=AB,CE=AB,=8.答案86.(2013·广东惠州5月)如图所示,已知AD=5,BD=8,AO=3,则圆O的半径OC的长为________.解析取BD的中点M,连接OM,OB,则OM⊥BD,因为BD=8,所以DM=MB=4,AM=5+4=9,所以OM2=AO2-AM2=90-81=9,所以半径OB====5,即OC=5.答案57.(2013·天津和平5月)如图所示,圆M与圆N交于A,B两点,以A为切点作两圆的切线分别交圆M和圆N于C,D两点,延长DB交圆M于点E,延长CB交圆N于点F,已知BC=5,BD=10,则AB=________;=________.解析根据弦切角定理,知∠BAC=∠BDA,∠ACB=∠DAB,故△ABC∽△DBA,则=,故AB2=BC·BD=50,AB=5.根据切割线定理,知CA2=CB·CF,DA2=DB·DE,两式相除,得=·(*).由△ABC~△DBA,得===,=,又==,由(*)得=1.答案518.(2013·陕西卷)如图所示,弦AB与CD相交于⊙O内一点E,过E作BC的平行线与AD的延长线交于点P,已知PD=2DA=2,则PE=________.解析由PE∥BC得∠PED=∠C=∠A,△APE中与△EPD中,∠APE=∠EPD,∠PED=∠A,故△PDE∽△PEA,则=,即PE2=PA·PD,又PA=PD+DA=3;PD=2,故PE2=2×3=6,则PE=.答案9.(2013·天津卷)如图所示,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5,则线段CF的长为________.解析由切割线定理EA2=EB·ED,得62=EB·(EB+5),经计算EB=4,∠EAB=∠ACB=∠ABC,所以AE∥BC,又因为AC∥BD,所以四边形AEBC是平行四边形,可得BC=AE=6,AC=EB=4.∠C=∠C,∠CAF=∠D=∠C=∠ABC,所以△CAF∽△CBA,所以=,即CF===.答案二、解答题:本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤.10.(本小题10分)(2013·云南大理二模)如图所示,在正△ABC中,点D,E分别在边BC,AC上,且BD=BC,CE=CA,AD,BE相交于点P,求证:(1)四点P、D、C、E共圆;(2)AP⊥CP.证明(1)在△ABC中,由BD=BC,CE=CA知△ABD≌△BCE,∴∠ADB=∠BEC,即∠ADC+∠BEC=π.∴四点P、D、C、E共圆.(2)如图所示,连接DE.在△CDE中,CD=2CE,∠ACD=60°,由正弦定理知∠CED=90°.由四点P,D,C,E共圆知,∠DPC=∠DEC,所以AP⊥CP.11.(本小题10分)(2013·全国卷Ⅱ)如图所示,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B、E、F、C四点共圆.(1)证明:CA是△ABC外接圆的直径;(2)若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值.思路分析本题考查圆的基本性质、三角形相似定理...