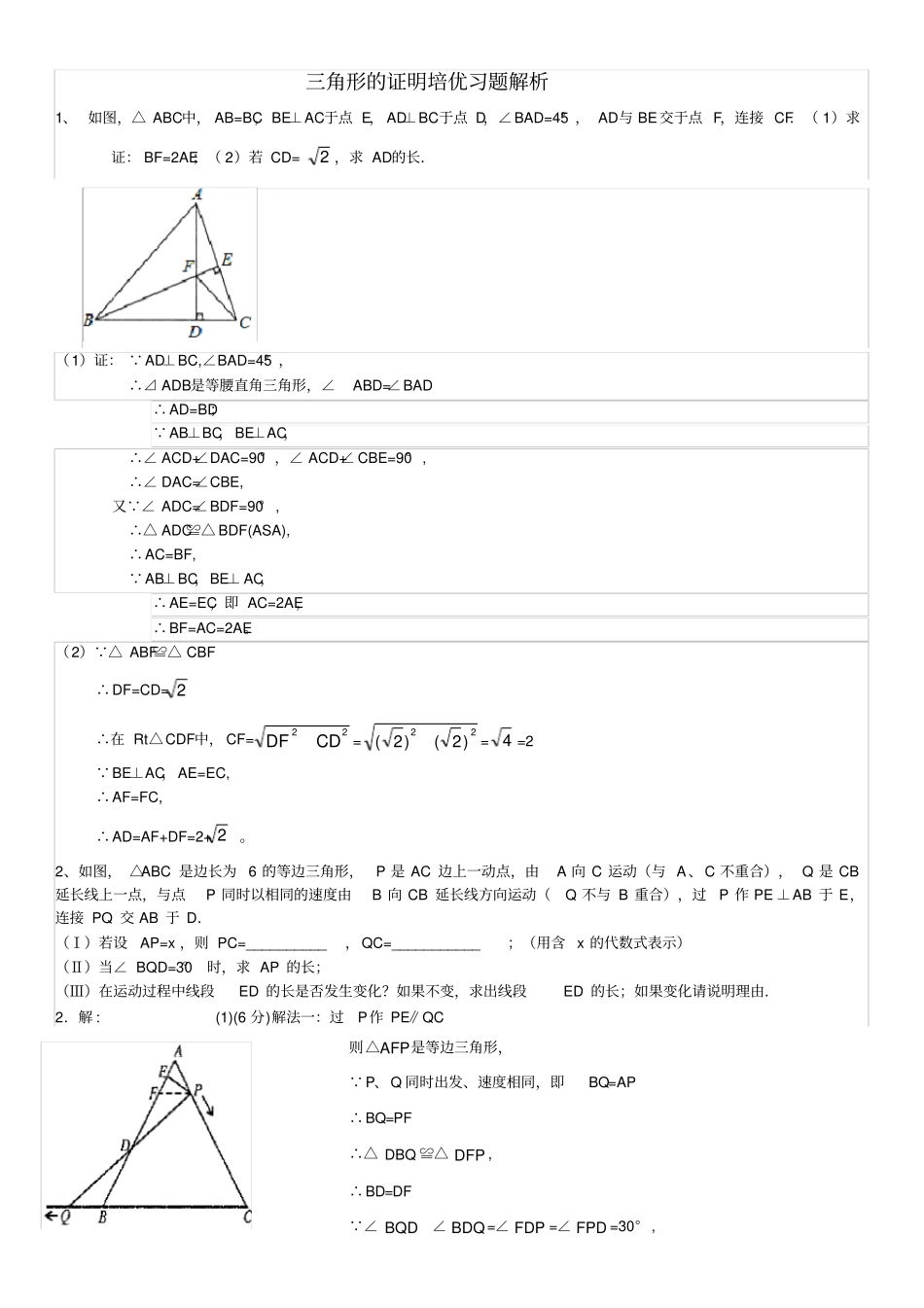
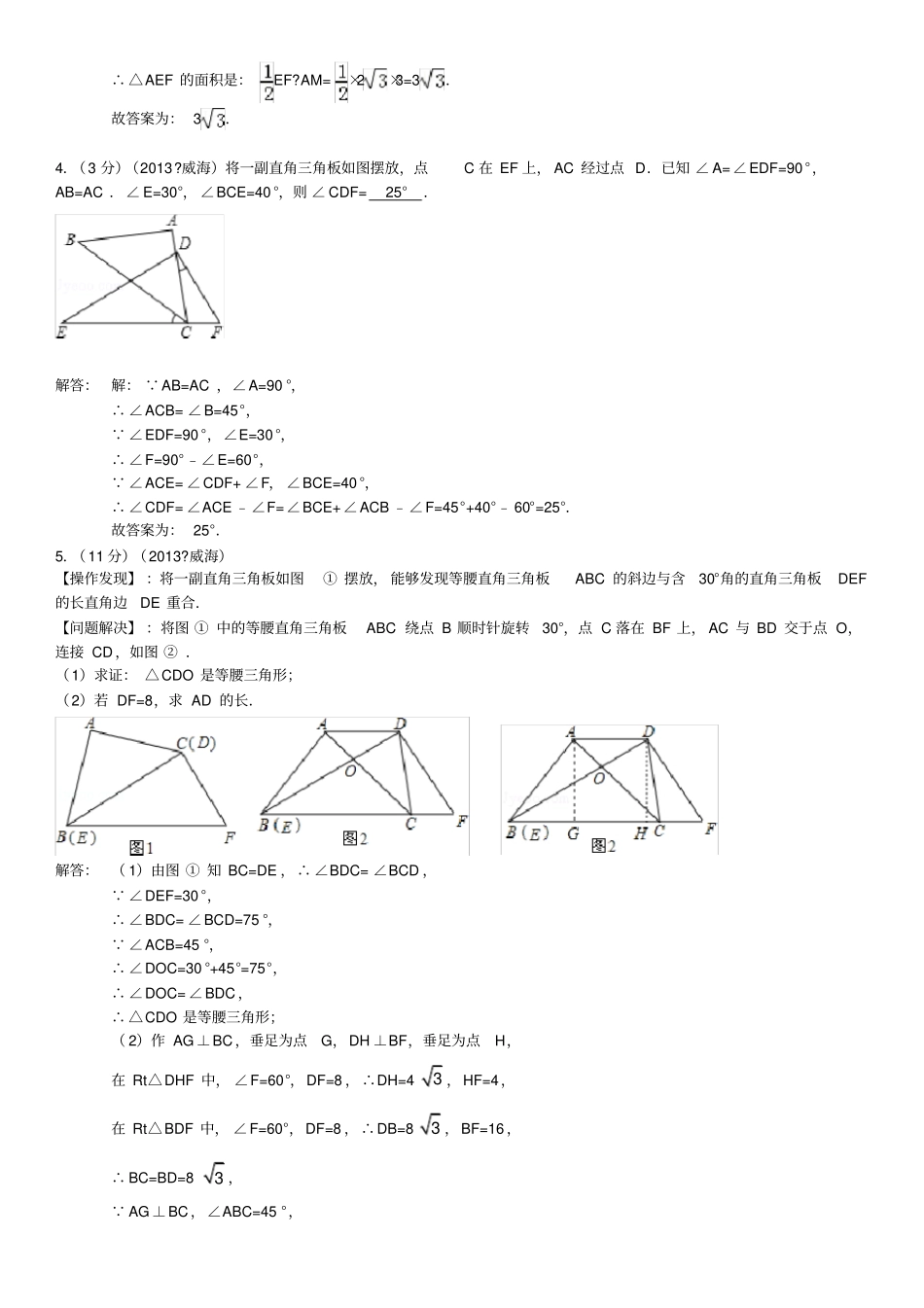
三角形的证明培优习题解析1、如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.(1)求证:BF=2AE;(2)若CD=2,求AD的长.(1)证: AD⊥BC,∠BAD=45°,∴⊿ADB是等腰直角三角形,∠ABD=∠BAD∴AD=BD; AB⊥BC,BE⊥AC,∴∠ACD+∠DAC=90°,∠ACD+∠CBE=90°,∴∠DAC=∠CBE,又 ∠ADC=∠BDF=90°,∴△ADC≌△BDF(ASA),∴AC=BF, AB⊥BC,BE⊥AC,∴AE=EC,即AC=2AE,∴BF=AC=2AE。(2) △ABF≌△CBF∴DF=CD=2∴在Rt△CDF中,CF=22CDDF=22)2()2(=4=2 BE⊥AC,AE=EC,∴AF=FC,∴AD=AF+DF=2+2。2、如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.(Ⅰ)若设AP=x,则PC=__________,QC=___________;(用含x的代数式表示)(Ⅱ)当∠BQD=30°时,求AP的长;(Ⅲ)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.2.解:(1)(6分)解法一:过P作PE∥QC则△AFP是等边三角形, P、Q同时出发、速度相同,即BQ=AP∴BQ=PF∴△DBQ≌△DFP,∴BD=DF ∠BQD∠BDQ=∠FDP=∠FPD=30°,∴BD=DF=FA=31AB=631=2,∴AP=2.解法二: P、Q同时同速出发,∴AQ=BQ设AP=BQ=x,则PC=6-x,QC=6+x在Rt△QCP中,∠CQP=30°,∠C=60°∴∠CQP=90°∴QC=2PC,即6+x=2(6-x)∴x=2∴AP=2(2)由(1)知BD=DF而△APF是等边三角形,PE⊥AF, AE=EF又DE+(BD+AE)=AB=6,∴DE+(DF+EF)=6,即DE+DE=6 DE=3为定值,即DE的长不变3.(3分)(2013?临沂)如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是3.解答:解: 四边形ABCD是菱形,∴BC=CD,∠B=∠D=60°, AE⊥BC,AF⊥CD∴AB?AE=CD?AF,∠BAE=∠DAF=30°,∴AE=AF, ∠B=60°,∴∠BAD=120°,∴∠EAF=120°﹣30°﹣30°=60°,∴△AEF是等边三角形,∴AE=EF,∠AEF=60°, AB=4,∴AE=2,∴EF=AE=2,过A作AM⊥EF,∴AM=AE?cos60°=3,∴△AEF的面积是:EF?AM=×2×3=3.故答案为:3.4.(3分)(2013?威海)将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=25°.解答:解: AB=AC,∠A=90°,∴∠ACB=∠B=45°, ∠EDF=90°,∠E=30°,∴∠F=90°﹣∠E=60°, ∠ACE=∠CDF+∠F,∠BCE=40°,∴∠CDF=∠ACE﹣∠F=∠BCE+∠ACB﹣∠F=45°+40°﹣60°=25°.故答案为:25°.5.(11分)(2013?威海)【操作发现】:将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合.【问题解决】:将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,AC与BD交于点O,连接CD,如图②.(1)求证:△CDO是等腰三角形;(2)若DF=8,求AD的长.解答:(1)由图①知BC=DE,∴∠BDC=∠BCD, ∠DEF=30°,∴∠BDC=∠BCD=75°, ∠ACB=45°,∴∠DOC=30°+45°=75°,∴∠DOC=∠BDC,∴△CDO是等腰三角形;(2)作AG⊥BC,垂足为点G,DH⊥BF,垂足为点H,在Rt△DHF中,∠F=60°,DF=8,∴DH=43,HF=4,在Rt△BDF中,∠F=60°,DF=8,∴DB=83,BF=16,∴BC=BD=83, AG⊥BC,∠ABC=45°,∴BG=AG=43,∴AG=DH, AG∥DH,∴四边形AGHD为矩形,∴AD=GH=BF﹣BG﹣HF=16﹣43﹣4=12﹣43.6.(本题满分10分)如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.⑴求证:△BAD≌△AEC;⑵若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.解析:(1)证明: AB=AC,∴∠B=∠ACB.又 四边形ABDE是平行四边形∴AE∥BD,AE=BD,∴∠ACB=∠CAE=∠B,∴⊿DBA≌⊿AEC(SAS)⋯⋯⋯⋯⋯⋯4分(2)过A作AG⊥BC,垂足为G.设AG=x,在Rt△AGD中, ∠ADC=450,∴AG=DG=x,在Rt△AGB中, ∠B=300,∴BG=x3,⋯⋯⋯⋯⋯⋯6分又 BD=10.∴BG-DG=BD,即103xx,解得AG=x=5351310.⋯⋯⋯⋯⋯⋯⋯8分∴S平行四边形ABDE=BD·AG=10×(535)=50350.⋯⋯⋯⋯⋯⋯10...