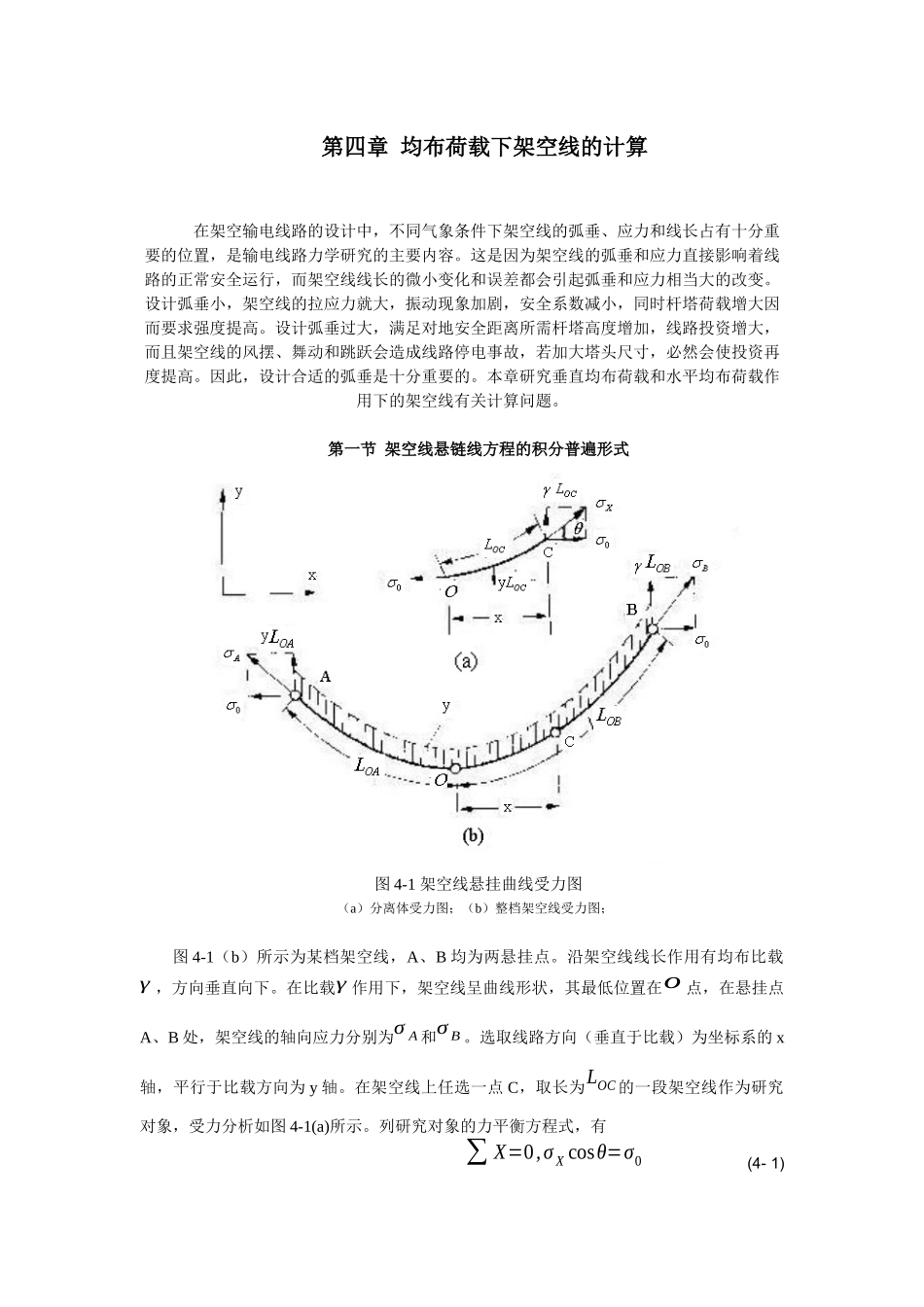
第四章均布荷载下架空线的计算在架空输电线路的设计中,不同气象条件下架空线的弧垂、应力和线长占有十分重要的位置,是输电线路力学研究的主要内容。这是因为架空线的弧垂和应力直接影响着线路的正常安全运行,而架空线线长的微小变化和误差都会引起弧垂和应力相当大的改变。设计弧垂小,架空线的拉应力就大,振动现象加剧,安全系数减小,同时杆塔荷载增大因而要求强度提高。设计弧垂过大,满足对地安全距离所需杆塔高度增加,线路投资增大,而且架空线的风摆、舞动和跳跃会造成线路停电事故,若加大塔头尺寸,必然会使投资再度提高。因此,设计合适的弧垂是十分重要的。本章研究垂直均布荷载和水平均布荷载作用下的架空线有关计算问题。第一节架空线悬链线方程的积分普遍形式图4-1架空线悬挂曲线受力图(a)分离体受力图;(b)整档架空线受力图;图4-1(b)所示为某档架空线,A、B均为两悬挂点。沿架空线线长作用有均布比载γ,方向垂直向下。在比载γ作用下,架空线呈曲线形状,其最低位置在ο点,在悬挂点A、B处,架空线的轴向应力分别为σA和σB。选取线路方向(垂直于比载)为坐标系的x轴,平行于比载方向为y轴。在架空线上任选一点C,取长为LOC的一段架空线作为研究对象,受力分析如图4-1(a)所示。列研究对象的力平衡方程式,有∑X=0,σXcosθ=σ0(4-1)∑Y=0,σXsinθ=γLOC(4-2)式(4-1)表明,架空线上任一点C处的轴向应力σX的水平分量等于弧垂最低点处的轴向应力σ0,即架空线上轴向应力的水平分量处处相等,式(4-2)表明,架空线上任一点轴向应力的垂向分量等于该点到弧垂最低点间线长LOC与比载γ之积。以上两式相除可得tgθ=γσ0LOCdydx=γσ0LOC(4-3)上式为悬链线方程的徽分形式。从中可以看出,当比值γ/σ0一定时,架空线上任一点处的斜率与该点至弧垂最低点之间的线长成正比。在弧垂最低点O处,曲线的斜率为零,即θ=0,将式(4-3)写成y'=γσ0LOC两边微份dy'=γσ0d(L0C)=γσ0√(dx)2+(dy)2=γσ0√1±y¿dx分离变量后两端积分∫dy'√1+y¿=γσ0∫dxarcsh(y')=γσ0(x+C1)或写成dydx=shγσ0(x+C1)(4-4)上式两端积分,得y=σ0γchγσ0(x+C1)+C2(4-5)式(4-5)是架空线悬链线方程的积分普遍形式。其中C1、C2为积分常数,其值取决于坐标系的原点位置。第二节等高悬点架空线的弧垂、线长和应力一、等高悬点架空线的悬链线方程等高悬点是指架空线的两个悬挂点高度相同。由于对称性,等高悬点架空线的弧垂最低点位于档距中央,将坐标原为取在该点,如图4-2所示。图4-2等高悬点架空线的悬链线当x=0时,dydx=0,代入式(4-4)可解得C1=0;当x=0时,y=0,代入式(4-5)并利用C1=0,解得C1=−σ0γ,将C1、C2的值代回式(4-5),并加以整理即可得到架空线的悬链线方程y=σ0γ(chγσ0x−1)(4-6)由式(4-6)可以看出,架空线的悬链线具体形状完全由比值σ0/γ决定,即无论是何种架空线,何种气象条件,只要σ0/γ相同,架空线的悬挂曲线形状就相同。在比载γ一定的情况下,架空线的水平应力σ0是决定悬链线形状的唯一因素,所以架线时的水平张力对架空线的空间形状有着决定性的影响。在导出式(4-6)的过程中,并没有用到等高悬点的限定条件,因此式(4-6)同样可用于不等高悬点的情况。二、等高悬点架空线的弧垂架空线上任一点的弧垂是指该点距两悬挂点连线的垂向距离。在架空输电线路设计中,需计算架空线任一点x处的弧垂fX,以验算架空线对地安全距离,参见图4-2,显然fX=yB−y而yB=σ0γ(chrl2σ0−1)所以fX=σ0γ[chγl2σ0−chγxσ0]=σ0γ[chγl2σ0−chr(l−2x1)2σ0](4-7)利用恒等式chα-chβ=2shα+β2shα−β2对上式进行变换,可以得到fX=2σ0γshrx12σ0shr(l−x1)2σ0(4-8)在档距中央,弧垂有最大值f,此时x=0或x1=l2,所以有f=yB=σ0γ(chγl2σ0−1]=2σ0γsh2γl4σ0(4-9)除非特别说明,架空线的弧垂一般指的是最大弧垂。最大弧垂在线路的设计、施工中占有十分重要的位置。三、等高悬点架空线的线长弧垂最低点O与任一点C之间的架空线长度LOC(参见图4-1)可由式(4-3)和式(4-4)联立求解,并考虑到C1=0而得到。线长LOC计算式为LOC=σ0γshrxσ0或记为LX=σ0...