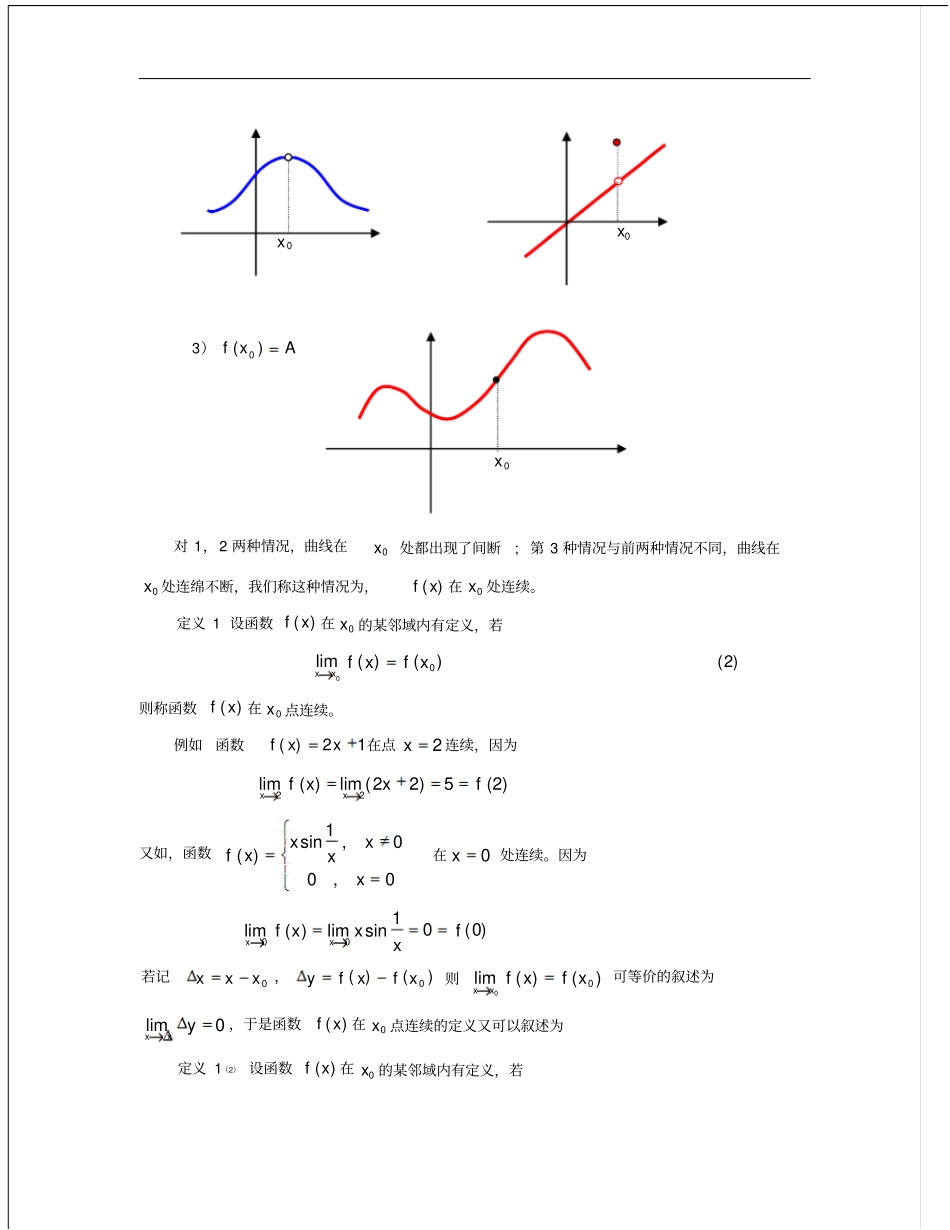
第四章函数的连续性§1连续性的概念(一)教学目的:掌握函数连续性概念.(二)教学内容:深刻理解函数连续,函数左右连续,区间上函数连续,间断点及其分类等概念.对一般的函数特别是初等函数可以讨论其间断点并且分类.基本要求:1)掌握函数连续性概念,可去间断点,跳跃间断点,第二类间断点,区间上的连续函数的定义.2)较高要求:讨论黎曼函数的连续性.(三)教学建议:(1)函数连续性概念是本节的重点.对学生要求懂得函数在一点和在区间上连续的定义,间断点的分类.(2)本节的难点是用较高的分析方法、技巧证明函数的连续性,对较好学生布置有关习题.————————————————————————————一函数在一点0x的连续先回顾一下函数在0x点的极限Axfxx)(lim0设函数)(xf在0x的某个空心邻域内有定义,A是一个确定的数,若对0,0,当||00xx时,都有|)(|Axf,则称)(xf在0xx时,以A为极限。这里)(0xf可以有三种情况1))(0xf无定义,比如上章讲过的特殊极限1)sin(lim000xxxxxx2)Axf)(0,比如00,1,)(xxxxxxxf,)()(lim000xfxxfxx3)Axf)(0对1,2两种情况,曲线在0x处都出现了间断;第3种情况与前两种情况不同,曲线在0x处连绵不断,我们称这种情况为,)(xf在0x处连续。定义1设函数)(xf在0x的某邻域内有定义,若)()(lim00xfxfxx)2(则称函数)(xf在0x点连续。例如函数12)(xxf在点2x连续,因为)2(5)22(lim)(lim22fxxfxx又如,函数0,00,1sin)(xxxxxf在0x处连续。因为)0(01sinlim)(lim00fxxxfxx若记)()(,00xfxfyxxx则)()(lim00xfxfxx可等价的叙述为0limyxx,于是函数)(xf在0x点连续的定义又可以叙述为定义1(2)设函数)(xf在0x的某邻域内有定义,若0x0x0x0lim0yx则称)(xf在0x点连续。另外,由于函数)(xf在0x点连续是用极限形式表述的,若将)()(lim00xfxfxx改用语言叙述,则)(xf在0x点连续又可以定义为:定义1(3)设函数)(xf在0x的某邻域内有定义,若对0,0,使得当||0xx时,都有|)()(|0xfxf,)2(则称)(xf在0x点连续。注意函数)(xf在0x点连续,不仅要求)(xf在0x点有定义,而且要求0xx时,)(xf的极限等于)(0xf,因此这里在极限的“”语言叙述中把“||00xx”换成了“||0xx”。最后,)1(式又可表示为)lim()(lim00xfxfxxxx,可见“f在0x连续”意味着极限运算0limxx对应法则f的可交换性。例1证明函数)()(xxDxf在点0x连续,其中)(xD为狄利克雷函数。证明由0)0(f及1)(xD,对于任意的0,为使xxxDfxf)()0()(只要取,即可按定义推得在连续。相应于在的左、右极限的概念,我们给出左右连续的定一如下:定义2设函数)(xf在0x的某左(右)邻域内有定义,若)()(lim00xfxfxx()()(lim00xfxfxx)则称)(xf在0x点左(右)连续。由极限与单侧极限的关系不难得出:定理4.1函数)(xf在0x点连续的充分必要条件为:)(xf在0x点既左连续又右连续。例2讨论函数0,20,2)(xxxxxf在0x的连续性。解因为)0(2)2(lim)(lim)0(2)2(lim)(lim0000fxxffxxfxxxx所以)(xf在0x右连续,但不左连续,从而)(xf在0x不连续。二间断点及其分类定义3设函数f在某)(0xUo内有定义。若f在点0x无定义,或在点0x有定义但不连续,则称点0x为函数f的间断点或不连续点。由连续的定义知,函数)(xf在0x点不连续必出现如下情形:1)Axfxx)(lim0,而f在点0x无定义,或有定义但)()(lim00xfAxfxx2)左、右极限都存在,但不相等,称|)(lim)(lim|00xfxfxxxx为跳跃度3)左、右极限至少一个不存在据此,函数f的间断点可作如下分类:1.可去间断点情况1)0x称为可去间断点(或可去不连续点);例0,10,sin)(xxxxxf,)0(11)(lim0fxfx0x是)(xf的可去间断点。2-20例0)(,1)(lim,|)sgn(|)(afxfaxxfax,ax是)(xf的可去间断点。2.跳跃间断点情况2)0x称为可跳跃间断点;情况1),2)统称第一类间断点。例][xy因为1lim,)(lim0nnxfxxnx,所以][xy的整数点为跳跃间断点,跳跃度等1.例xxfsgn)(因为1sgnlim,1sgnlim00xxxx所以xxfsgn)(在0x处为跳跃间断点,跳跃度等2.3.情况3)0x称为可第二类间断点;例)(lim,1)(0xfxxfx不存在,所以0x是)(xf的第二类不连续点。为了加强理解和记忆,我们画出两类不连续点的图象(c41)subplot(2,2,1)ezplot('sin(x)/x',[-0.5,0.5])holdonplot(...