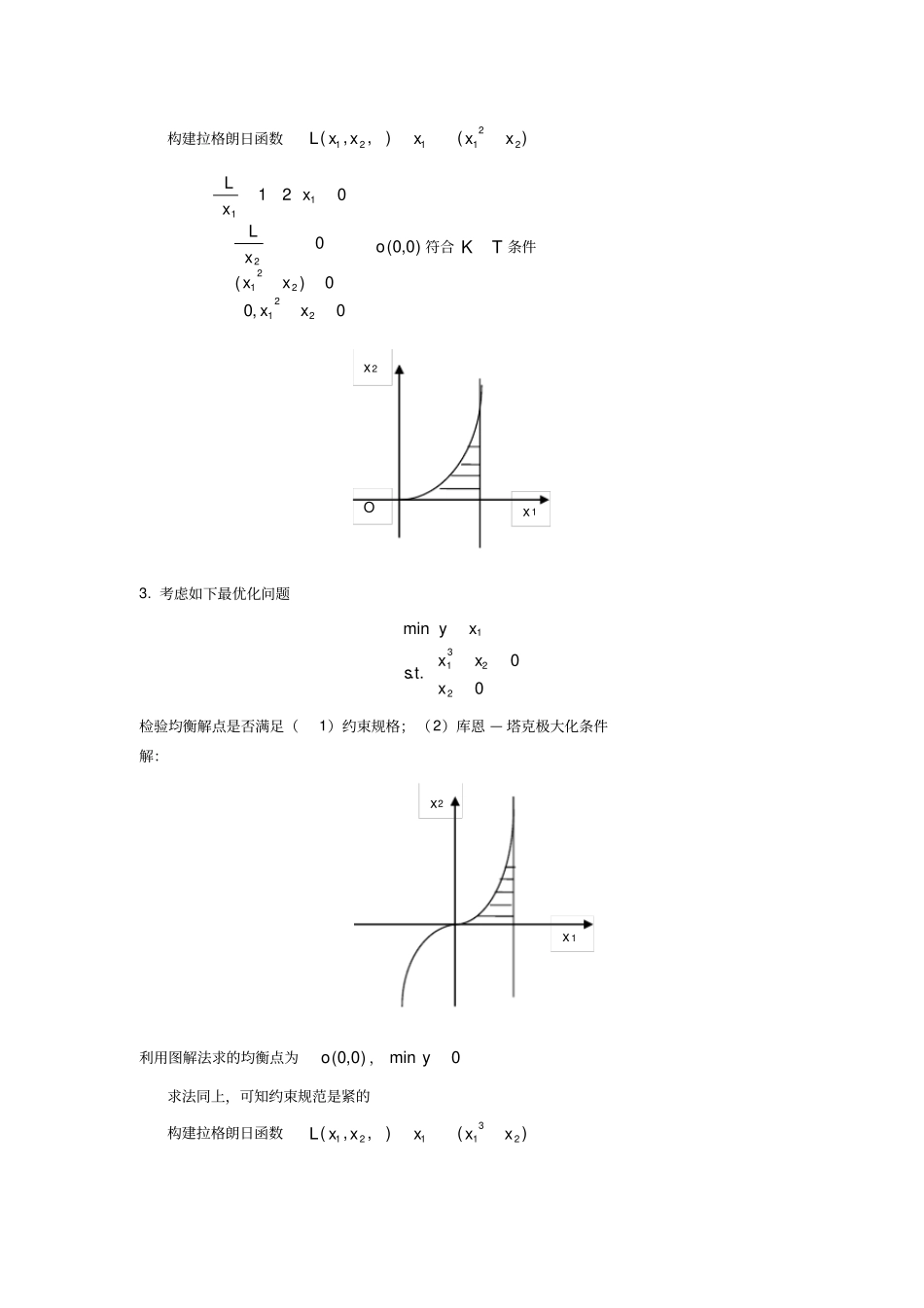
第六章习题答案1.考虑如下最优化问题0,1..max2121211xxxxtsxy用图解法解此题。并检验均衡解点是否满足(1)约束规格;(2)库恩—塔克极大化条件解:可行域为OAB利用图解法求的均衡点为)0,1(B,1maxy对于)0,1(B来说,有112221xx,因此该约束规格是紧的。构建拉格朗日函数)1(),,(2221121xxxxxL01,00)1(020212221222122211xxxxxxLxxxL)0,1(B符合TK条件2.考虑如下最优化问题0,0..min212211xxxxtsxy用图解法解此题。并检验均衡解点是否满足(1)约束规格;(2)库恩—塔克极大化条件解:利用图解法求的均衡点为)0,0(o,0miny求法同上,可知约束规范是紧的BAOx1x2构建拉格朗日函数)(),,(221121xxxxxL0,00)(0021221221211xxxxxLxxL)0,0(o符合TK条件3.考虑如下最优化问题00..min22311xxxtsxy检验均衡解点是否满足(1)约束规格;(2)库恩—塔克极大化条件解:利用图解法求的均衡点为)0,0(o,0miny求法同上,可知约束规范是紧的构建拉格朗日函数)(),,(231121xxxxxLx1Ox2x2x10,00)(00312312312211xxxxxLxxL)0,0(o不符合TK条件4.写出下面优化问题的一阶必要条件0,,2..),,(max222zyxzyxtszyxzyxf解:)2(),,(22221zyxzyxxxL一阶必要条件为:0)2(,0021021021222zyxzzLyyLxxL5.求解下面最优化问题(1)0,122..4max22yxyxtsyxx(2)0,160..min212212121xxxxxxxtsxxy(3)0,,302105..10540min3213121321xxxxxxxtsxxxy(4)0,04..),(max21222122121xxxxtsxxxxf(5)0,16..max212121xxxxtsxxy解:(1)22(,,)4(221)Lxyxxyxy一阶必要条件为:2120820(221)00,221LxxLyyxyxy解得314,,1055xy(2)图解法可行域为314,,1055xy,均衡解点(1,1)min2Ay(3)12312123112213(,,,,)40510(105)(302)Lxxxxxxxxxx一阶必要条件为:x1BCA0x212112231122131212134052050100(105)0(3023)0,0,510230LxLxLxxxxxxxxx(4)222121212(,,)(4)Lxxxxxx一阶必要条件为:1122222122212120220(4)00,4LxxLxxxxxxx解得1212,0,4xx(5)121212(,,)(16)Lxxxxxx一阶必要条件为:2112121200(16)00,16LxxLxxxxxx解得128xx6.考虑如下最优化模型0,0)1(..max213121xxxxtsxy证明:(1)均衡解12,1,0xx不满足库恩-塔克条件;(2)当引进新乘数00,把拉格朗日函数修改成如下形式niimiinxxxgrxxxfZ,,,,,,2112100,则在点0,1处满足库恩-塔克条件。解:(1)312112(,,)(1)Lxxxxx一阶必要条件为:211231231213(1)00(1)00,(1)0LxxLxxxxx不符合K-T条件。(2)此时,31200112(,,,)(1)Lxxxxx一阶必要条件为:201123123123(1)00(1)00,(1)0LxxLxxxxx当00时,符合K-T条件7.消费者对两种商品的偏好用效用函数表示为2121),(xxxxU假设消费者的收入为12元,两种商品价格分别为2,121pp。试求最优的商品组合。解:由题意知,112212212PxPxxx121212(,,)(212)Lxxxxxx一阶必要条件为:2111221212020(212)00,212LxxxLxxxxxxx解得1226,3,2xx8.求解消费者问题MxpxptsxxxU221121..ln)(max效用极大值点,并利用二阶充分条件判断极大值点是否为最大化值点。解:12121122(,,)ln()LxxxxpxpxM一阶必要条件为:1122211221122100()00,LpxLpxxpxpxMpxpxM解得1121211,,Mpxxppp1222120000pHpxpp验证其为负定。9.一个消费者生活在小岛上,那里只生产两种产品,x和y,生产可能前沿是20022yx,他消费所有的产品,她的效用函数是3xyU,这个消费者同时面临环境对于她所能生产的两种产品总额上的约束,约束条件是20xy(1)写出库恩—塔克一阶条件(2)求消费者最优的x和y,确定约束条件是否发挥限制作用。解:(1)32211212(,,,)(200)(20)LxyxyxyxyK-T一阶条件为:31221222212221220320(200)0(20)0,0,2000200LyxxLxyyxxyxyxyxy(2)假设第二个约束条件(定量配额)没有发挥作用,由互补松弛性得20,故有312122120320(200)0yxxyyxy解得152,56,753xy,因20xy故为K-T条件最终解。反之2132222030(20)0yxyxy解得25,15,3375xy,因22200xy故被拒绝。10.一家电子公司在外国设立一个发电站。现在需要规划其产能。电力需求的高峰时段的需求函数是11400QP,非高峰时段的需求函数是22380QP。变动成本是20(两个市场都要支付),产能成本是每单位10,只要一次支付并且可以在两个时期中使用。(1)写出...