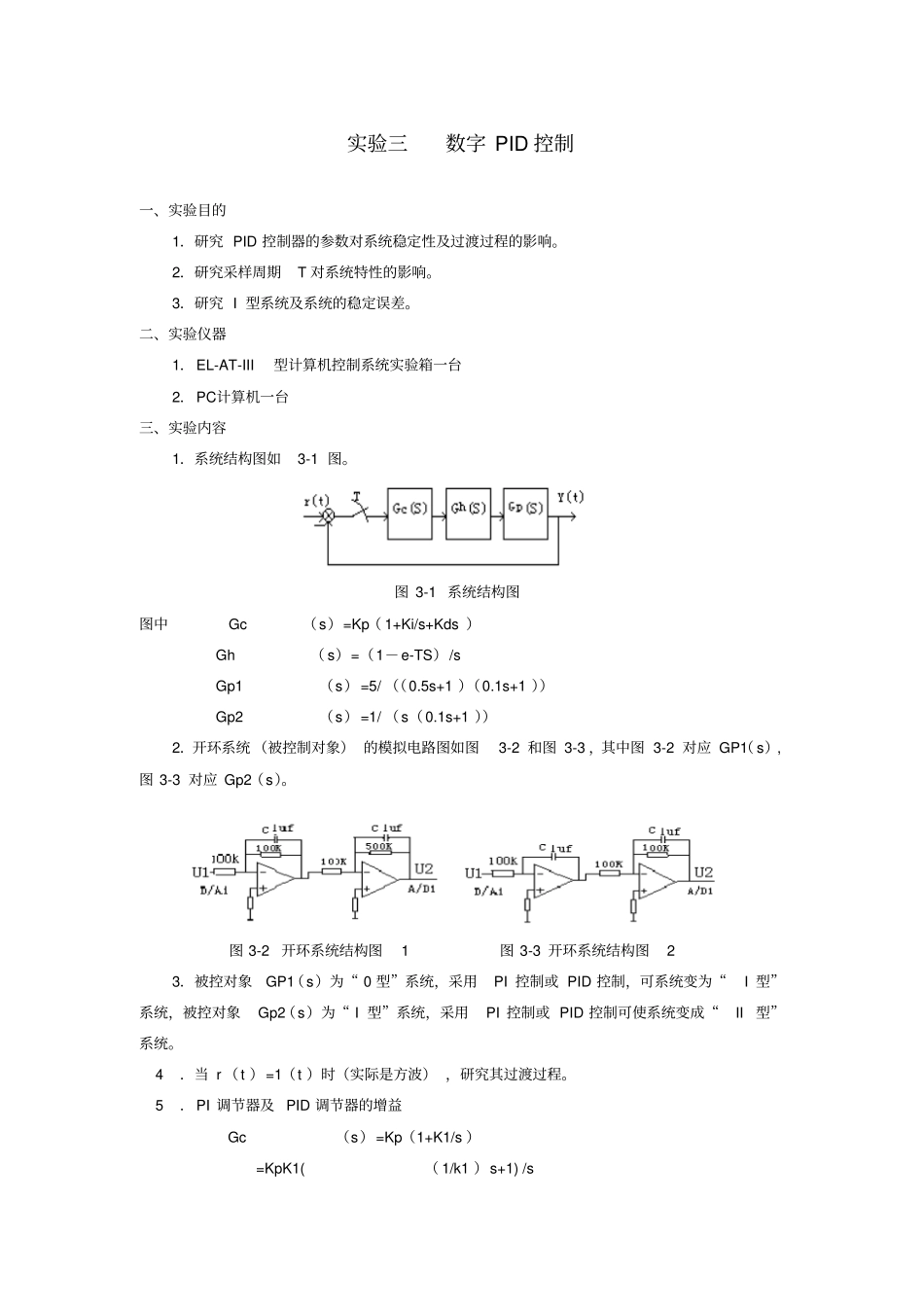
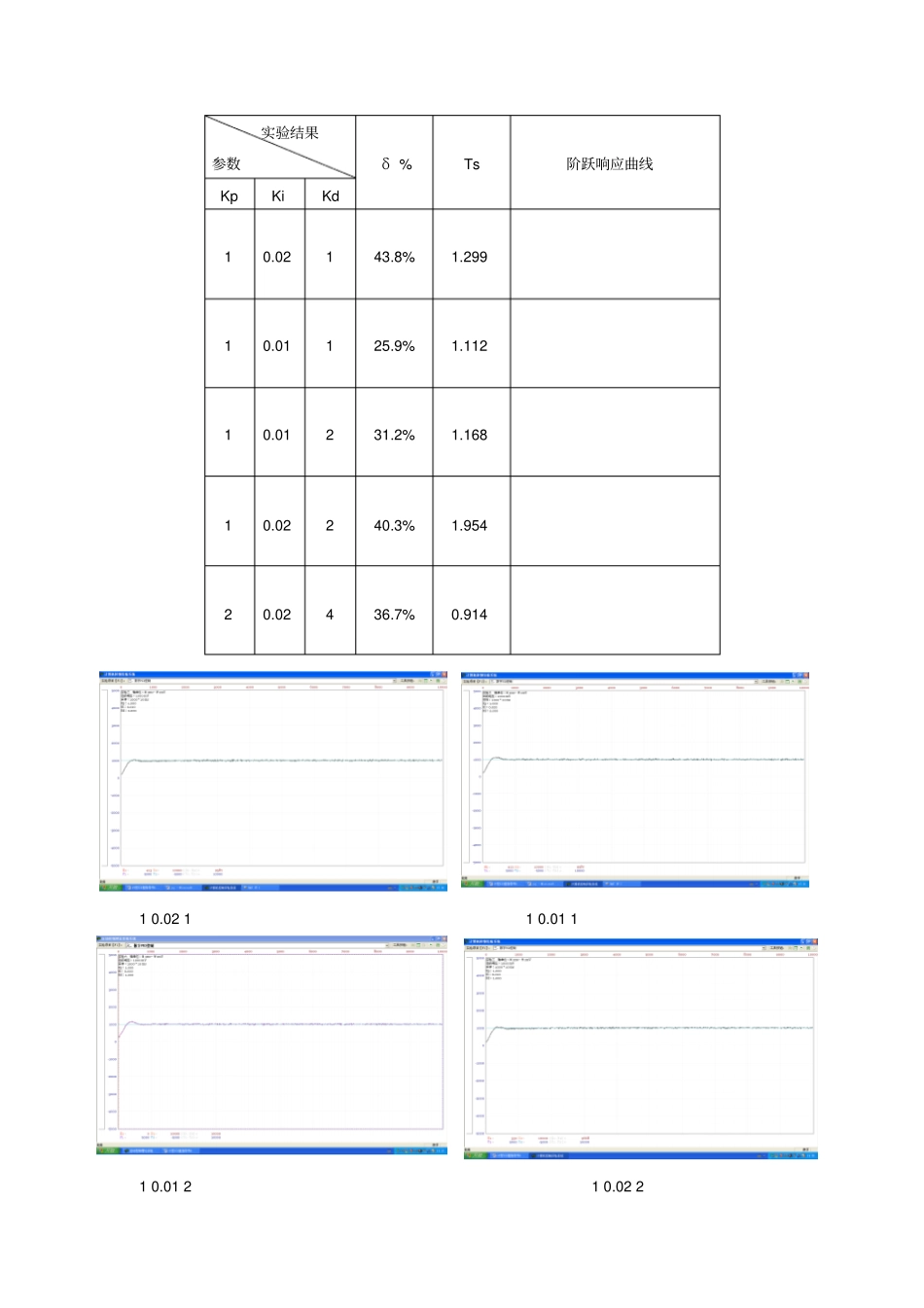
实验三数字PID控制一、实验目的1.研究PID控制器的参数对系统稳定性及过渡过程的影响。2.研究采样周期T对系统特性的影响。3.研究I型系统及系统的稳定误差。二、实验仪器1.EL-AT-III型计算机控制系统实验箱一台2.PC计算机一台三、实验内容1.系统结构图如3-1图。图3-1系统结构图图中Gc(s)=Kp(1+Ki/s+Kds)Gh(s)=(1-e-TS)/sGp1(s)=5/((0.5s+1)(0.1s+1))Gp2(s)=1/(s(0.1s+1))2.开环系统(被控制对象)的模拟电路图如图3-2和图3-3,其中图3-2对应GP1(s),图3-3对应Gp2(s)。图3-2开环系统结构图1图3-3开环系统结构图23.被控对象GP1(s)为“0型”系统,采用PI控制或PID控制,可系统变为“I型”系统,被控对象Gp2(s)为“I型”系统,采用PI控制或PID控制可使系统变成“II型”系统。4.当r(t)=1(t)时(实际是方波),研究其过渡过程。5.PI调节器及PID调节器的增益Gc(s)=Kp(1+K1/s)=KpK1((1/k1)s+1)/s=K(Tis+1)/s式中K=KpKi,Ti=(1/K1)不难看出PI调节器的增益K=KpKi,因此在改变Ki时,同时改变了闭环增益K,如果不想改变K,则应相应改变Kp。采用PID调节器相同。6.“II型”系统要注意稳定性。对于Gp2(s),若采用PI调节器控制,其开环传递函数为G(s)=Gc(s)·Gp2(s)=K(Tis+1)/s·1/s(0.1s+1)为使用环系统稳定,应满足Ti>0.1,即K1<107.PID递推算法如果PID调节器输入信号为e(t),其输送信号为u(t),则离散的递推算法如下:u(k)=u(k-1)+q0e(k)+q1e(k-1)+q2e(k-2)其中q0=Kp(1+KiT+(Kd/T))q1=-Kp(1+(2Kd/T))q2=Kp(Kd/T)T--采样周期四、实验步骤1.连接被测量典型环节的模拟电路(图3-2)。电路的输入U1接A/D、D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输入。检查无误后接通电源。2.启动计算机,双击桌面“计算机控制实验”快捷方式,运行软件。3.测试计算机与实验箱的通信是否正常,通信正常继续。如通信不正常查找原因使通信正常后才可以继续进行实验。4.在实验项目的下拉列表中选择实验三[数字PID控制],鼠标单击鼠标单击按钮,弹出实验课题参数设置窗口。5.输入参数Kp,Ki,Kd(参考值Kp=1,Ki=0.02,kd=1)。6.参数设置完成点击确认后观察响应曲线。若不满意,改变Kp,Ki,Kd的数值和与其相对应的性能指标p、ts的数值。7.取满意的Kp,Ki,Kd值,观查有无稳态误差。8.断开电源,连接被测量典型环节的模拟电路(图3-3)。电路的输入U1接A/D、D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输入,将纯积分电容的两端连在模拟开关上。检查无误后接通电源。9.重复4-7步骤。10.计算Kp,Ki,Kd取不同的数值时对应的p、ts的数值,测量系统的阶跃响应曲线及时域性能指标,记入表中:实验结果参数δ%Ts阶跃响应曲线KpKiKd10.02143.8%1.29910.01125.9%1.11210.01231.2%1.16810.02240.3%1.95420.02436.7%0.91410.02110.01110.01210.02220.024五、实验报告1.画出所做实验的模拟电路图。2.当被控对象为Gp1(s时)取过渡过程为最满意时的Kp,Ki,Kd,画出校正后的Bode图,查出相稳定裕量和穿越频率c。3.总结一种有效的选择Kp,Ki,Kd方法,以最快的速度获得满意的参数。先通过改变Kp的值,使Kp满足要求,再改变Ki,最后是Kd,通过这样一次改变参数的方法可以很快的达到满意的效果。参数整定(试凑法)增大比例系数Kp,一般加快系统响应,在有静差的情况下有利于减小静差,但过大的比例系数会使系统有较大超调,并产生震荡,使稳定性变坏;增大积分时间Ti,有利于减小超调,减小震荡,使系统更加稳定,但系统静差的消除将随之减慢;增大微分时间Td,亦有利于加快系统响应,使超调亮减小,稳定性增加,但对系统的扰动抑制能力减弱,对扰动有较敏感的响应;另外,过大的微分系数也将使得系统的稳定性变坏。实验六大林算法一、实验目的1.掌握大林算法的特点及适用范围。2.了解大林算法中时间常数T对系统的影响。二、实验仪器1.EL-AT-III型计算机控制系统实验箱一台2.PC计算机一台三、实验内容1.实验被控对象的构成:(1)惯性环节的仿真电路及传递函数G(S)=-2/(T1+1)T1=0.2(2)纯延时环节的构成与传递函数G(s)=e-N=采样周期N为正整...