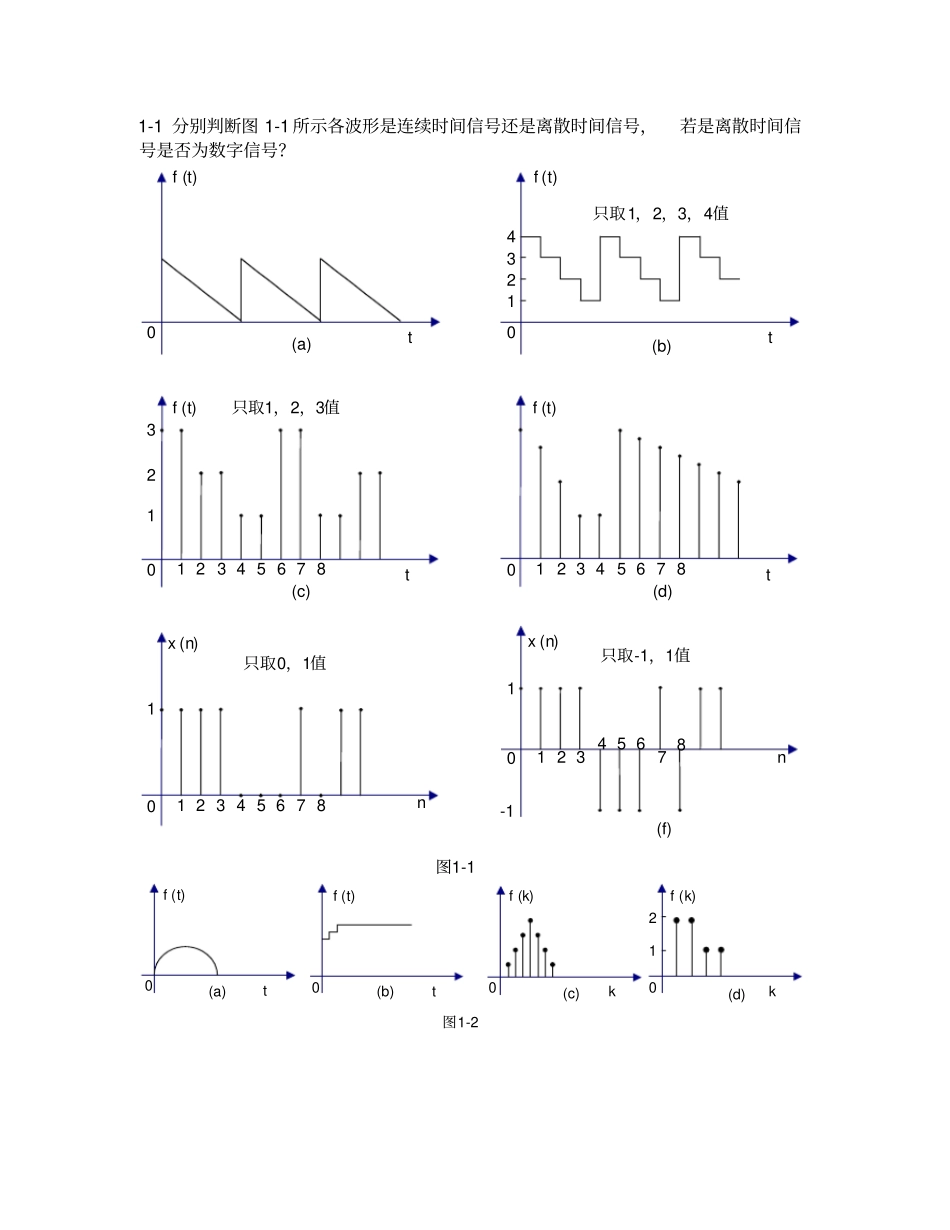
1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?(b)图1-1t0f(t)(a)t0f(t)1234只取1,2,3,4值t0f(t)(c)12312345678只取1,2,3值t0f(t)(d)12345678n0(f)112345678只取0,1值x(n)n0112345678只取-1,1值x(n)-1图1-2t0f(t)(a)t0f(t)(b)k0f(k)(c)k0f(k)(d)12解信号分类如下:))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d21c21b21a21图1-1所示信号分别为(a)连续信号(模拟信号);(b)连续(量化)信号;(c)离散信号,数字信号;(d)离散信号;(e)离散信号,数字信号;(f)离散信号,数字信号。1-2分别判断下列各函数式属于何种信号?(重复1-1题所示问)(1))sin(teat;(2)nTe;(3))cos(n;(4)为任意值)(00)sin(n;(5)221。解由1-1题的分析可知:(1)连续信号;(2)离散信号;(3)离散信号,数字信号;(4)离散信号;(5)离散信号。1-3分别求下列各周期信号的周期T:(1))30t(cos)10t(cos;(2)j10te;(3)2)]8t(5sin[;(4)为整数)(n)TnTt(u)nTt(u)1(0nn。解判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。(1)对于分量cos(10t)其周期5T1;对于分量cos(30t),其周期15T2。由于5为21TT、的最小公倍数,所以此信号的周期5T。(2)由欧拉公式)t(jsin)t(cosetj即)10t(jsin)10t(cosej10t得周期5102T。(3)因为)16t(cos2252252)16t(cos125)8t(5sin2所以周期8162T。(4)由于原函数2)T(2ntT)12n(,11)T(2nt1,2nTn为正整数其图形如图1-3所示,所以周期为2T。t0f(t)-11T2T3T4T⋯图1-31-4对于教材例1-1所示信号,由f(t)求f(-3t-2),但改变运算顺序,先求f(3t)或先求f(-t),讨论所得结果是否与原例之结果一致。解原信号参见例1-1,下面分别用两种不同于例中所示的运算顺序,由f(t)的波形求得f(-3t-2)的波形。两种方法分别示于图1-4和图1-5中。tf(3t)103132方法一:倍乘f(-3t)103231反褶tf(-3t-2)10132t32左移tf(-t)10方法二:反褶f(-3t)103231倍乘tf(-3t-2)10132t32左移2-1图1-4图1-51-5已知f(t),为求)(0attf应按下列那种运算求得正确结果(式中at,0都为正值)?(1))(atf左移0t;(2))(atf右移0t;(3))(atf左移at0;(4))(atf右移at0。解(1)因为)(atf左移0t,得到的是)()(00atatfttaf,所以采用此种运算不行。(2)因为)(atf右移0t,得到的是)()(00atatfttaf,所以采用此运算不行。(3)因为)(atf左移at0,得到的是)()(00tatfattaf,所以采用此运算不行。(4)因为)(atf右移at0,得到的是)()(00attfattaf,所以采用此运算不行。1-6绘出下列各信号的波形:(1))8sin()sin(211tt;(2))8sin()sin(1tt。解(1)波形如图1-6所示(图中)8sin()sin(211)(tttf)。00.511.500.511.52f(t)f(t)82t82t图1-6图1-7(2)波形如图所示1-7(图中)8sin()sin(1)(tttf)。1-7绘出下列各信号的波形:(1))4sin()()(tTTtutu;(2))4sin()2()(2)(tTTtuTtutu。解)4sin(tT的周期为2T。(1)波形如图1-8(a)所示(图中)4sin()()(tTTtutu)。在区间T,0,内,包含有)4sin(tT的两个周期。01f(t)t图1-8-12TT01f(t)-1T2T(a)(b)t(2)波形如图1-8(b)所示(图中)4sin()2()(2)(tTTtuTtutu)。在区间TT2,内是)4sin(tT,相当于将)4sin(tT倒像。1-8试将教材中描述图1-15波形的表达式(1-16)和(1-17)改用阶越信号表示。解表达式(1-16)为)(0)(ttaatateeetftttt000当当这是一个分段函数。若借助阶越信号,则可将其表示为)()()(][)()(e)(0)(0)(000ttuetuettueettututfttaatttaatat]表达式(1-17)为)()1(1)1(1)0()1(1)(0)(00tteaeatteadfttaatatt借助阶越信号,可将其表示为)(]1[1)()(1)(]1[1)1(1)]()()[1(1)(0)(0)(000ttueatueaattueaeattutueadfttaatttaatatt1-9粗略绘出下列各函数式的波形图:(1))()2()(tuetft;(2))()63()(2tueetftt;(3))()55()(3tuee...