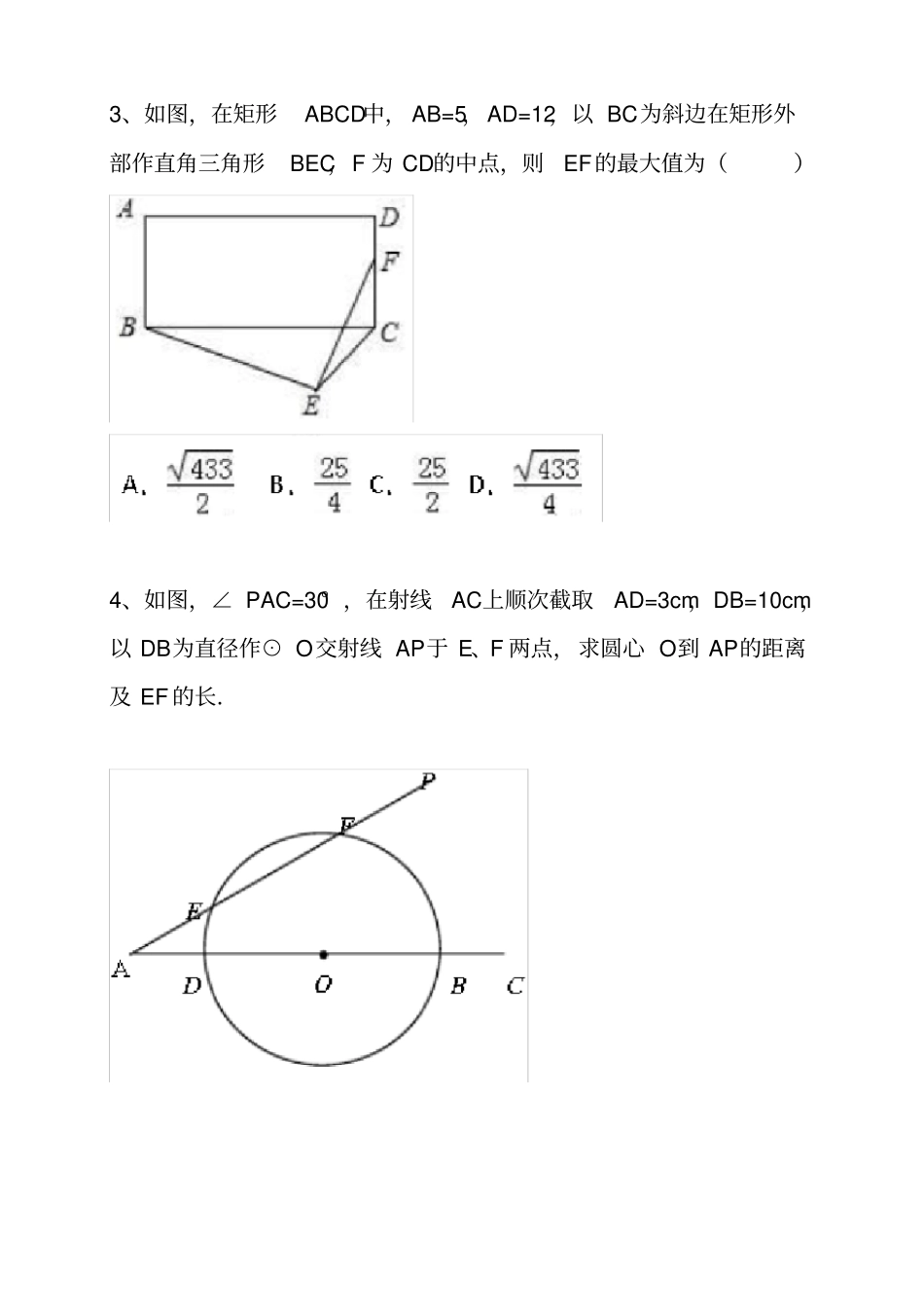
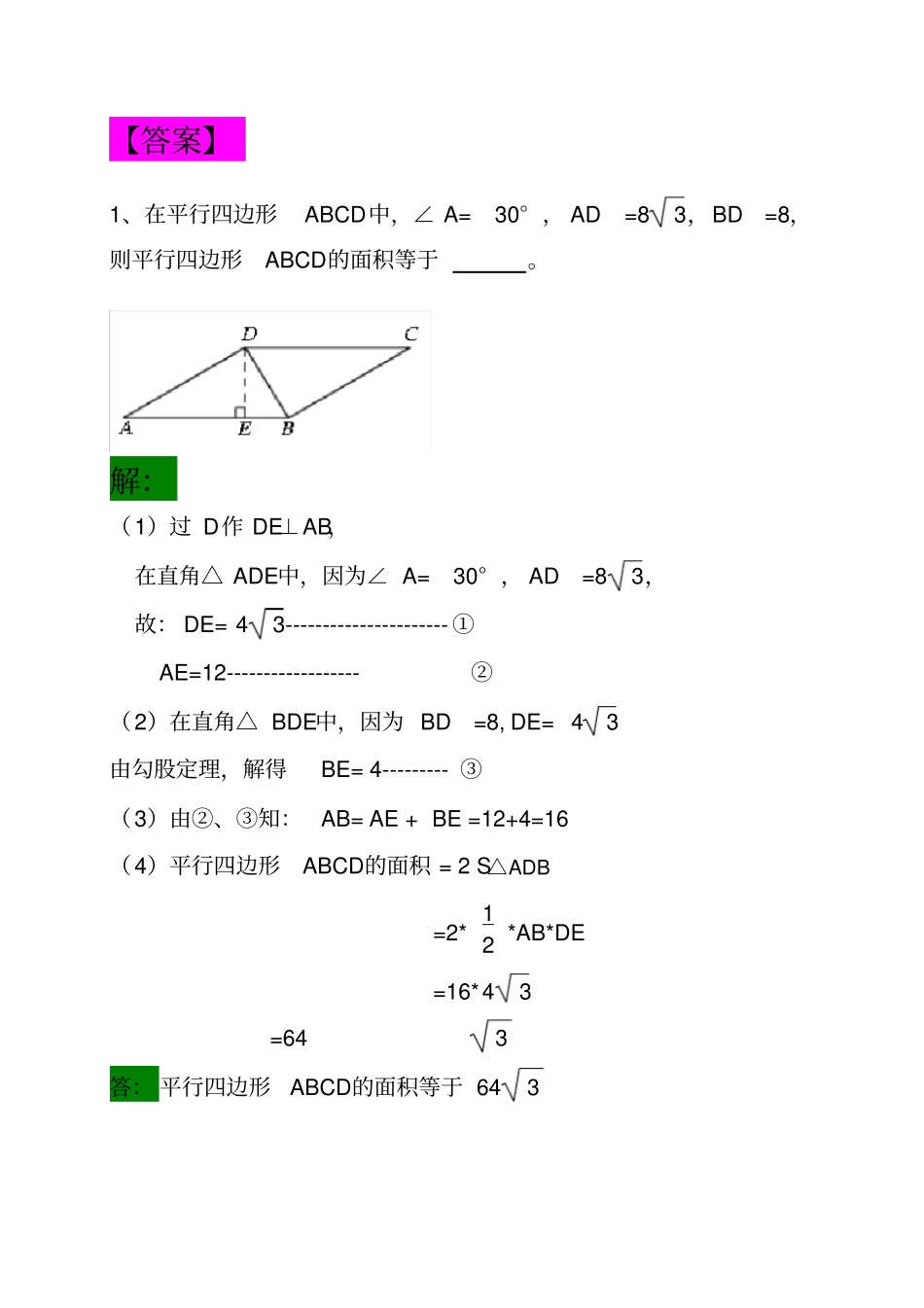
【编著】黄勇权【第一组题型】1、在平行四边形ABCD中,∠A=30°,AD=83,BD=8,则平行四边形ABCD的面积等于。2、如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,且AF⊥DE,若AB=8,AD=6,则CF的长为。初中数学几何中考经典试题集3、如图,在矩形ABCD中,AB=5,AD=12,以BC为斜边在矩形外部作直角三角形BEC,F为CD的中点,则EF的最大值为()4、如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.【答案】1、在平行四边形ABCD中,∠A=30°,AD=83,BD=8,则平行四边形ABCD的面积等于。解:(1)过D作DE⊥AB,在直角△ADE中,因为∠A=30°,AD=83,故:DE=43----------------------①AE=12------------------②(2)在直角△BDE中,因为BD=8,DE=43由勾股定理,解得BE=4---------③(3)由②、③知:AB=AE+BE=12+4=16(4)平行四边形ABCD的面积=2S△ADB=2*12*AB*DE=16*43=643答:平行四边形ABCD的面积等于6432、如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,且AF⊥DE,若AB=8,AD=6,则CF的长为。解:(1)因为ABCD是矩形,由勾股定理,解得对角线AC=AD2+DC2=62+82=10----①(2)E是边AB的中点,且AB=8,所以:AE=4-------------②(3)在直角△ADE中,由勾股定理,解得DE=AD2+AE2=62+42=213------------③(4)在直角△ADE中,△ADE的面积=12AD*AE又因为AF⊥DE,△ADE的面积=12DE*AF故:AD*AE=DE*AF分别将AD、AE、DE的值代入,即:6*4=213*AF解得:AF=121313(5)CF=AC-AF=10-121313答:CF的长为10-1213133、如图,在矩形ABCD中,AB=5,AD=12,以BC为斜边在矩形外部作直角三角形BEC,F为CD的中点,则EF的最大值为()4、如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.解:(1)过O作AP的垂线,连接OE、OF。(2)AO=AD+12BD=3+5=8又∠PAC=30°,△AOG为直角三角形故:OG=12OA=4答:圆心O到AP的距离为4.(3)OE、OF是圆O的半径,所以:OE=OF,则△OEF为等腰三角形又OG⊥EF,则OG是EF的中线。得:EG=FG----------------①在RT△OEG中,OE=12DB=5,OG=4由勾股定理,解得:EG=3--------②(4)由①、②得EF=2EG=6答:EF的长为6【第二组题型】5、如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是()6、如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.(1)求证:四边形ABCD是矩形;(2)若∠AOB:∠ODC=4:3,求∠ADO的度数.7、在梯形ABCD中,AD∥BC,EA⊥AD,M是AE上一点,∠BAE=∠MCE,∠MBE=45°(1)求证:BE=ME(2)若AB=7,求MC的长8、如图,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F,若CF⊥AD,AB=2,求CD的长【答案】5、如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是()解:(1)因为CA2+AB2=122+52=169BC2=132=169所以:BC2=CA2+AB2由勾股定理知,△ABC为RT△,且∠A=90°-----①又因为圆O与△ABC相切,所以:OF=OE------------------------------②∠AFO=∠AEO=90°--------------------③由①、②、③知,AEOF是正方形。(2)连接OA、OB、OC,且设OA=OB=OC=r因为OE⊥AC,所以△AOC面积=12OE*AC=12*r*12=6r------④同理:△AOB面积=52r-----------------------⑤△BOC面积=132r------------------------⑥由④⑤⑥得:△ABC面积=△AOC面积+△AOB面积+△BOC面积=15r--------------⑦(3)又因为△ABC为RT△,且∠A=90°△ABC面积=12AB*AC=30--------------⑧由⑦⑧得:15r=30解得:r=2(4)AEOF是正方形,所以阴影部分面积=r2=4答:则阴影部分(即四边形AEOF)的面积是46、如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.(1)求证:四边形ABCD是矩形;(2)若∠AOB:∠ODC=4:3,求∠ADO的度数.解:(1)证明【第一步】因为AO=OC,BO=OD所以交点O平分对角线线AC、BD则四边形ABCD为平行四边形。---①【第二步...