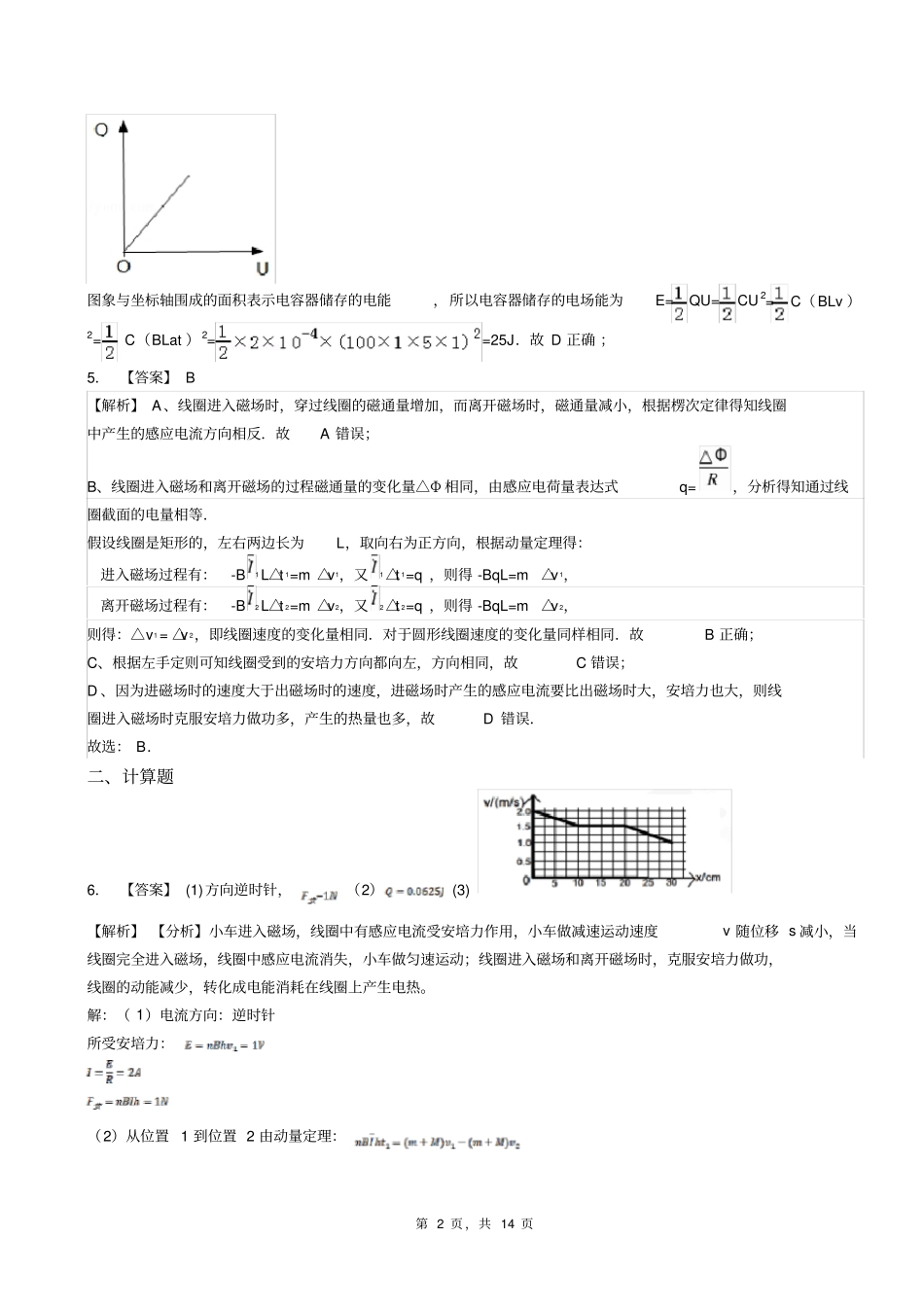
第1页,共14页安培力的冲量(参考答案)一、选择题1.【答案】C2.【答案】AD【解析】金属棒M向右运动后,穿过MN与导轨组成的闭合回路中的磁通量减小,根据楞次定律可得回路内产生顺时针方向的电流(俯视),A正确;两棒最后匀速时,电路中无电流,即1122BLvBLv,解得212vv,选取水平向右为正方向,对M、N分别利用动量定理可得:对N有2NFtmv安;对M有10MFtmvmv安,又知道导轨宽度是2倍关系,故2MNFF安安,联立解得11/vms,22/vms,B错误;根据能量守恒定律可得222012111222mvQmvmv,解得0.1QJ,C错误;在N加速过程中,由动量定理得20BILtmv,电路中的电流EIR,据法拉第电磁感应定律有Et,其中磁通量变化量BS,联立以上各式,得20.5/Sms,D正确【点睛】本题是双轨双棒问题,要注意分析两棒的运动过程,明确两棒都匀速运动时它们的感应电动势是相等的,知道动量定理是求电磁感应中电量常用的思路.3.【答案】C【解析】A.金属棒运动到a处时,有E=BLva,I=E/(R+r),安培力:F=BIL=,由牛顿第二定律得加速度:a=F/m=,故A错误;B.金属棒运动到b处时,由右手定则判断知,通过电阻的电流方向由Q指向N,故B错误;C.金属棒在a→b过程中,通过电阻的电荷量,同理,在b→c的过程中,通过电阻的电荷量,由于△Φab=△Φbc,可得q1=q2.故C正确;D.在b→c的过程中,对金属棒运用动量定理得:,而∑v△t=lbc,同理,在a→c的过程中,对金属棒运用动量定理得:,而∑v△t′=lac,因lac=2lbc,因此va=2vb,故D错误。故选:C.4.【答案】BD。【解析】解:A、设经过时间△t时,金属棒的速度为v,根据动量定理可得:(mgsin30°+F)△t﹣BIL△t=m?△v,金属棒切割磁感线产生电动势变化△E=BL△v,电容器的电量变化量Q=I△t=CBL?△v所以有:(mgsin30°+F)△t﹣BL?CBL△v=m△v,又加速度定义式a=,可得加速度a=,为定值,所以金属棒做匀加速直线运动。故A错误;B、由a=,代入数据解得a=5m/s2.对金属棒,应用牛顿第二定律有mgsin30°+F﹣BIL=ma,解得I=0.1A,由右手定则知,金属棒运动过程中通过其电流方向从b到a,故B正确;C、通过电容器的电量Q=It=1×1C=1C,故C错误;D、电容器所带的电荷量与电容器两端电压关系图象如图所示,第2页,共14页图象与坐标轴围成的面积表示电容器储存的电能,所以电容器储存的电场能为E=QU=CU2=C(BLv)2=C(BLat)2==25J.故D正确;5.【答案】B【解析】A、线圈进入磁场时,穿过线圈的磁通量增加,而离开磁场时,磁通量减小,根据楞次定律得知线圈中产生的感应电流方向相反.故A错误;B、线圈进入磁场和离开磁场的过程磁通量的变化量△Φ相同,由感应电荷量表达式q=,分析得知通过线圈截面的电量相等.假设线圈是矩形的,左右两边长为L,取向右为正方向,根据动量定理得:进入磁场过程有:-B1L△t1=m△v1,又1△t1=q,则得-BqL=m△v1,离开磁场过程有:-B2L△t2=m△v2,又2△t2=q,则得-BqL=m△v2,则得:△v1=△v2,即线圈速度的变化量相同.对于圆形线圈速度的变化量同样相同.故B正确;C、根据左手定则可知线圈受到的安培力方向都向左,方向相同,故C错误;D、因为进磁场时的速度大于出磁场时的速度,进磁场时产生的感应电流要比出磁场时大,安培力也大,则线圈进入磁场时克服安培力做功多,产生的热量也多,故D错误.故选:B.二、计算题6.【答案】(1)方向逆时针,(2)(3)【解析】【分析】小车进入磁场,线圈中有感应电流受安培力作用,小车做减速运动速度v随位移s减小,当线圈完全进入磁场,线圈中感应电流消失,小车做匀速运动;线圈进入磁场和离开磁场时,克服安培力做功,线圈的动能减少,转化成电能消耗在线圈上产生电热。解:(1)电流方向:逆时针所受安培力:(2)从位置1到位置2由动量定理:第3页,共14页其中联立得到求得从位置2到位置3由动量定理:求得(1分)从位置2到位置3由能量转化得:求得(3)对线框和车进入过程,设位移为x由动量定理可求得表达式,速度随位移线性减小,在位置1和位置2之间,小车匀速运动,之后同理分析得速度又随位移线性减小,故得到如下图7.【答案】(1)线圈匀速运动的速率v为;(2)穿过磁场区域过程中,线圈中产生的热量Q为mg(b+h)﹣...