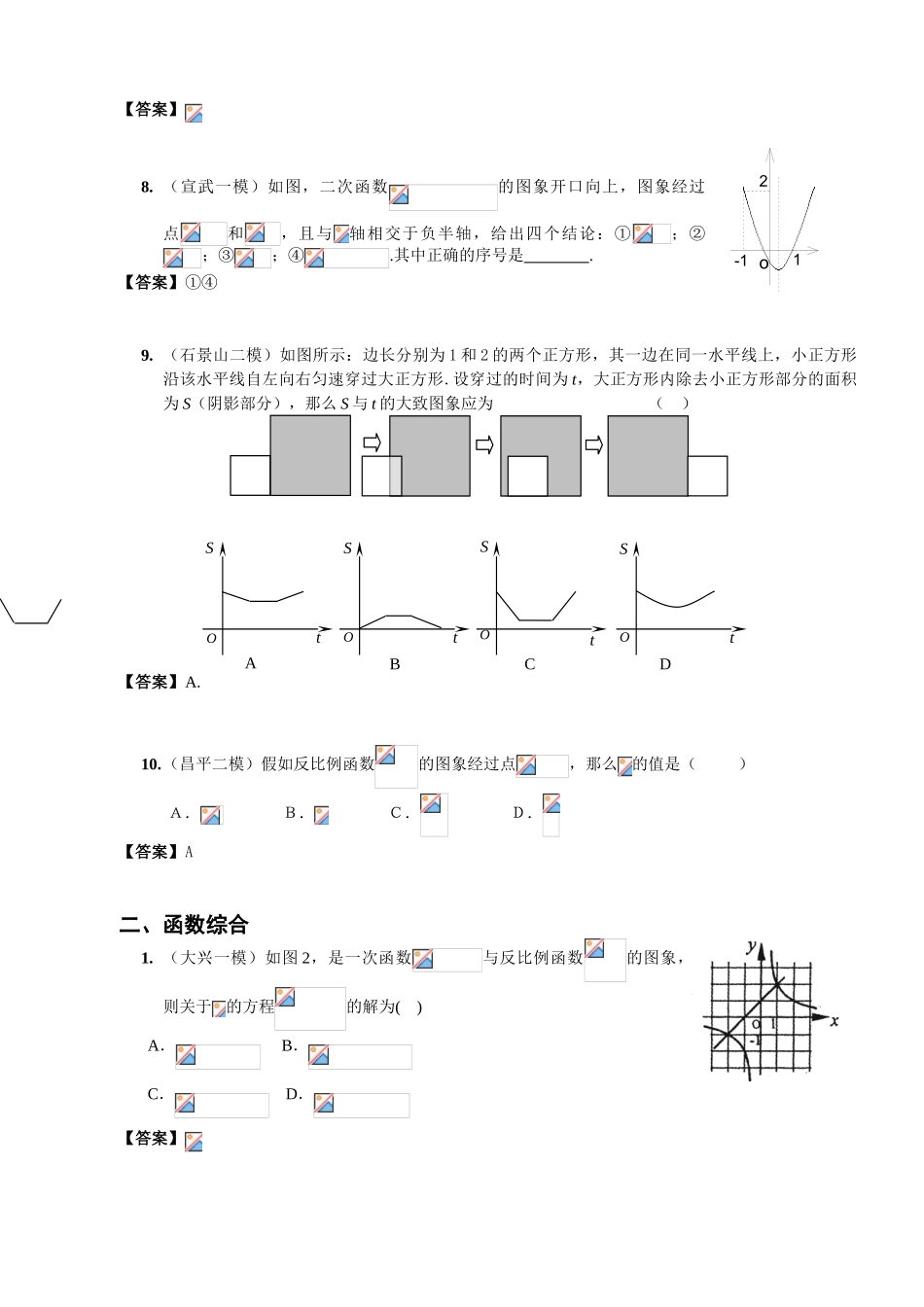
2024-2024年中考模拟分类汇编⑷函数函数一、函数基本知识1.(海淀一模)函数中,自变量的取值范围是.【答案】2.(朝阳一模)函数中,自变量的取值范围是()且且【答案】3.(朝阳一模)如图,抛物线,,下列关系中正确的是()【答案】A4.(大兴一模)函数自变量的取值范围是()【答案】B5.(大兴一模)若反比例函数的图象上有两点,,则_____(填“”或“”或“”).【答案】.6.(丰台一模)写出一个图像在第二、第四象限的反比例函数的解析式.【答案】(答案不惟一)7.(宣武一模)已知一次函数(,是常数,且),与的部分对应值如表所示,那么的值等于().(A)(B)(C)(D)-1011-1【答案】8.(宣武一模)如图,二次函数的图象开口向上,图象经过点和,且与轴相交于负半轴,给出四个结论:①;②;③;④.其中正确的序号是.【答案】①④9.(石景山二模)如图所示:边长分别为1和2的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形.设穿过的时间为t,大正方形内除去小正方形部分的面积为S(阴影部分),那么S与t的大致图象应为()【答案】A.10.(昌平二模)假如反比例函数的图象经过点,那么的值是()A.B.C.D.【答案】A二、函数综合1.(大兴一模)如图2,是一次函数与反比例函数的图象,则关于的方程的解为()A.B.C.D.【答案】1o2-1tSODtSOAtSOBtSOC2.(海淀一模)已知一次函数的图象与轴,轴分别交于,直线经过上的三分之一点,且交轴的负半轴于点,假如,求直线的解析式.【答案】 直线与轴,轴交点为,∴两点坐标分别为,∴,∴ 为上的三分之一点,∴点的坐标为或, ∴当是,;当时,, 点在轴的负半轴上,∴点的坐标为或∴直线的解析式为或3.(宣武一模)如图,反比例函数的图象与一次函数的图象交于(1,3)、(,)两点.⑴求反比例函数与一次函数的解析式;⑵根据图象回答:当取何值时,反比例函数的值大于一次函数的值?【答案】⑴点(1,3)在反比例函数图象上,,即.反比例函数解析式为.…………………………………………………1分又点(,)在反比例函数图象上,,即.(,).…………………………………………………………………………2分又点(1,3)和(,)在一次函数图象上,,解得一次函数解析式为.……………………………………………………3分⑵由交点(1,3)和(,)可知:当或时,反比例函数的值大于一次函数的值.………………………5分BAMQ0,bPa,o1-1oyx14.(朝阳一模)已知、是关于的一元二次方程的两个实数根,其中为非负整数,点,是一次函数与反比例函数图象的交点,且、为常数.⑴求的值;⑵求一次函数与反比例函数的解析式.【答案】⑴依题意,得……………………………………1分解得且. 为非负整数,∴.…………………………………………………2分⑵当时,原方程化为.解得.∴,.……………………………………………3分把,和代入,得.∴一次函数的解析式是.…………………………………………4分把,代入,得.∴反比例函数的解析式是.………………………………………5分5.(丰台一模)一次函数的图象经过点,且分别与轴、轴交于点、.点在轴正半轴上运动,点在轴正半轴上运动,且.⑴求的值,并在给出的平面直角坐标系中画出该一次函数的图象;⑵求与满足的等量关系式.【答案】⑴一次函数的图象经过点(1,4),则,,…………………………………………分∴.该函数的图象见右图:…………………………………………分⑵函数的图象与轴、轴的交点分别为、,………………………分 ,设交点为,则,∴△△,……………………分∴,即∴.………………………………分6.(朝阳一模)如图,在矩形中,,,点处有一动点以的速度由向运动,同时点处也有一动点以的速度由向运动,设运动的时间为,四边形的面积为,求与的函数关系式及自变量的取值范围.【答案】依题意,得,.…………1分在矩形中,,,,∴,.…………………………………………………2分∴四边形的面积=即.…………………………………………………………………4分自变量的取值范围是.……………………………………………5分7.(朝阳一模)...