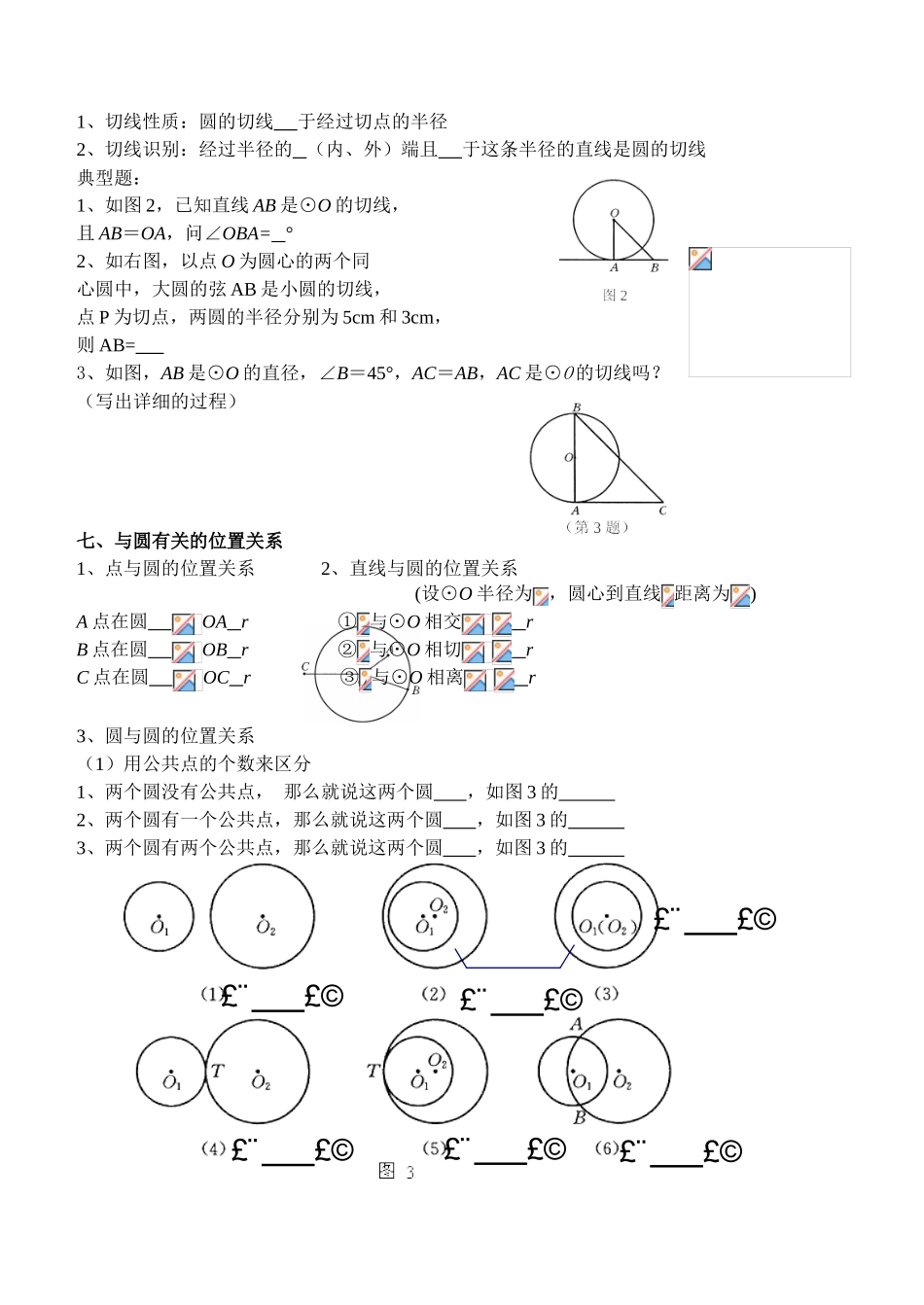
2024年备战中考复习系列《图形的认识》2024-2024年中考专题复习图形的认识之圆资料内容提要一、确定一个圆有两要素,一是,二是,圆心确定、半径确定;圆既是对称图形,又是对称图形;它的对称中心是,对称轴是,有条对称轴。二、在同圆或等圆中,两个圆心角、两条弧、两条弦三组量之间,假如有一组量相等,那么,它们所对应的其它量也相等。典型题:如图,AB、CD是⊙O的两条弦①若AB=CD,则有=,=②若AB=CD,则有=,=③若∠AOB=∠COD,则有=,=三、在在同圆或等圆中,同弧或等弧所对圆周角,相等的圆周角所对的弧,同弧或等弧所对圆周角是其所对的圆心角的。典型题:1、如图,AB、AC、BC都是⊙O的弦,∠CAB=∠CBA,∠COB与∠COA相等吗?为什么?2、如图,∠A是⊙O的圆周角,∠A=30°,则∠BOC=°,∠OBC=°四、半圆或直径所对的圆周角都是°,90°的圆周角所对的弦是圆是。典型题:1、如图,AB是⊙O的直径,∠DCB=30°,则∠ACD=°,∠ABD=°2、如图,⊙O的直径AB=10,弦BC=5,∠B=°五、垂直于弦的直径平分这条弦,并且平弦所对的弧。即:如图,若AB⊥CD,则有APPB,︵AC︵CB,AD=典型题:如上图,若CD=10,AB=8,求PC的长?六、切线1、切线性质:圆的切线于经过切点的半径2、切线识别:经过半径的(内、外)端且于这条半径的直线是圆的切线典型题:1、如图2,已知直线AB是⊙O的切线,且AB=OA,问∠OBA=°2、如右图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,两圆的半径分别为5cm和3cm,则AB=3、如图,AB是⊙O的直径,∠B=45°,AC=AB,AC是⊙O的切线吗?(写出详细的过程)七、与圆有关的位置关系1、点与圆的位置关系2、直线与圆的位置关系(设⊙O半径为,圆心到直线距离为)A点在圆OAr①与⊙O相交rB点在圆OBr②与⊙O相切rC点在圆OCr③与⊙O相离r3、圆与圆的位置关系(1)用公共点的个数来区分1、两个圆没有公共点,那么就说这两个圆,如图3的2、两个圆有一个公共点,那么就说这两个圆,如图3的3、两个圆有两个公共点,那么就说这两个圆,如图3的£¨£©£¨£©£¨£©£¨£©£¨£©£¨£©(2)用数量关系来区别:设两圆的半径分别为、,圆心距为:1、用数轴表示圆与圆的位置与圆心距d之间的对应关系(在数轴上填出圆心距d各在区域中对应圆与圆的位置名称)2、根据数轴填表两圆的位置关系数量关系及其识别方法外离外切相交内切内含典型题:1、已知⊙O的半径为6,A为线段PO的中点,当OP=10时,点A与⊙O的位置关系为()A.在圆上B.在圆外C.在圆内D.不确定2、圆最长弦为12,假如直线与圆相交,且直线与圆心的距离为,那么()A.B.C.D.3、已知圆⊙O1和⊙O2的半径的6cm和8cm,当O1O2=12cm时,⊙O1和⊙O2的位置关系为()A.外切B.相交C.内切D.内含4、两圆半径和为24cm,半径之比为1:2,圆心距为8cm,则两圆的位置关系为()A.外离B.相交C.内切D.外切八、切线长定理:从圆一点可以引圆的条切线,它们的切线长.这一点和圆心的连线这两条切线的角.即:如右图,PA,PB分别为⊙O的切线,切点分别为A、B,则PAPB,PO平分∠典型题:1、如下图,PA,PB分别为⊙O的切线,切点分别为A、B,∠P=60°PA=10cm,那么AB的长为2、如图,PA,PB分别为⊙O的切线,AC为直径,切点分别为A、B,∠P=70°,则∠C=3、如上图,PA,PB分别为⊙O的切线,切点分别为A、B,PA=10,在劣弧︵AB上任取一点C,过C作⊙O的切线,分别交PA,PB于D,E,则△PDE的周长是九、圆有关的计算(1)弧长的计算假如弧长为l,圆心角度数为n,圆的半径为r,那么,弧长半径r圆心角度数n弧长l1036°52120°12(圆周率用表示即可)(2)扇形面积计算:方法一:假如已知扇形圆心角为n,半径为r,那么,扇形面积方法二:假如已知扇形弧长为l,半径为r,那么,扇形面积半径r圆心角度数n弧长l扇形面积1036°66264(3)圆锥的侧面积与表面积1、如图1:为圆锥的为,为圆锥的为,为圆锥的底面为,由勾股定理可得:、、之间的关系为:2、如图2:圆锥的侧面展开后一个:圆锥的母线是扇形的而扇形的弧长恰好是圆锥底面的。故:圆锥的侧面积就是圆锥的侧面展开后的扇形的圆锥的表面积=+3、看图1、填表:底面积底面圆的周长侧面积表(全)面积3551368(圆周率用表示即可)