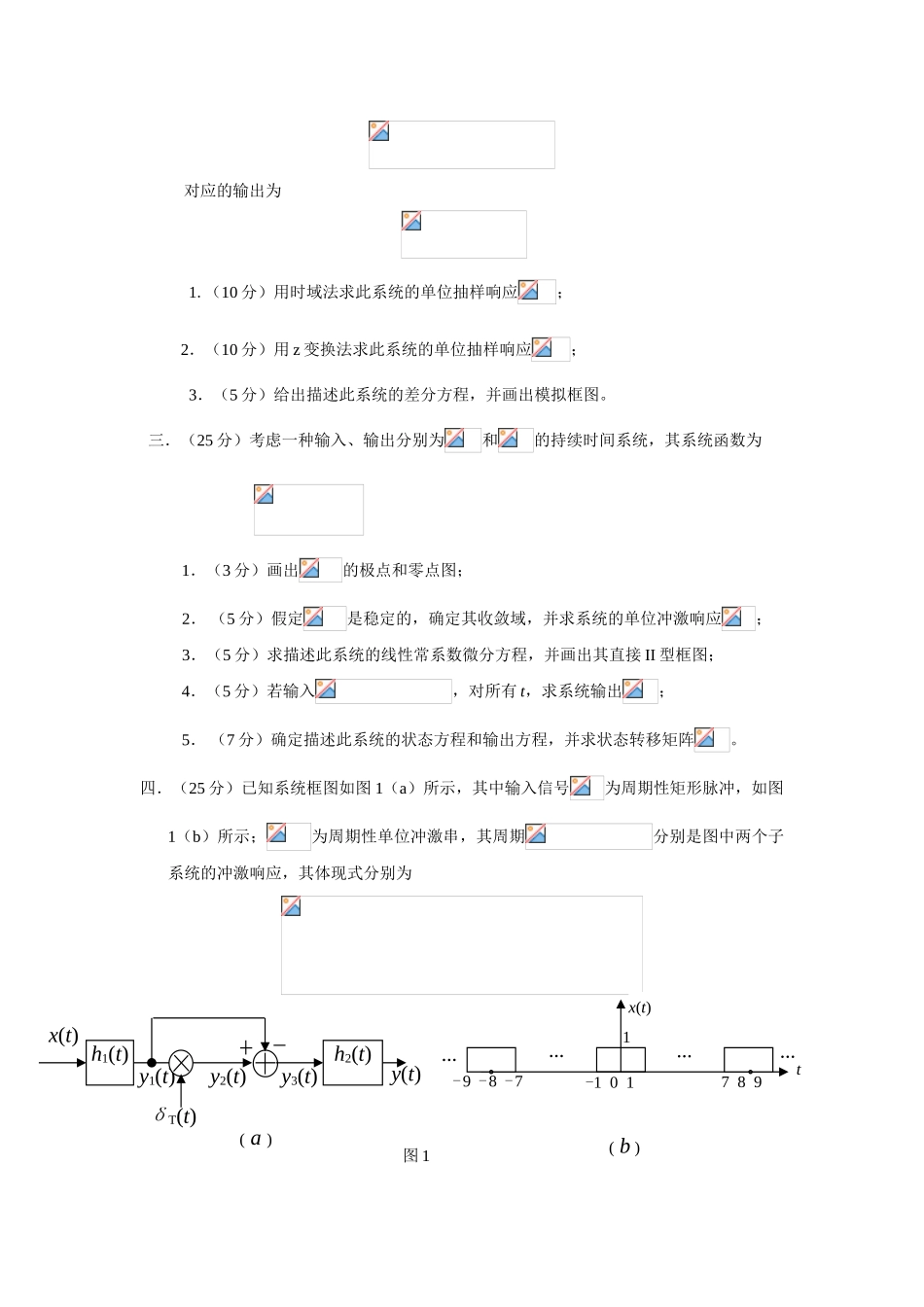
一.(30分)简述题(每题3分)1.一种LTI系统有多种描述措施,试给出五种措施,并指出它们之间的联络。2.一种确定信号在频域用傅里叶变换表达,试按信号在时域是周期、非周期、持续、离散,分别写出对应形式的傅里叶变换。离散傅里叶变换(DFT)是其中一种形式吗?3.一种存在所有时域的周期信号,假如规定在变换域求其作用于LTI系统的响应,应采用傅里叶变换还是拉氏变换?或者两种变换都可采用?为何?4.若由下列系统函数描述的离散时间系统是稳定的,那它一定是因果的吗?为何?5.根据下列微分方程,能否鉴定该系统是稳定的吗?为何?6.由下式描述的系统是时不变的吗?为何?(式中的,分别表达系统的输入和输出)7.试给出设计数字滤波器的一般环节。8.能否仅根据其频率响应的有限个取样值,确定出该数字滤波器?阐明你的理由。9.怎样保证所设计的FIR数字滤波器具有线性相位?10.分别给出序列线性卷积、圆周卷积和周期卷积的定义,并指出它们间的联络。二.(25分)考虑一种离散时间LTI系统,当其输入为北京理工大学攻读硕士学位硕士入学考试试题机密★启用前试题答案必须书写在答题纸上,在试题和草稿纸上答题无效。科目代码:426科目分号:0111科目名称:信号处理导论注:试题上不准填写准考证号和姓名对应的输出为1.(10分)用时域法求此系统的单位抽样响应;2.(10分)用z变换法求此系统的单位抽样响应;3.(5分)给出描述此系统的差分方程,并画出模拟框图。三.(25分)考虑一种输入、输出分别为和的持续时间系统,其系统函数为1.(3分)画出的极点和零点图;2.(5分)假定是稳定的,确定其收敛域,并求系统的单位冲激响应;3.(5分)求描述此系统的线性常系数微分方程,并画出其直接II型框图;4.(5分)若输入,对所有t,求系统输出;5.(7分)确定描述此系统的状态方程和输出方程,并求状态转移矩阵。四.(25分)已知系统框图如图1(a)所示,其中输入信号为周期性矩形脉冲,如图1(b)所示;为周期性单位冲激串,其周期分别是图中两个子系统的冲激响应,其体现式分别为δT(t)y(t)y3(t)y2(t)y1(t)x(t)h1(t)h2(t)(a)1……-9-8-7789-101……x(t)t(b)图11.(5分)求的频谱的表达式,并画出其频谱图(注明过零点的频率值);2.(5分)求的频谱的表达式,并画出其频谱图;3.(5分)求的表达式(以表达),并画出其频谱图;该频谱会发生混叠吗?为何?4.(5分)写出的表达式(以表达),并画出其频谱图;5.(5分)写出的频谱的表达式,指明对应的原信号有何特点。五.(20分)设有两个实序列和,其长度分别为8192和64,试给出迅速计算和线性卷积的措施环节及其对应的运算量。规定运用基2FFT,同步尽量减少乘法运算次数。六.(25分)有关IIR数字滤波器:1.(15分)给出一般形式的IIR数字滤波器的三种基本构造,即直接型、级联型和并联型,并指出上述三种构造的优缺陷及应用场所。2.(10分)证明采用双线性变换措施设计的IIR数字滤波器与原模拟滤波器具有相类似的特性。一.(30分)简述题(每题5分)11.画出函数的波形,并计算积分值:12.已知,画出下列函数的图形:13.已知LTI系统的输入和输出满足如下关系试确定该系统与否因果、稳定,并阐明理由。14.系统函数,其中,试问无论怎样取值,代表的一定是低通滤波器吗?为何?15.已知序列和,给出和的4点圆周卷积和4点圆周有关的成果。16.运用双线性法,从模拟低通设计数字低通滤波器时,为何要预畸?简朴阐明预畸的作法?二.(25分)已知一种因果LTI离散时间系统的初始条件为,,当输入序列时,其完全响应为规定:1.(8分)系统的零输入响应。北京理工大学攻读硕士学位硕士入学考试试题机密★启用前试题答案必须书写在答题纸上,在试题和草稿纸上答题无效。科目代码:426科目分号:0113科目名称:信号处理导论注:表达数字频率2.(5分)系统函数,并画出其零极点图。3.(5分)判断此系统的频率响应函数与否存在。如存在,请写出其表达式;如不存在,请阐明原因。4.(7分)由写出系统的状态方程的A、B、C、D矩阵。三.(25分)某系统由两个LTI子系统并联而成,其中一种子系统的单位抽样响应...