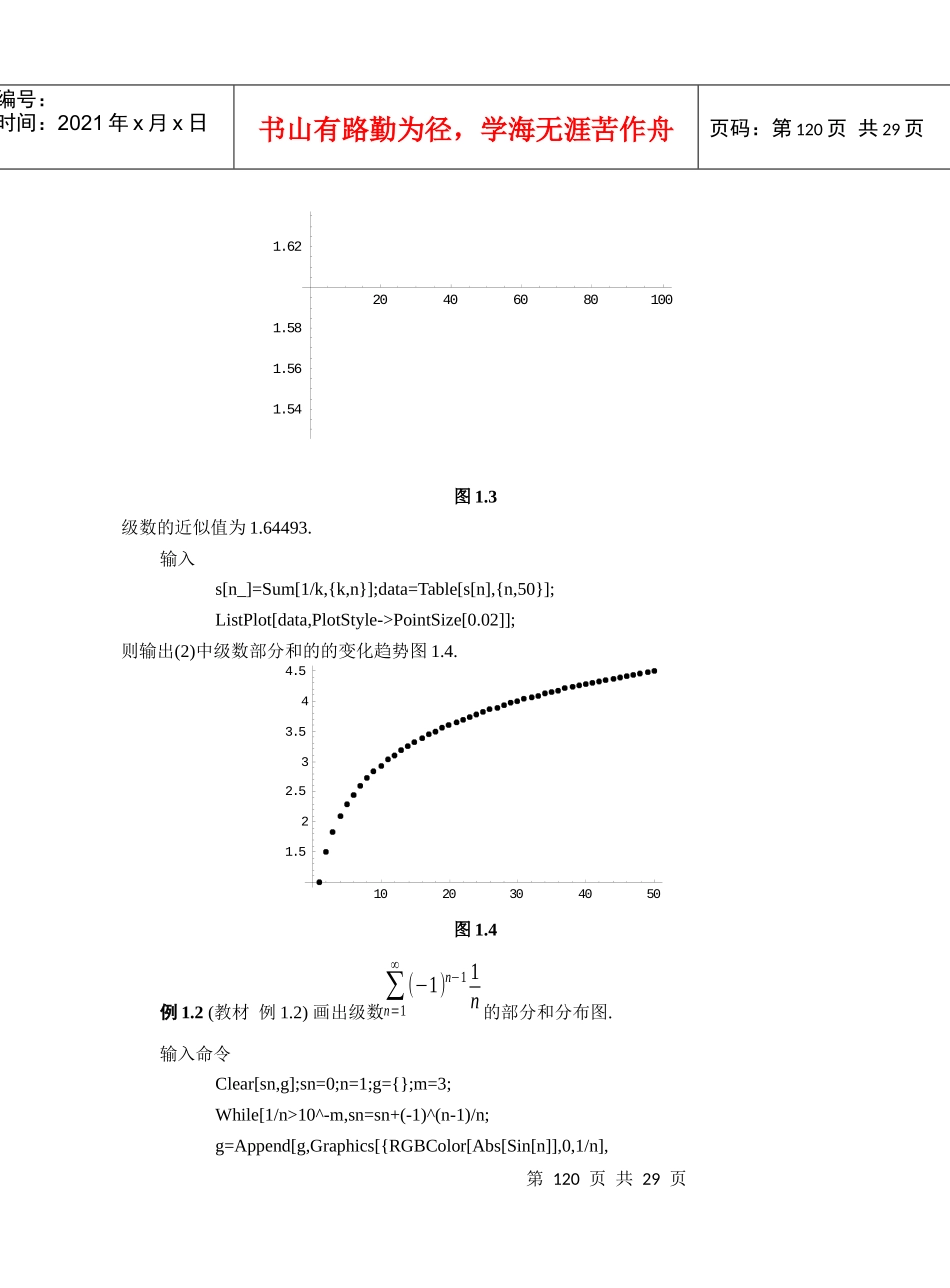
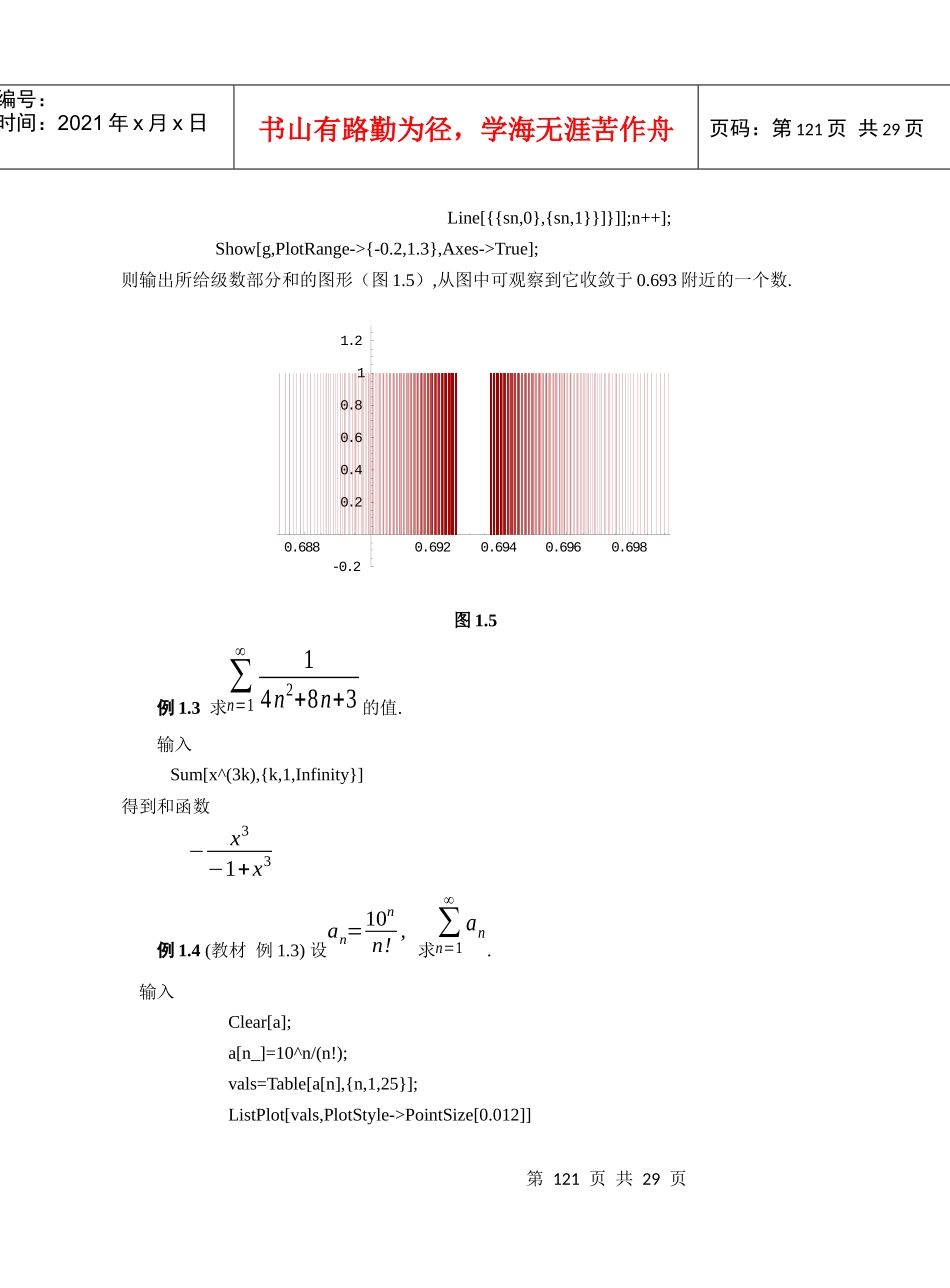
第119页共29页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第119页共29页项目四无穷级数与微分方程实验1无穷级数(基础实验)实验目的观察无穷级数部分和的变化趋势,进一步理解级数的审敛法以及幂级数部分和对函数的逼近.掌握用Mathematica求无穷级数的和,求幂级数的收敛域,展开函数为幂级数以及展开周期函数为傅里叶级数的方法.数项级数例1.1(教材例1.1)(1)观察级数∑n=1∞1n2的部分和序列的变化趋势.(2)观察级数∑n=1∞1n的部分和序列的变化趋势.输入s[n_]=Sum[1/k^2,{k,n}];data=Table[s[n],{n,100}];ListPlot[data];N[Sum[1/k^2,{k,Infinity}]]N[Sum[1/k^2,{k,Infinity}],40]则输出(1)中级数部分和的变化趋势图1.3.第120页共29页第119页共29页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第120页共29页图1.3级数的近似值为1.64493.输入s[n_]=Sum[1/k,{k,n}];data=Table[s[n],{n,50}];ListPlot[data,PlotStyle->PointSize[0.02]];则输出(2)中级数部分和的的变化趋势图1.4.图1.4例1.2(教材例1.2)画出级数∑n=1∞(−1)n−11n的部分和分布图.输入命令Clear[sn,g];sn=0;n=1;g={};m=3;While[1/n>10^-m,sn=sn+(-1)^(n-1)/n;g=Append[g,Graphics[{RGBColor[Abs[Sin[n]],0,1/n],204060801001.541.561.581.6210203040501.522.533.544.5第121页共29页第120页共29页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第121页共29页Line[{{sn,0},{sn,1}}]}]];n++];Show[g,PlotRange->{-0.2,1.3},Axes->True];则输出所给级数部分和的图形(图1.5),从图中可观察到它收敛于0.693附近的一个数.图1.5例1.3求∑n=1∞14n2+8n+3的值.输入Sum[x^(3k),{k,1,Infinity}]得到和函数−x3−1+x3例1.4(教材例1.3)设an=10nn!,求∑n=1∞an.输入Clear[a];a[n_]=10^n/(n!);vals=Table[a[n],{n,1,25}];ListPlot[vals,PlotStyle->PointSize[0.012]]0.6880.6920.6940.6960.698-0.20.20.40.60.811.2第122页共29页第121页共29页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第122页共29页则输出an的散点图(1.6),从图中可观察an的变化趋势.输入Sum[a[n],{n,l,Infinity}]则输出所求级数的和.图1.6求幂级数的收敛域例1.5(教材例1.4)求∑n=0∞42n(x−3)nn+1的收敛域与和函数.输入Clear[a];a[n_]=4^(2n)*(x-3)^n/(n+1);stepone=a[n+1]/a[n]//Simplify则输出16(1+n)(−3+x)2+n再输入steptwo=Limit[stepone,n->Infinity]则输出5101520255001000150020002500第123页共29页第122页共29页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第123页共29页16(−3+x)这里对a[n+1]和a[n]都没有加绝对值.因此上式的绝对值小于1时,幂级数收敛;大于1时发散.为了求出收敛区间的端点,输入ydd=Solve[steptwo==1,x]zdd=Solve[steptwo==-1,x]则输出{{x→4916}}与{{x→4716}}由此可知,当47164916时,级数发散.为了判断端点的敛散性,输入Simplify[a[n]/.x->(49/16)]则输出右端点处幂级数的一般项为1n+1因此,在端点x=4916处,级数发散.再输入Simplify[a[n]/.x->(47/16)]则输出左端点处幂级数的一般项为(−1)nn+1因此,在端点x=4716处,级数收敛.也可以在收敛域内求得这个级数的和函数.输入Sum[4^(2n)*(x-3)^n/(n+1),{n,0,Infinity}]则输出−Log[1−16(−3+x)]16(−3+x)函数的幂级数展开例1.6(教材例1.5)求cosx的6阶麦克劳林展开式.第124页共29页第123页共29页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第124页共29页输入Series[Cos[x],{x,0,6}]则输出1−x22+x424−x6720+o[x]7注:这是带皮亚诺余项的麦克劳林展开式.例1.6(教材例1.6)求lnx在x=1处的6阶泰勒展开式.输入Series[Log[x],{x,1,6}]则输出(x−1)−(x−1)22+(x−1)33−(x−1)44+(x−1)55−(x−1)66+o[x]7.例1.7(教材例1.7)求arctanx的5阶泰勒展开式.输入serl=Series[ArcTan[x],{x,0,5}];Poly=Normal[serl]则输出arctanx的近似多项式x−x33+x55通过作图把arctanx和它的近似多项式进行比较.输入Plot[Evaluate[{ArcTan[x],Poly}],{x,-3/2,3/2},PlotStyle-...