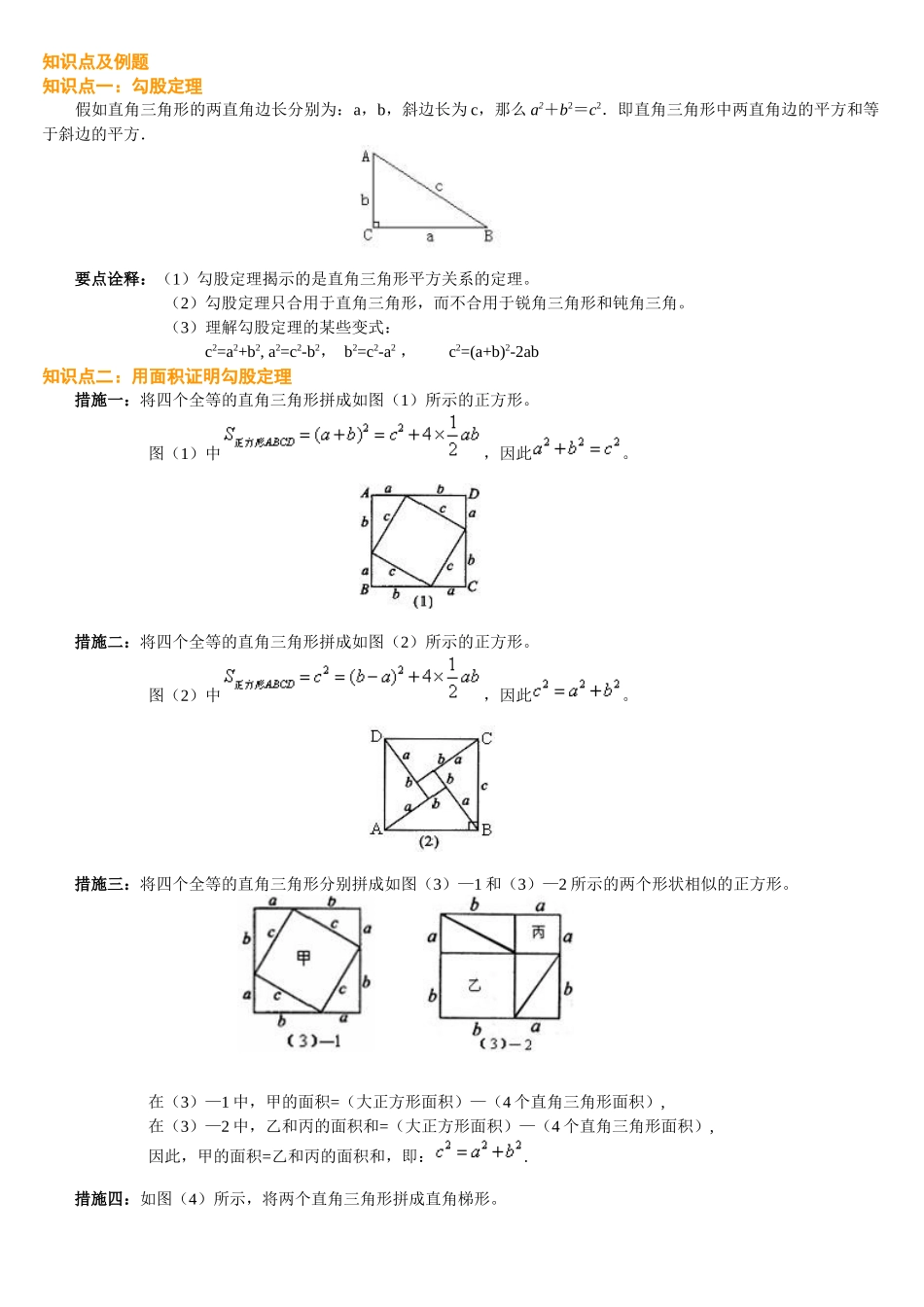
知识点及例题知识点一:勾股定理假如直角三角形的两直角边长分别为:a,b,斜边长为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方.要点诠释:(1)勾股定理揭示的是直角三角形平方关系的定理。(2)勾股定理只合用于直角三角形,而不合用于锐角三角形和钝角三角。(3)理解勾股定理的某些变式:c2=a2+b2,a2=c2-b2,b2=c2-a2,c2=(a+b)2-2ab知识点二:用面积证明勾股定理措施一:将四个全等的直角三角形拼成如图(1)所示的正方形。图(1)中,因此。措施二:将四个全等的直角三角形拼成如图(2)所示的正方形。图(2)中,因此。措施三:将四个全等的直角三角形分别拼成如图(3)—1和(3)—2所示的两个形状相似的正方形。在(3)—1中,甲的面积=(大正方形面积)—(4个直角三角形面积),在(3)—2中,乙和丙的面积和=(大正方形面积)—(4个直角三角形面积),因此,甲的面积=乙和丙的面积和,即:.措施四:如图(4)所示,将两个直角三角形拼成直角梯形。,因此。知识点三:勾股定理的作用1.已知直角三角形的两条边长求第三边;2.已知直角三角形的一条边,求另两边的关系;3.用于证明平方关系的问题;4.运用勾股定理,作出长为的线段。2.在理解的基础上熟悉下列勾股数满足不定方程x2+y2=z2的三个正整数,称为勾股数(又称为高数或毕达哥拉斯数),显然,以x,y,z为三边长的三角形一定是直角三角形。熟悉下列勾股数,对解题是会有协助的:①3、4、55②、12、13;③8、15、17;④7、24、25;⑤10、24、26;⑥9、40、41.假如(a,b,c)是勾股数,当t>0时,以at,bt,ct为三角形的三边长,此三角形必为直角三角形。经典例题透析类型一:勾股定理的直接使用方法1、在RtABC△中,∠C=90°(1)已知a=6,c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a.思绪点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。解析:(1)在△ABC中,∠C=90°,a=6,c=10,b=(2)在△ABC中,∠C=90°,a=40,b=9,c=(3)在△ABC中,∠C=90°,c=25,b=15,a=总结升华:有某些题目的图形较复杂,但中心思想还是化为直角三角形来处理。如:不规则图形的面积,可转化为特殊图形求解,本题通过将图形转化为直角三角形的措施,把四边形面积转化为三角形面积之差或和。举一反三【变式】:如图∠B=∠ACD=90°,AD=13,CD=12,BC=3,则AB的长是多少?【答案】 ∠ACD=90°AD=13,CD=12∴AC2=AD2-CD2=132-122=25∴AC=5又 ∠ABC=90°且BC=3∴由勾股定理可得AB2=AC2-BC2=52-32=16∴AB=4∴AB的长是4.类型二:勾股定理的构造应用2、如图,已知:在中,,,.求:BC的长.思绪点拨:由条件,想到构造含角的直角三角形,为此作于D,则有,,再由勾股定理计算出AD、DC的长,进而求出BC的长.解析:作于D,则因,∴(的两个锐角互余)∴(在中,假如一种锐角等于,那么它所对的直角边等于斜边的二分之一).根据勾股定理,在中,.根据勾股定理,在中,.∴.总结升华:运用勾股定理计算线段的长,是勾股定理的一种重要应用.当题目中没有垂直条件时,也常常作垂线构造直角三角形以便应用勾股定理.举一反三【变式1】如图,已知:,,于P.求证:.思绪点拨:图中已经有两个直角三角形,不过还没有以BP为边的直角三角形.因此,我们考虑构造一种以BP为一边的直角三角形.因此连结BM.这样,实际上就得到了4个直角三角形.那么根据勾股定理,可证明这几条线段的平方之间的关系.解析:连结BM,根据勾股定理,在中,.而在中,则根据勾股定理有.∴又 (已知),∴.在中,根据勾股定理有,∴.【变式2】已知:如图,∠B=D=90°∠,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。分析:怎样构造直角三角形是解本题的关键,可以连结AC,或延长AB、DC交于F,或延长AD、BC交于点E,根据本题给定的角应选后两种,深入根据本题给定的边选第三种较为简朴。解析:延长AD、BC交于E。 ∠A=60°∠,∠B=90°,∴∠E=30°。∴AE=2AB=8,CE=2CD=4,∴BE2=AE2-AB2=82-42=48,BE==。 DE2=CE2-CD2=42-22=12,∴DE==。∴S四边形ABCD=SABE△-SCDE△=AB·BE-CD·DE=类型三:勾股定理的实际应用(一)用勾股定...