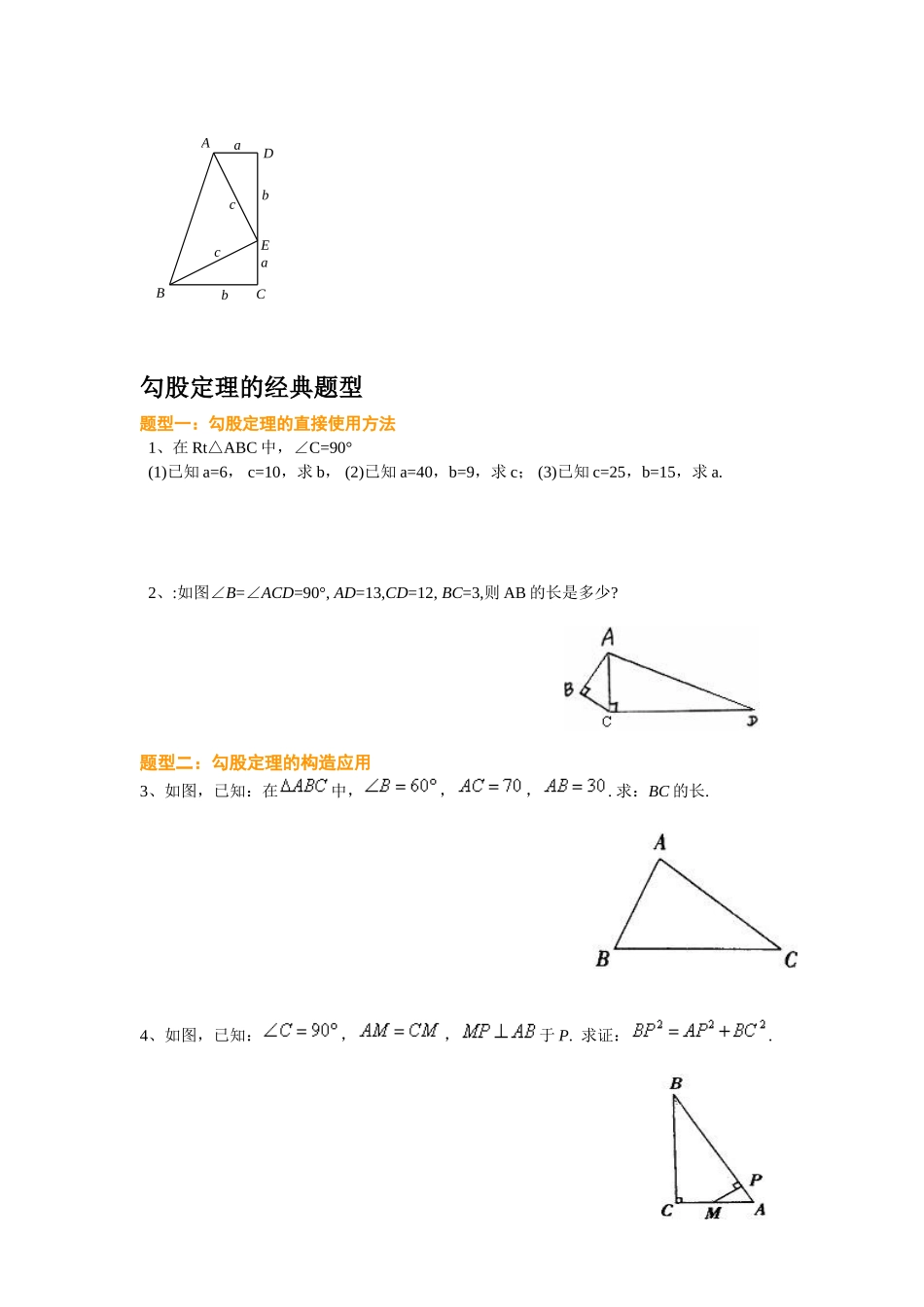
勾股定理知识点一、勾股定理:1、勾股定理定义:假如直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:假如三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。2.勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。)*附:常见勾股数:3,4,5;6,8,10;9,12,15;5,12,133.判断直角三角形:假如三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。(经典直角三角形:勾三、股四、弦五)其他措施:(1)有一种角为90°的三角形是直角三角形。(2)有两个角互余的三角形是直角三角形。用它判断三角形与否为直角三角形的一般环节是:(1)确定最大边(不妨设为c);(2)若c2=a2+b2,则△ABC是以∠C为直角的三角形;若a2+b2<c2,则此三角形为钝角三角形(其中c为最大边);若a2+b2>c2,则此三角形为锐角三角形(其中c为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的二分之一(2)在直角三角形中,假如一种锐角等于30°,那么它所对的直角边等于斜边的二分之一。(3)在直角三角形中,假如一条直角边等于斜边的二分之一,那么这条直角边所对的角等于30°。5.勾股定理的作用:(1)已知直角三角形的两边求第三边。(2)已知直角三角形的一边,求另两边的关系。(3)用于证明线段平方关系的问题。(4)运用勾股定理,作出长为的线段6、勾股定理的证明勾股定理的证明措施诸多,常见的是拼图的措施用拼图的措施验证勾股定理的思绪是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会变化②根据同一种图形的面积不一样的表达措施,列出等式,推导出勾股定理常见措施如下:措施一:,,化简可证.cbaHGFEDCBA措施二:bacbaccabcab四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为大正方形面积为因此措施三:,,化简得证abccbaEDCBA勾股定理的经典题型题型一:勾股定理的直接使用方法1、在Rt△ABC中,∠C=90°(1)已知a=6,c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a.2、:如图∠B=∠ACD=90°,AD=13,CD=12,BC=3,则AB的长是多少?题型二:勾股定理的构造应用3、如图,已知:在中,,,.求:BC的长.4、如图,已知:,,于P.求证:.5、已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。类型三:勾股定理的实际应用(一)用勾股定理求两点之间的距离问题6、如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了抵达B点,然后再沿北偏西30°方向走了500m抵达目的地C点。(1)求A、C两点之间的距离。(2)确定目的地C在营地A的什么方向。7、一辆装满货品的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?(二)用勾股定理求最短问题8、国家电力总企业为了改善农村用电电费过高的现实状况,目前正在全国各地农村进行电网改造,某地有四个村庄A、B、C、D,且恰好位于一种正方形的四个顶点,现计划在四个村庄联合架设一条线路,他们设计了四种架设方案,如图实线部分.请你协助计算一下,哪种架设方案最省电线.9、如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短旅程.类型四:运用勾股定理作长为的线段10、作长为、、的线段。11、假如ΔABC的三边分别为a、b、c,且满足a2+b2+c2+50=6a+8b+10c,判断ΔABC的形状。12、四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积。13、已知:△ABC的三边分别为m2-n2,2mn,m2+n2(m,n为正整数,且m>n),判断△ABC与否为直角三角形.14、如图正方形ABCD,E为BC中点,F为AB上一点,且BF=AB。请问FE与DE与否垂直?请阐明。15、若直角三角形两直角边的比是3:4,斜边长是20,求此直角三角形的面积。16、等边三角形的边长为2,求它的面...