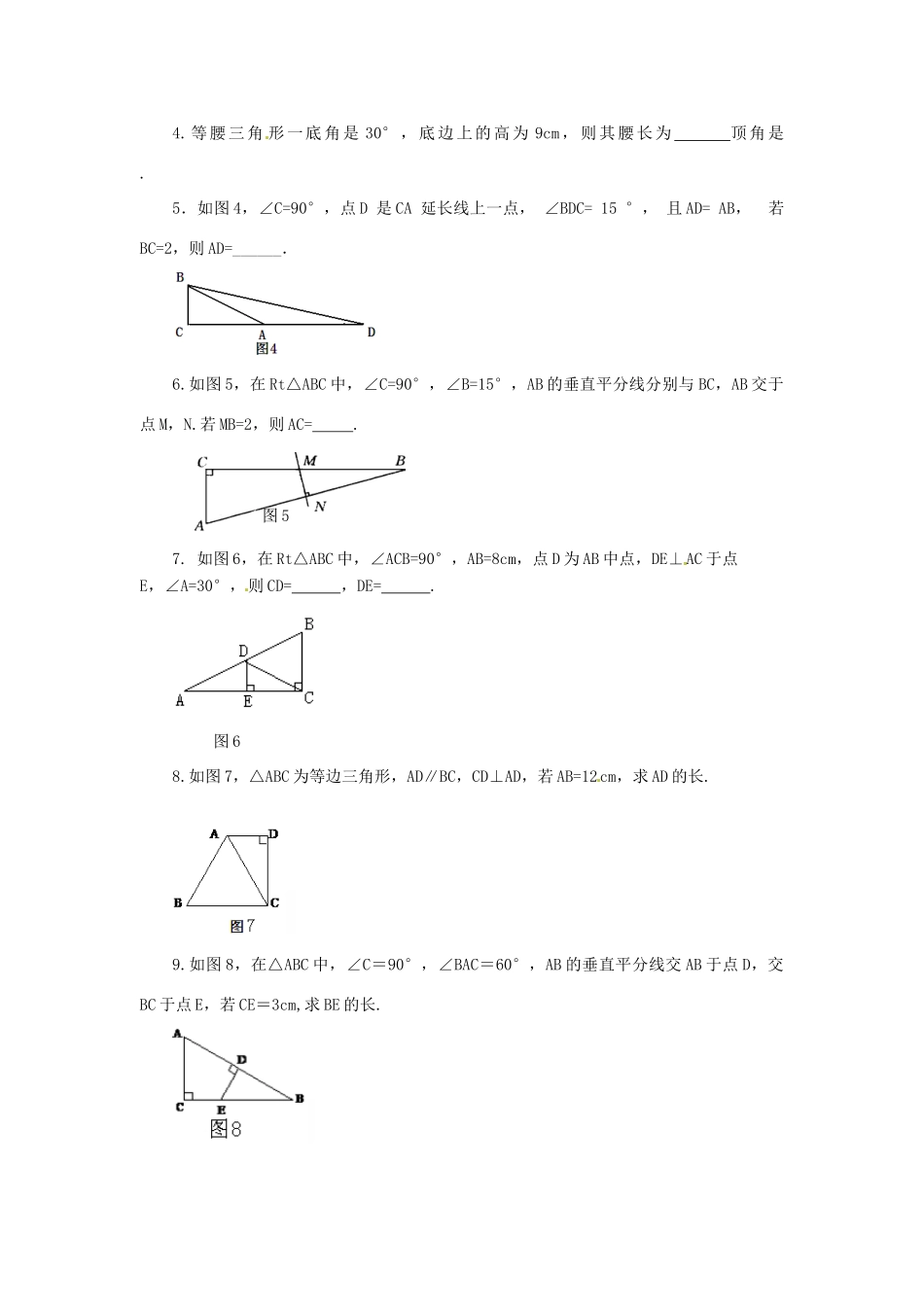
17.2直角三角形一、课前小测1.如图1,在等边三角形ABC中,AD⊥BC,则∠BAD=°,BD=AB.2.在Rt△ABC中,∠C=90°,∠A=30°.(1)若测得AB=5cm,BC=2.5cm,则AB=BC;(2)若测得AB=10cm,BC=5cm,则AB=BC;(3)若AB=a,则BC=.由此你发现了什么结论?二、典型问题【问题1】如图2,在△ABC中,∠ACB=90°,CD是高,∠A=30°.试猜想BD与AB的关系,并证明你的猜想.【问题2】如图3,在△ABC中,∠ACB=90°,CD,CE三等分∠ACB,CD⊥AB,求证:(1)AB=2BC;(2)CE=AE=EB.三、技能训练3.在Rt△ABC中,∠C=90°,∠A=60°,若AB=4cm,则AC=.4.等腰三角形一底角是30°,底边上的高为9cm,则其腰长为顶角是.5.如图4,∠C=90°,点D是CA延长线上一点,∠BDC=15°,且AD=AB,若BC=2,则AD=______.6.如图5,在Rt△ABC中,∠C=90°,∠B=15°,AB的垂直平分线分别与BC,AB交于点M,N.若MB=2,则AC=.图57.如图6,在Rt△ABC中,∠ACB=90°,AB=8cm,点D为AB中点,DE⊥AC于点E,∠A=30°,则CD=,DE=.图68.如图7,△ABC为等边三角形,AD∥BC,CD⊥AD,若AB=12cm,求AD的长.9.如图8,在△ABC中,∠C=90°,∠BAC=60°,AB的垂直平分线交AB于点D,交BC于点E,若CE=3cm,求BE的长.四、拓展应用10.如图9,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,你能否根据现有条件求出PD的长.五、知识梳理★在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的.★注意:该定理的使用条件必须是在直角三角形中,否则在一般的三角形中不存在这一定理.六、本课作业11.如图10,在中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD=.12.如图11,已知∠MAN,AC平分∠MAN,,若∠MAN=120°,∠ABC=∠ADC=90°,求证:AB+AD=AC.