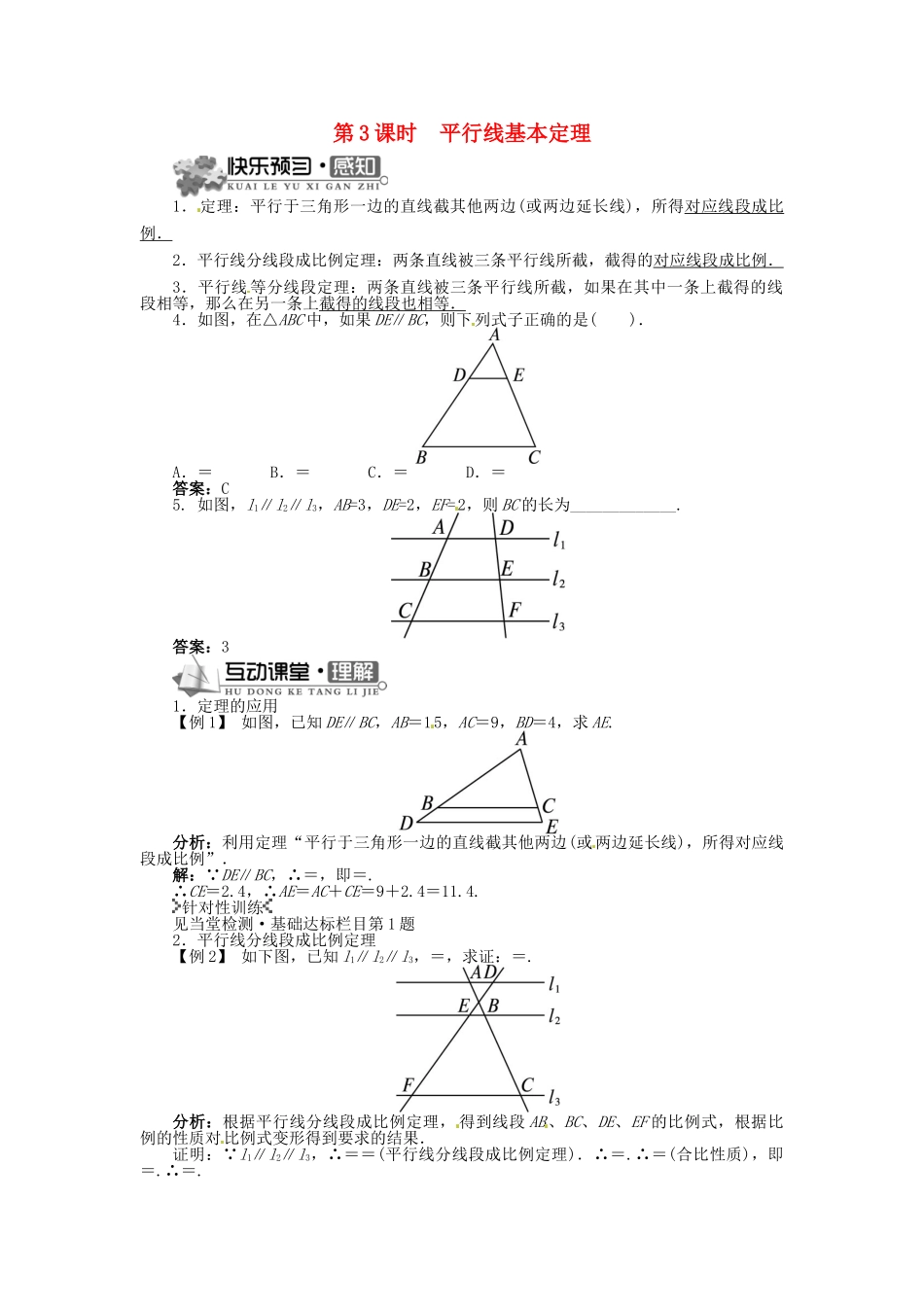
第3课时平行线基本定理1.定理:平行于三角形一边的直线截其他两边(或两边延长线),所得对应线段成比例.2.平行线分线段成比例定理:两条直线被三条平行线所截,截得的对应线段成比例.3.平行线等分线段定理:两条直线被三条平行线所截,如果在其中一条上截得的线段相等,那么在另一条上截得的线段也相等.4.如图,在△ABC中,如果DE∥BC,则下列式子正确的是().A.=B.=C.=D.=答案:C5.如图,l1∥l2∥l3,AB=3,DE=2,EF=2,则BC的长为_____________.答案:31.定理的应用【例1】如图,已知DE∥BC,AB=15,AC=9,BD=4,求AE.分析:利用定理“平行于三角形一边的直线截其他两边(或两边延长线),所得对应线段成比例”.解:∵DE∥BC,∴=,即=.∴CE=2.4,∴AE=AC+CE=9+2.4=11.4.针对性训练见当堂检测·基础达标栏目第1题2.平行线分线段成比例定理【例2】如下图,已知l1∥l2∥l3,=,求证:=.分析:根据平行线分线段成比例定理,得到线段AB、BC、DE、EF的比例式,根据比例的性质对比例式变形得到要求的结果.证明:∵l1∥l2∥l3,∴==(平行线分线段成比例定理).∴=.∴=(合比性质),即=.∴=.针对性训练见当堂检测·基础达标栏目第3题1.如图,△ABC中,DE∥BC,AD=1,DB=2,AE=2,那么EC等于().A.1B.2C.3D.4解析:∵DE∥BC,∴=,即=.∴EC=4.答案:D2.如图,已知直线a∥b∥c,直线m、n与a、b、c分别交于点A、C、E、B、D、F,AC=4,CE=6,BD=3,则BF=().A.7B.7.5C.8D.8.5答案:B3.如图,已知AB∥CD∥EF,那么下列结论正确的是().A.=B.=C.=D.=答案:A4.如图所示,AB⊥BD,CD⊥BD,连接AC交BD于O.若AB=3,BO=4,BD=12,则OC的长是().A.10B.8C.6D.5解析:由已知可知,AB∥CD,AO=5,∴=,∴AC=15.又∵AO=5,∴OC=AC-AO=10.答案:A5.已知四边形ABCD为平行四边形,F在BC上,E在DC上,且AF∶FE=2∶3.求:(1)CF∶BF;(2)BF∶AD;(3)CE∶ED.解:(1)∵DE∥AB,∴==.(2)∵DE∥AB,∴==.∵BC=AD,∴=.(3)∵BC∥AD,∴==.