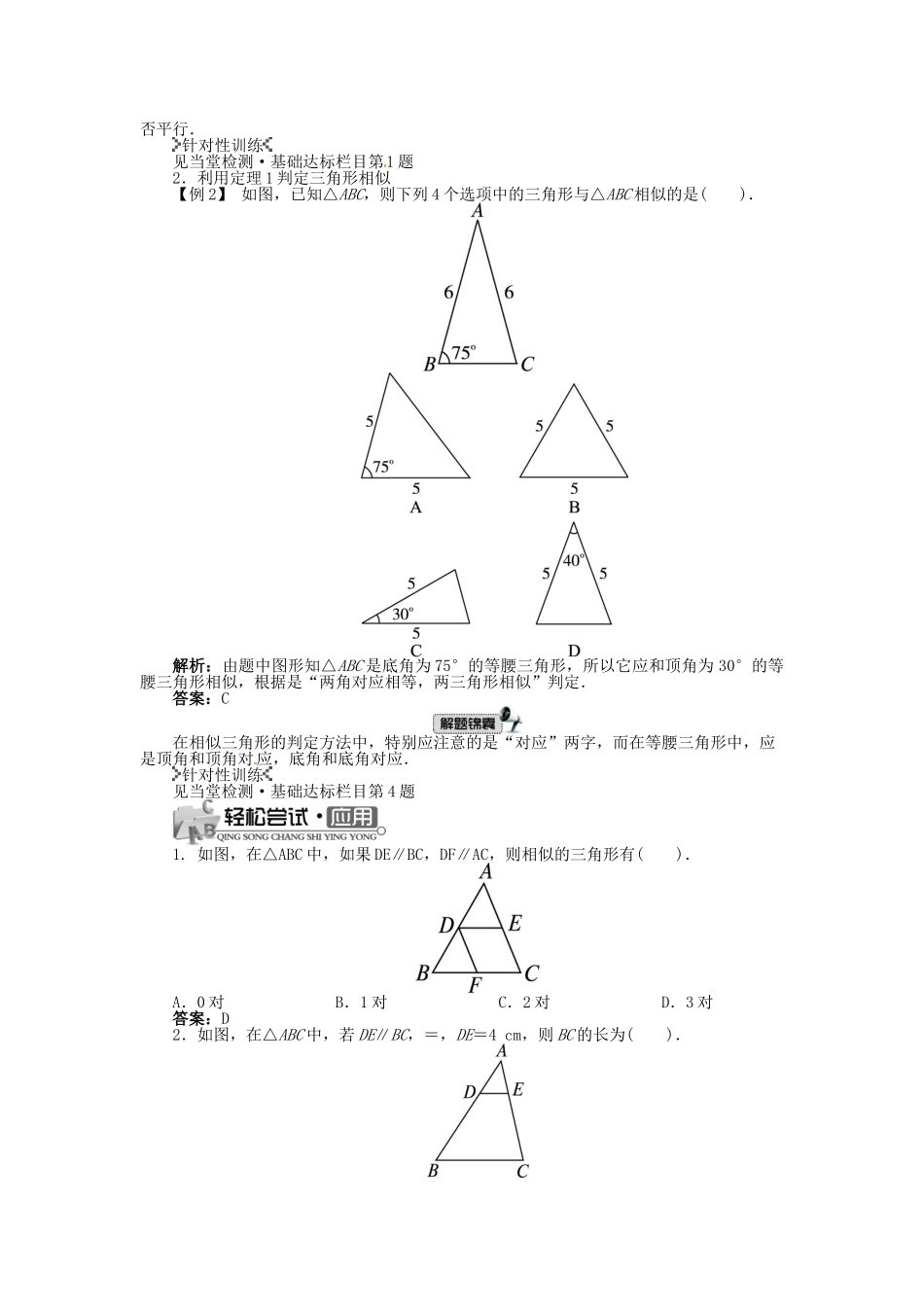
相似三角形的判定第1课时相似三角形的判定定理11.△ABC∽△A′B′C′,相似比为k1,△A′B′C′∽△ABC,相似比为k2,则k1k2=1.三角形全等是三角形相似的特例.2.定理:平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.3.定理1:如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似(可简单说成:两角对应相等的两个三角形相似).4.如图,在△ABC中,D、E分别是AB、AC边的中点,若BC=6,则DE等于().A.5B.4C.3D.2答案:C5.如图,Rt△ABC中,∠C=90°,DE⊥AB于E,试说明△ABC和△ADE的关系?解:△ABC和△ADE相似.∵∠A=∠A,∠C=∠AED=90°,∴△ABC∽△ADE.1.利用定理:“平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似”判定三角形相似【例1】如图,在△ABC中,D、E分别是AB、AC上的点,且AD=AB,AE=EC.求证:△ADE∽△ABC.分析:根据条件证明DE∥BC即可.证明:∵AE=EC,∴=.又∵AD=AB,即=,∴=.∴DE∥BC.∴△ADE∽△ABC.当一个三角形在另一个三角形的内部并且有一个公共角时,通常要看公共角的对边是否平行.针对性训练见当堂检测·基础达标栏目第1题2.利用定理1判定三角形相似【例2】如图,已知△ABC,则下列4个选项中的三角形与△ABC相似的是().解析:由题中图形知△ABC是底角为75°的等腰三角形,所以它应和顶角为30°的等腰三角形相似,根据是“两角对应相等,两三角形相似”判定.答案:C在相似三角形的判定方法中,特别应注意的是“对应”两字,而在等腰三角形中,应是顶角和顶角对应,底角和底角对应.针对性训练见当堂检测·基础达标栏目第4题1.如图,在△ABC中,如果DE∥BC,DF∥AC,则相似的三角形有().A.0对B.1对C.2对D.3对答案:D2.如图,在△ABC中,若DE∥BC,=,DE=4cm,则BC的长为().A.8cmB.12cmC.11cmD.10cm解析:∵DE∥BC,∴△ADE∽△ABC.∴=.又∵=,∴=.∴=.∴BC=3DE=12cm.答案:B3.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为().A.B.C.D.2解析:∵DE垂直平分AB,∴BD=AB=2.5.∵∠B=∠B,∠BCA=∠BDE=90°,∴△BCA∽△BDE.∴=.∴=.∴BE=.∴CE=BE-BC=-3=.答案:B4.已知△ABC和△DEF中,点A、B、C分别与点D、E、F相对应,且∠A=70°,∠B=34°,∠D=70°,则当∠F=__________时,△ABC∽△DEF.解析:由已知可知∠A和∠D对应,∠B和∠E对应,∠C和∠F对应,所以∠F=∠C=180°-∠A-∠B=76°.答案:76°5.如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果=,那么=__________.解析:平行四边形ABCD中,∵=,又∵AD=BC,∴=.∵AD∥BC,∴=.∴=.答案: