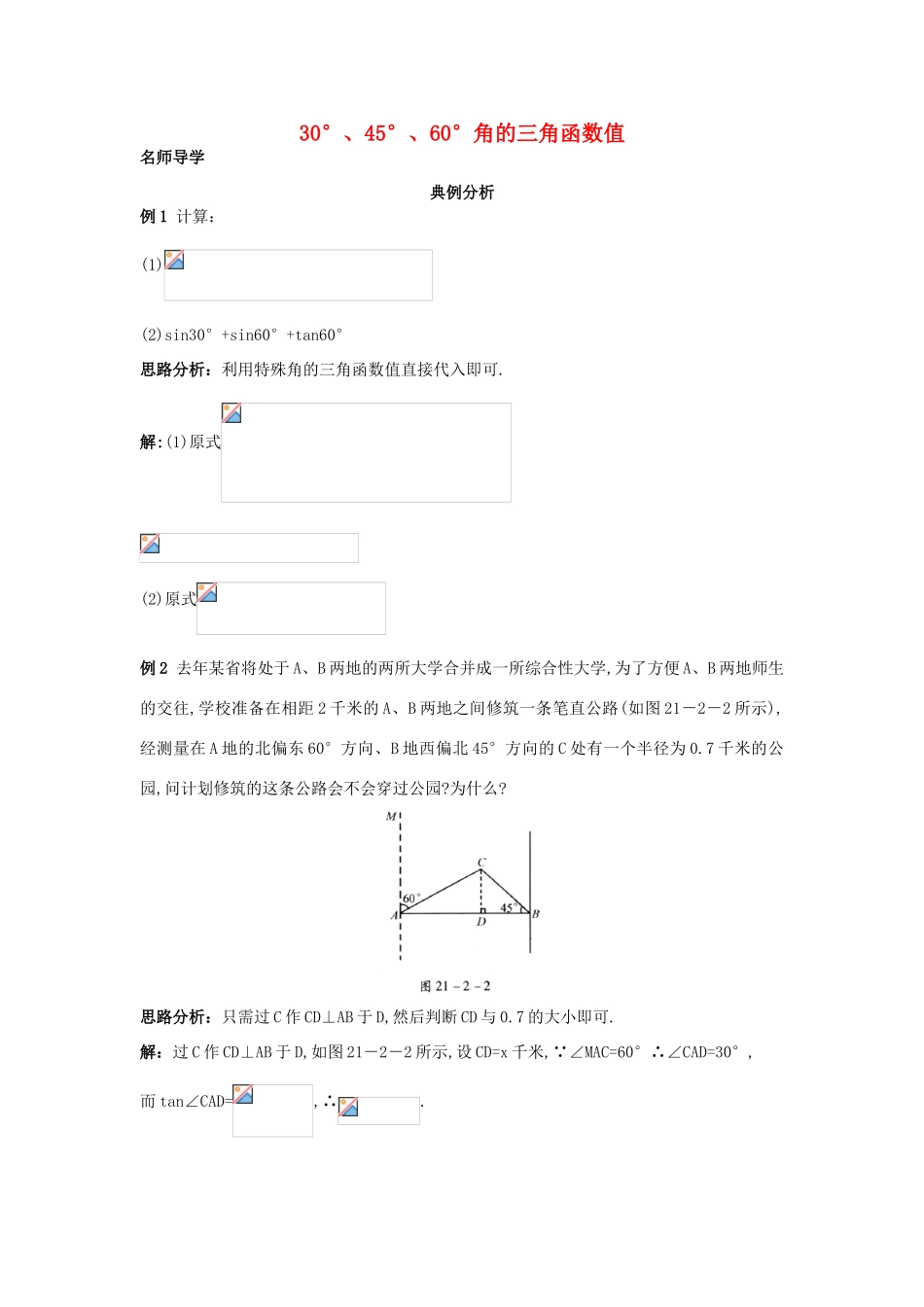
30°、45°、60°角的三角函数值名师导学典例分析例1计算:(1)(2)sin30°+sin60°+tan60°思路分析:利用特殊角的三角函数值直接代入即可.解:(1)原式(2)原式例2去年某省将处于A、B两地的两所大学合并成一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2千米的A、B两地之间修筑一条笔直公路(如图21-2-2所示),经测量在A地的北偏东60°方向、B地西偏北45°方向的C处有一个半径为0.7千米的公园,问计划修筑的这条公路会不会穿过公园?为什么?思路分析:只需过C作CD⊥AB于D,然后判断CD与0.7的大小即可.解:过C作CD⊥AB于D,如图21-2-2所示,设CD=x千米,∵∠MAC=60°∴∠CAD=30°,而tan∠CAD=,∴.又∠ABC=45°,∴tan∠ABC==1,∴BD=x.又∵AB=2=AD+DB=,∴≈0.732>0.7.即计划修筑的这条公路不会穿过公园.突破易错☆挑战零失误规律总结善于总结★触类旁通1方法点拨:一般情况下求这类式子的值,先要将各角的三角函数值代入,然后化简.因此,需要熟记特殊角的三角函数值,需注意的是,这类题虽然简单,但很容易出错,因而要特别注意.2方法点拨:此类题一般都可转化为直角三角形的问题来解决,其中特殊角的三角函数值为解决此问题提供了有力的保障,应注意从中积累经验.