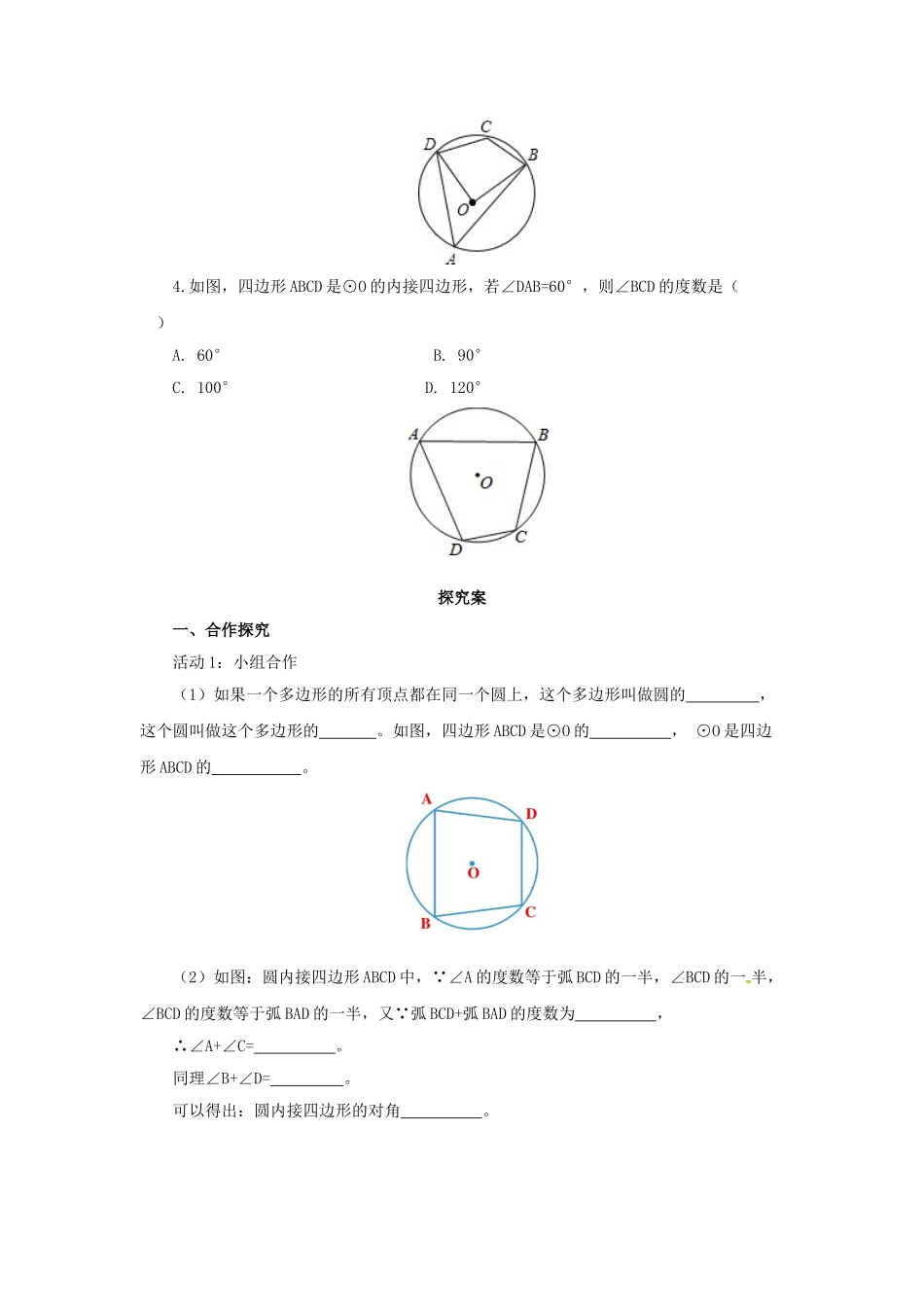
21.4.2圆周角预习案一、预习目标及范围:1.通过学习,理解圆内接四边形的性质。(难点)2.能够掌握圆内接四边形的概念。(重点)3.运用所学的知识解决实际的问题。二、预习要点1.什么是圆内接四边形?2.圆内接四边形的性质是什么?三、预习检测1.如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是()A.100°B.110°C.120°D.130°2.如图,四边形ABCD是⊙O的内接四边形,∠B=70°,则∠D的度数是()A.110°B.90°C.70°D.60°3.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是()A.88°B.92°C.106°D.136°4.如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是()A.60°B.90°C.100°D.120°探究案一、合作探究活动1:小组合作(1)如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆的,这个圆叫做这个多边形的。如图,四边形ABCD是⊙O的,⊙O是四边形ABCD的。(2)如图:圆内接四边形ABCD中,∵∠A的度数等于弧BCD的一半,∠BCD的一半,∠BCD的度数等于弧BAD的一半,又∵弧BCD+弧BAD的度数为,∴∠A+∠C=。同理∠B+∠D=。可以得出:圆内接四边形的对角。如图:如果延长BC到E,那么∠DCE+∠BCD=,又∵∠A+∠BCD=,∴∠A=,可以得出:圆内接四边形的任意一个外角等于它的。活动内容2:典例精析例题1、已知:在⊙O中,直径AB的长为10cm,弦AC的长为6cm,∠ACB的平分线交⊙O于点D,求BC,AD和BD的长。分析:∵AB为直径,∴∠ACB=∠ADB=90°。在Rt△ACB中,BC=AB2-AC2=102-62=8(cm)∵CD平分∠ACB,∴弧AD=弧BD。∴AD=BD。在等腰直角三角形ADB中,AD=BD=ABsin45°=10(2/2)=52(cm)∴BC=8cm,AD=BD=52cm。二、随堂检测1.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是()A.115°B.105°C.100°D.95°2.如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若∠ADB=100°,则∠ACB的度数为()A.35°B.40°C.50°D.80°3.如图,四边形ABCD内接于⊙O,若∠C=36°,则∠A的度数为()A.36°B.56°C.72°D.144°4.如图,四边形ABCD为⊙O的内接四边形,若∠BCD=110°,则∠BAD为()A.140°B.110°C.90°D.70°5.如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD()A.128°B.100°C.64°D.32°6.圆内接四边形ABCD中,若∠A:∠B:∠C=1:2:5,则∠D等于。7.圆内接四边形ABCD中,∠A,∠B,∠C的度数的比为2:3:6,∠D的度数为。8.已知四边形ABCD内接于圆,∠A=2∠C,则∠C等于()A.90°B.60°C.45°D.30°参考答案预习检测:1.B2.A3.D4.D随堂检测1.B2.B3.D4.D5.A6.120°7.112.5°8.B