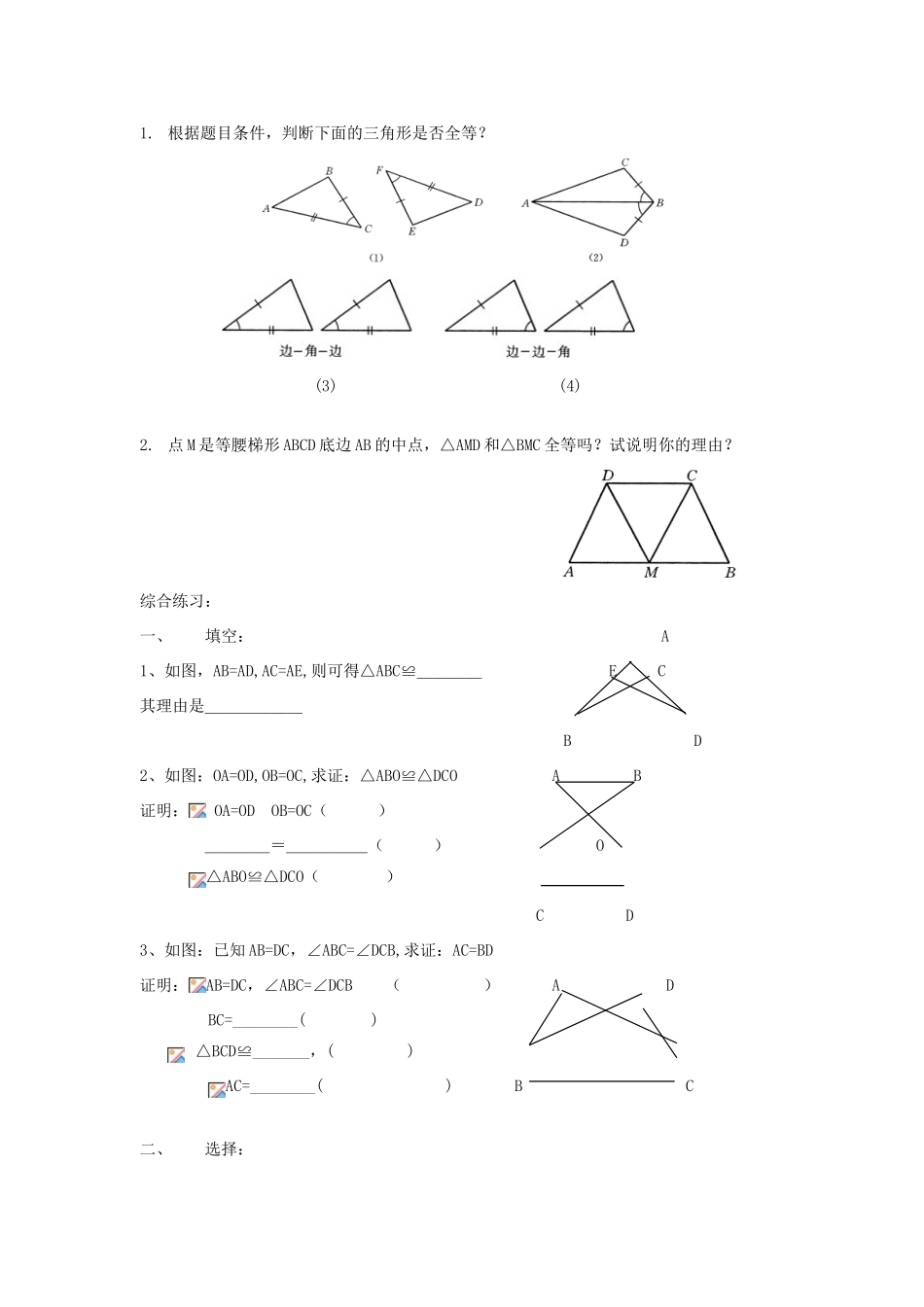
19.2.2全等三角形的识别(二)(SAS)学习目标:会运用“边角边”公理证明三角形全等的简单问题重点与难点:1、会运用“边角边”公理证明三角形全等的简单问题2、分清用两边一角证明三角形相似和全等的不同。教学过程:知识回顾:一、判别三角形相似的方法之二:1、如果两个三角形有_____边对应______,并且____相等,那么这两个三角形相似.新课讲解:做一做以图24.2.5中的两条线段和一个角画一个三角形,使该角恰为这两条线段的夹角.步骤:1、画一线段AB使它的长度等于4cm.2、以点A为顶点,作∠BAP=45°,在射线AP上截取AC=3cm,3、连结BC.△ABC即为所求.把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗?换两条线段和一个角,用同样的方法试试,是否有同样的结论.ACABA这样我们就得到识别三角形全等的另一种简便的方法如果两个三角形有_____边及其______分别对应____,那么这两个三角形全等.简记为(S.A.S.).对比判别三角形相似的方法如果两个三角形有_____边对应______,并且____相等,那么这两个三角形相似.例2如图24.2.6,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD.解AD平分∠BACA∠_____=∠_____,又AB=AC,AD为__________,△ABD≌△ACD.()BDC做一做如图24.2.7,已知两条线段和一个角,以这两条线段为边,以这个角为其中一条边的对角,画一个三角形.图24.2.7把你画的三角形与其他同学画的三角形进行比较,所有的三角形一定都会全等吗?练习1.根据题目条件,判断下面的三角形是否全等?(3)(4)2.点M是等腰梯形ABCD底边AB的中点,△AMD和△BMC全等吗?试说明你的理由?综合练习:一、填空:A1、如图,AB=AD,AC=AE,则可得△ABC≌____EC其理由是______BD2、如图:OA=OD,OB=OC,求证:△ABO≌△DCOAB证明:OA=ODOB=OC()____=_____()O△ABO≌△DCO()CD3、如图:已知AB=DC,∠ABC=∠DCB,求证:AC=BD证明:AB=DC,∠ABC=∠DCB()ADBC=________()△BCD≌_______,()AC=________()BC二、选择:1、在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么△ABC中与这个角对应的角是()A∠AB∠BC∠CD∠B或∠Dl2、如图:直线l是四边形ABCD的对称轴,如果,有下列A结论:(1)AB∥DC(2)AB=BC(3)ABBC(4)AO=OC,BOD其中正确的结论有()A1个B2个C3个D4个C3、具有下列条件的两个等腰三角形,不能判定它们全等的是()A顶角、一腰对应相等B底边、一腰对就相等C两腰对应相等D一腰、一底角、一底边对应相等4、△ABC和△A′B′C′边角条件如图:那么这两个三角形()CC′A全等B不全等C不一定全等D相似2130°130°2A3BA3B′三、证明:1、如图,已知∠1=∠2,AO=BO,那么△AOP≌△BOP,为什么?(第1题)2、已知:AD=BC,∠ADC=∠BCD.求证:∠BDC=∠ACD.(第2题)3、如图,AE=DB,BC=EF,BC∥EF,说明△ABC和△DEF全等的理由.(第3题)4、如图:点M是等腰梯形ABCD底边AB上的中点,则MD与MC的大小有何关系,试说明理由。DCAMB5、已知点A、B、C、D在同一条直线上,AB=CD,∠D=∠ECA,试问:AE与BF的大小关系,并说明理由。EFABCD6、如图:在△ABC中,AB=AC,∠BAC=90°,在AB上取点P,边CA的延长线上取点Q,使AP=AQ,边CP与BQ交于点S,求证:△CAP≌△BAQQSAPBC7、如图,AB=AD,AC=AE,∠BAE=∠DAC,△ABC与△ADE全等吗?并说明理由。全品中考网