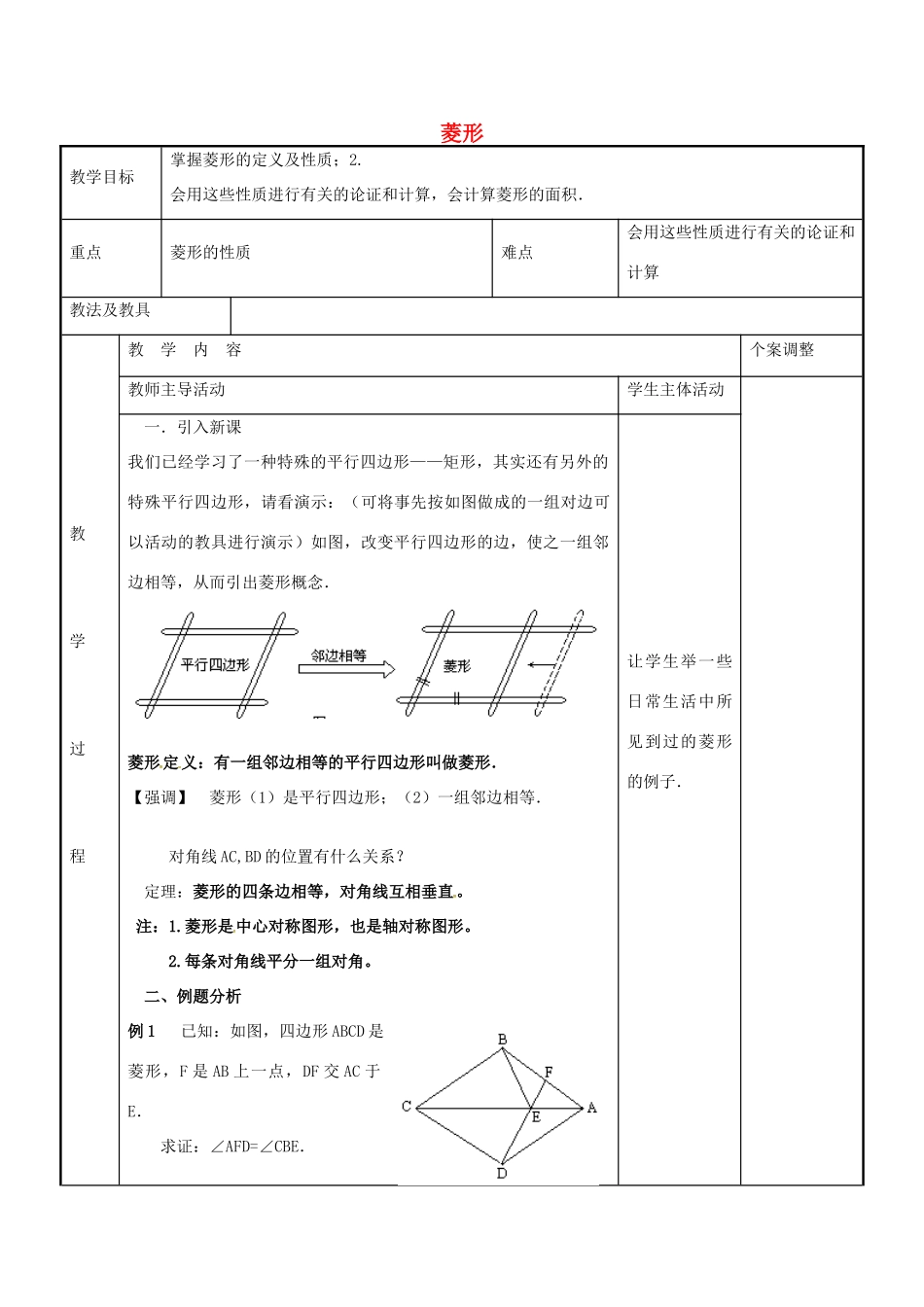
菱形教学目标掌握菱形的定义及性质;2.会用这些性质进行有关的论证和计算,会计算菱形的面积.重点菱形的性质难点会用这些性质进行有关的论证和计算教法及教具教学过程教学内容个案调整教师主导活动学生主体活动一.引入新课我们已经学习了一种特殊的平行四边形——矩形,其实还有另外的特殊平行四边形,请看演示:(可将事先按如图做成的一组对边可以活动的教具进行演示)如图,改变平行四边形的边,使之一组邻边相等,从而引出菱形概念.菱形定义:有一组邻边相等的平行四边形叫做菱形.【强调】菱形(1)是平行四边形;(2)一组邻边相等.对角线AC,BD的位置有什么关系?定理:菱形的四条边相等,对角线互相垂直。注:1.菱形是中心对称图形,也是轴对称图形。2.每条对角线平分一组对角。二、例题分析例1已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.求证:∠AFD=∠CBE.让学生举一些日常生活中所见到过的菱形的例子.教学过程教学内容个案调整教师主导活动学生主体活动证明:∵四边形ABCD是菱形,∴CB=CD,CA平分∠BCD.∴∠BCE=∠DCE.又CE=CE,∴△BCE≌△COB(SAS).∴∠CBE=∠CDE.∵在菱形ABCD中,AB∥CD,∴∠AFD=∠FDC∴∠AFD=∠CBE.例2.四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm,求(1)对角线AC的长度;(2)菱形ABCD的面积.三、随堂练习1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为.2.已知菱形的两条对角线分别是6cm和8cm,求菱形的周长和面积.3.已知菱形ABCD的周长为20cm,且相邻两内角之比是1∶2,求菱形的对角线的长和面积.4.已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.四.小结板书设计(用案人完成)当堂作业教学札记