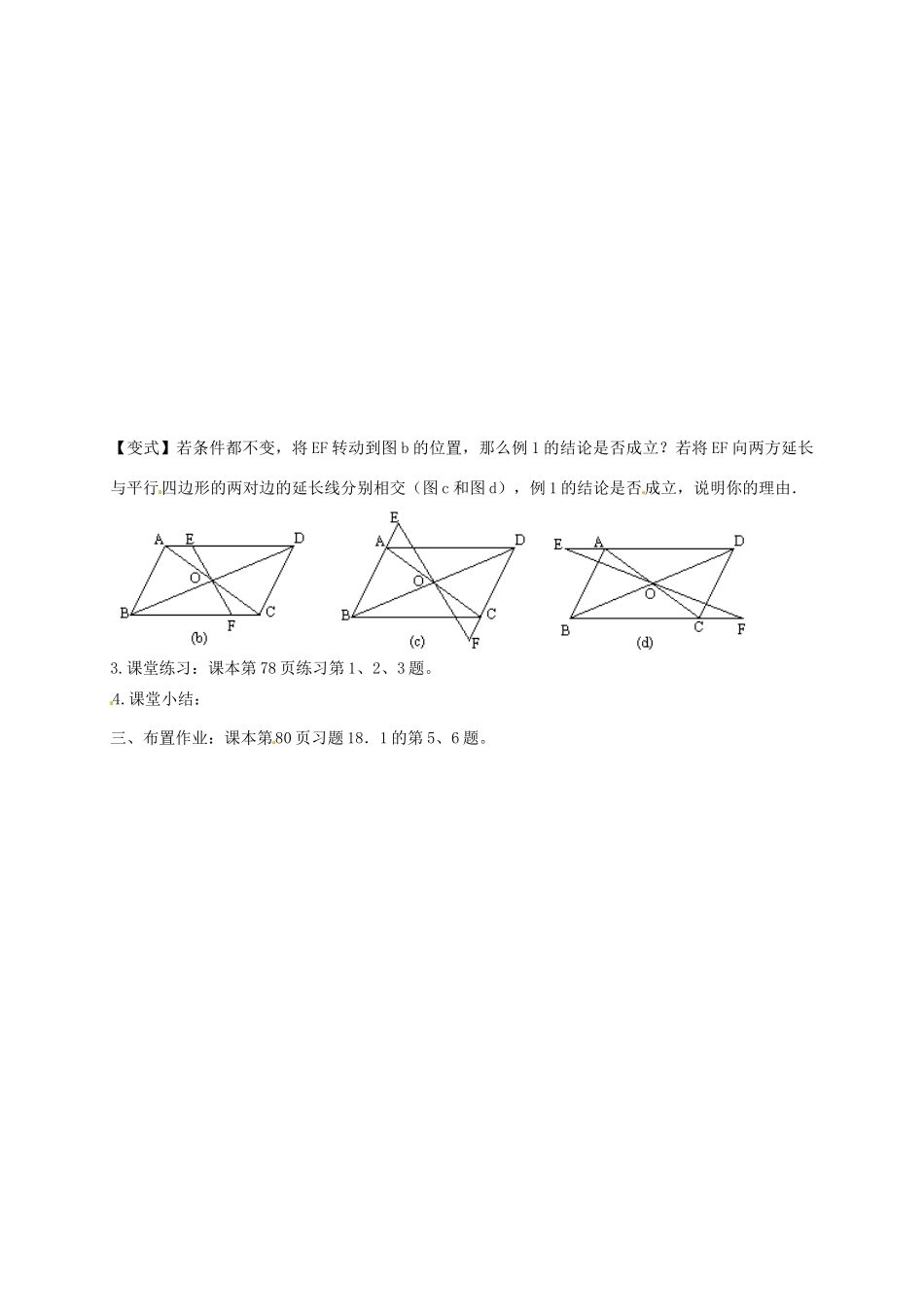
平行四边形第3课时教学内容:平行四边形的性质(3)教学目标:1.理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质。2.能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题。3.培养学生的推理论证能力和逻辑思维能力。教学重点:平行四边形对角线互相平分的性质,以及性质的应用。教学难点:综合运用平行四边形的性质进行有关的证明和计算。教学用具:直尺、三角板。教学过程:一、复习提问:1.什么是平行四边形?四边形与平行四边形的关系是什么?2.前边两节课我们学了哪些性质定理?①平行四边形是中心对称图形.②平行四边形的性质定理1:平行四边形的对边相等.③平行四边形的性质定理2:平行四边形的对角相等.④平行线之间的距离处处相等.3.平行四边形是中心对称图形,那么两条对角线的交点是什么?对角线互相平分吗?二、进行新课:1.平行四边形的性质定理3的证明:平行四边形的性质定理3:平行四边形的对角线互相平分.这里:提问学生口述已知、求证并口述证明过程,然后教师加以讲评及纠正。2.例题讲解:例5.()如图,□ABCD的对角线AC和BD相交于O,△AOB的周长为15,AB=6,那么对角线AC与BD的和是多少?例6.()如图,在□ABCD的对角线AC与BD相交于点O,EF过点O与边AB、CD分别相交于点E、F.求证:OE=OF,AE=CF,BE=DFABCDOCABDEFO【变式】若条件都不变,将EF转动到图b的位置,那么例1的结论是否成立?若将EF向两方延长与平行四边形的两对边的延长线分别相交(图c和图d),例1的结论是否成立,说明你的理由.3.课堂练习:课本第78页练习第1、2、3题。4.课堂小结:三、布置作业:课本第80页习题18.1的第5、6题。