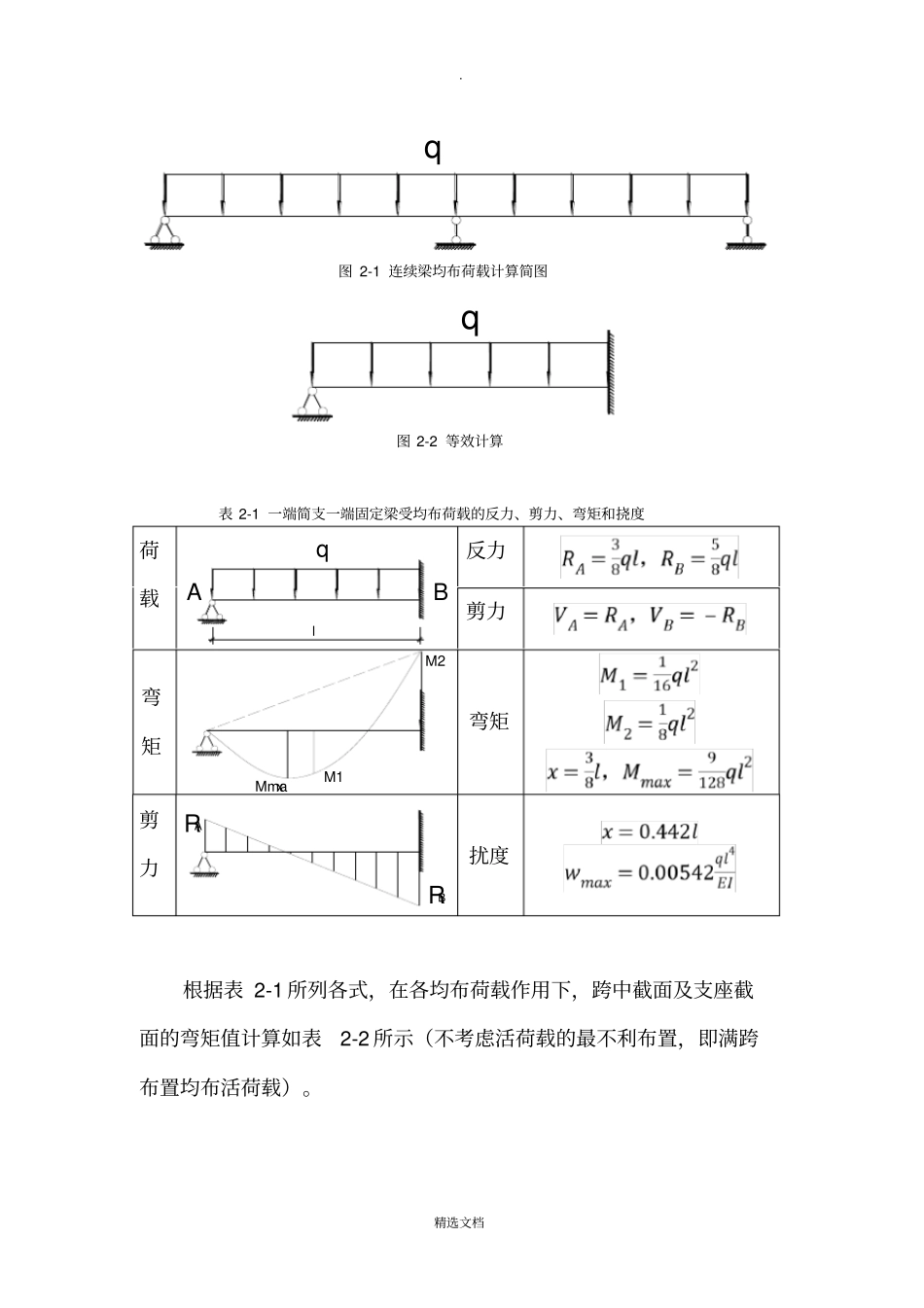
.精选文档东南大学土木工程结构设计作业如图所示,预应力混凝土两跨连续梁,截面尺寸b×h=350mm×900mm,预应力筋线性布置如图所示(二次抛物线),且已知有效预应力为1200kN(沿全长)。(9根直径为15.2mm低松弛1860级钢绞线)混凝土的弹性模量为MPaEc4103.25,(C40混凝土),抗拉强度MPaftk3。(1)若作用60mkN/向下均布荷载(含自重),试计算此时跨中挠度;(2)若均布荷载增加到120mkN/(含自重),此时跨中挠度是否为60mkN/均布荷载下跨中挠度的两倍?如恒载与可变荷载各为60mkN/,梁跨中需要配HRB400钢筋的面积为多少?单位:mm10010010010000100001.预应力梁等效荷载法由题意,预应力钢筋的轴线为二次抛物线,则有效预加力NPe产生一个与均布荷载作用下梁的弯矩图相似的弯矩图。预应力筋的轴线为单波抛物线,则有效预加力NPe在单波抛物线内的梁中将产生一个等效的均布荷载qe,其值:.精选文档(1-1)epn为该抛物线的垂度,即单波抛物线中点到两端点所连成直线的距离,即:(1-2)l为该抛物线在水平线上的投影长度。对称结构选取单跨梁进行分析,其中,,,,,,代入式(1-1)和式(1-2),得:,。作用在双跨连续梁上的等效均布荷载如图1-1所示。qp=50.4KN/m图1-1:双跨连续梁等效均布荷载图2.连续梁弯矩等效荷载qe及恒活荷载q均为作用在双跨连续梁上的均布荷载,计算简图如图2-1所示,根据结构力学相关知识,对称双跨梁在对称荷载作用下,可以等效为一半结构进行分析,约束可以简化为一端简支、一端固定,如图2-2所示,其弯矩、剪力、支座反力及挠度如下表2-1所列。.精选文档q图2-1连续梁均布荷载计算简图q图2-2等效计算表2-1一端简支一端固定梁受均布荷载的反力、剪力、弯矩和挠度荷载qABl反力剪力弯矩M2M1Mmax弯矩剪力RARB扰度根据表2-1所列各式,在各均布荷载作用下,跨中截面及支座截面的弯矩值计算如表2-2所示(不考虑活荷载的最不利布置,即满跨布置均布活荷载)。.精选文档表2-2各均布荷载下跨中截面及支座截面弯矩值(kN·m)荷载(kN/m)M1,kM2,kMmax,k1315630354.3752375750421.87537501500843.754375750421.8755375750421.875对于使用等效荷载法分析后后张法预应力混凝土超静定梁,其综合弯矩可以分为主弯矩和次弯矩两部分,其中,主弯矩为预加力值与偏心距的乘积,次弯矩为综合弯矩减去主弯矩(也可理解为由等效荷载作用下,中间支座反力所产生的附加弯矩)。预应力筋等效弯矩法的综合弯矩图、主弯矩图、次弯矩图如图2-3至2-5所示。630315315354.4354.4图2-3预应力等效荷载的综合弯矩图(kN·m)420420420.精选文档图2-3预应力等效荷载的主弯矩图(kN·m)210105105图2-4预应力等效荷载的主弯矩图(kN·m)3.裂缝控制验算对于裂缝控制验算,应取支座及跨中最不利截面进行验算。由于跨内最不利截面的位置及弯矩与多种因素有关,一般情况下,可取跨中截面和荷载作用下的最大弯矩截面进行验算,即对支座截面和跨中弯矩最大截面验算。3.1.计算截面特征矩形截面梁的截面几何性质如表3-1所列(不考虑后张法预应力孔道对截面积及截面惯性矩的影响)。表3-1矩形截面梁的截面几何性质3.2.验算裂缝控制等级对于问题(1)、(2),可定义三种不同的荷载组合分别计算,荷载组合如表3-2所示。.精选文档表3-2荷载组合荷载组合荷载工况组合1组合2组合33.2.1.按荷载效应的标准组合对于预应力混凝土梁,荷载效应的标准组合下抗裂验算边缘的混凝土法向应力及扣除全部预应力损失后在抗裂度验算边缘的混凝土预压应力计算公式如式(3-1)及式(3-2)所示(考虑到截面积相对于预应力孔道面积及预应力筋的面积大的多,实际计算时用I、A代替I0、In、An计算)。(1)中间支座截面:(3-1)(2)跨中截面:(3-2)梁的标准组合弯矩值为:,按荷载效应的标准.精选文档组合时的抗裂等级验算如表3-2所示。表3-2荷载效应标准组合抗裂等级验算组合截面(kNm)(MPa)(MPa)(MPa)组合1支座75015.8717.14-1.27<0,一级跨中421.888.9311.31-2.38<0,一级组合2支座150031.7417.1414.6>ftk=3.0,三级跨中843.7517.8611.316.55>ftk=3.0,三级组合3支座150031.7417.1414.6>ftk=3.0,三级跨中843.7517....