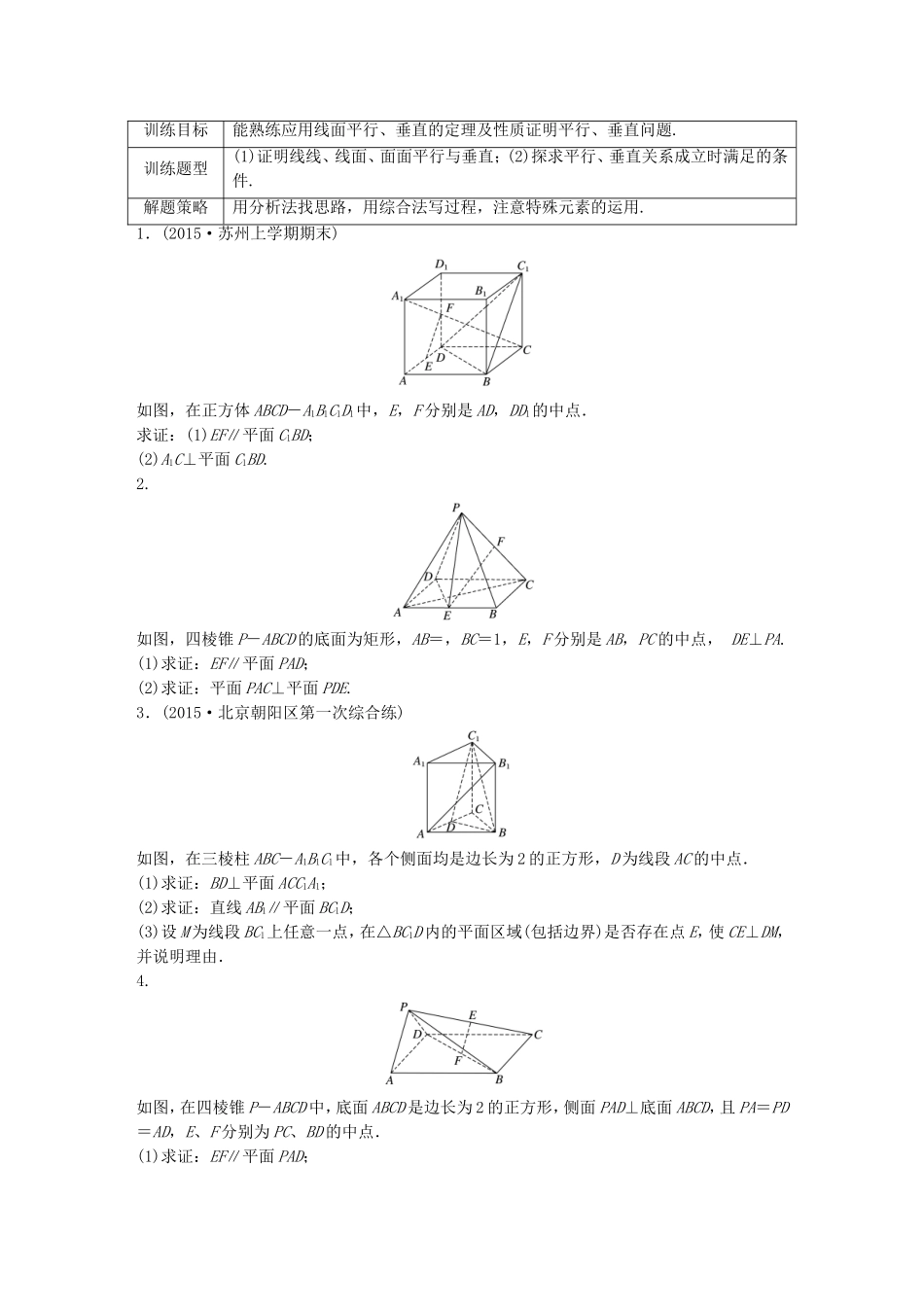
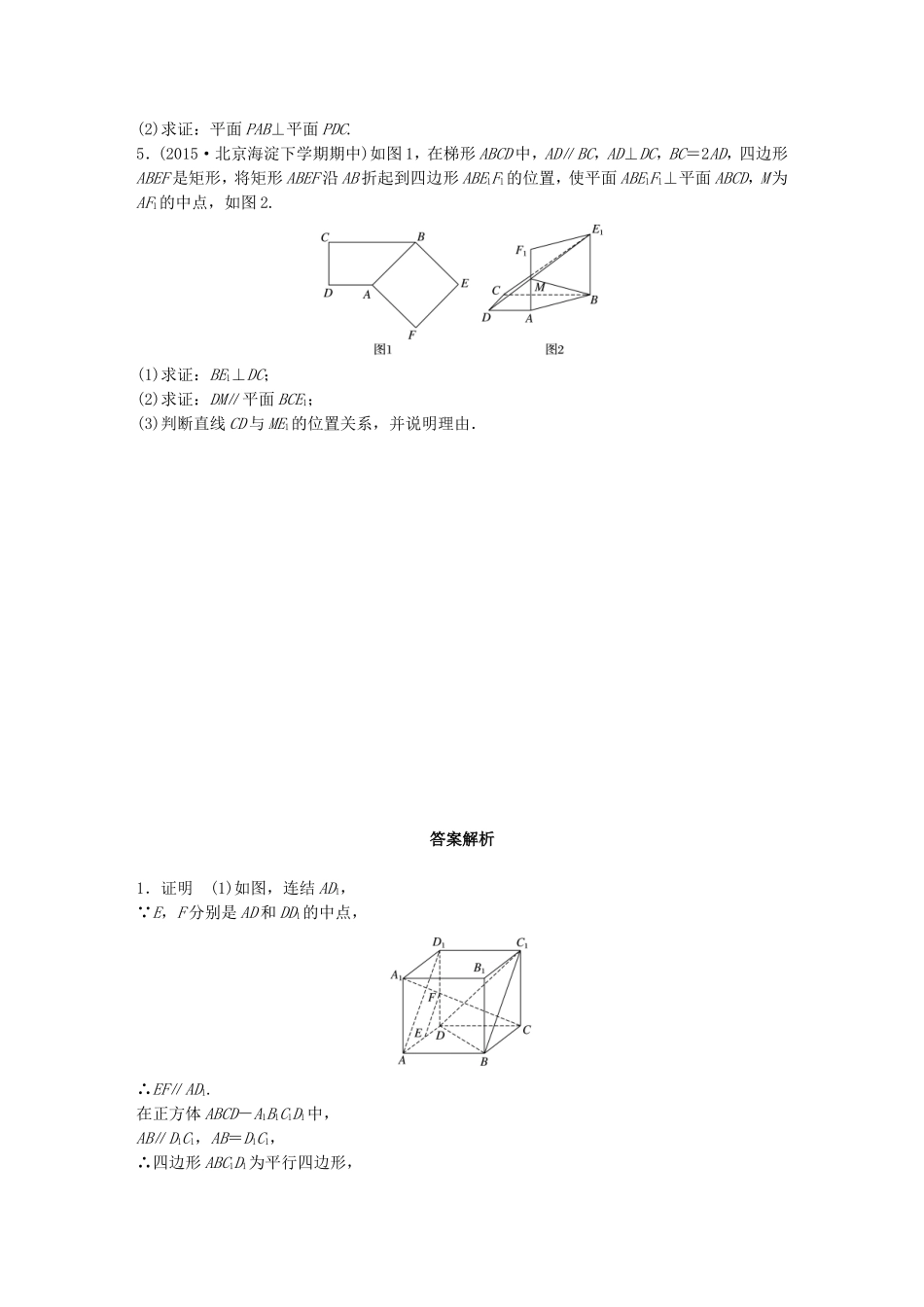
训练目标能熟练应用线面平行、垂直的定理及性质证明平行、垂直问题.训练题型(1)证明线线、线面、面面平行与垂直;(2)探求平行、垂直关系成立时满足的条件.解题策略用分析法找思路,用综合法写过程,注意特殊元素的运用.1.(2015·苏州上学期期末)如图,在正方体ABCD-A1B1C1D1中,E,F分别是AD,DD1的中点.求证:(1)EF∥平面C1BD;(2)A1C⊥平面C1BD.2.如图,四棱锥P-ABCD的底面为矩形,AB=,BC=1,E,F分别是AB,PC的中点,DE⊥PA.(1)求证:EF∥平面PAD;(2)求证:平面PAC⊥平面PDE.3.(2015·北京朝阳区第一次综合练)如图,在三棱柱ABC-A1B1C1中,各个侧面均是边长为2的正方形,D为线段AC的中点.(1)求证:BD⊥平面ACC1A1;(2)求证:直线AB1∥平面BC1D;(3)设M为线段BC1上任意一点,在△BC1D内的平面区域(包括边界)是否存在点E,使CE⊥DM,并说明理由.4.如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=AD,E、F分别为PC、BD的中点.(1)求证:EF∥平面PAD;(2)求证:平面PAB⊥平面PDC.5.(2015·北京海淀下学期期中)如图1,在梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD,四边形ABEF是矩形,将矩形ABEF沿AB折起到四边形ABE1F1的位置,使平面ABE1F1⊥平面ABCD,M为AF1的中点,如图2.(1)求证:BE1⊥DC;(2)求证:DM∥平面BCE1;(3)判断直线CD与ME1的位置关系,并说明理由.答案解析1.证明(1)如图,连结AD1, E,F分别是AD和DD1的中点,∴EF∥AD1.在正方体ABCD-A1B1C1D1中,AB∥D1C1,AB=D1C1,∴四边形ABC1D1为平行四边形,即有AD1∥BC1,∴EF∥BC1.又EF⊄平面C1BD,BC1⊂平面C1BD,∴EF∥平面C1BD.(2)如图,连结AC,则AC⊥BD. 在正方体ABCD-A1B1C1D1中,AA1⊥平面ABCD,BD⊂平面ABCD,∴AA1⊥BD.又AA1∩AC=A,AA1⊂平面AA1C,AC⊂平面AA1C,∴BD⊥平面AA1C,A1C⊂平面AA1C,∴A1C⊥BD.同理可证A1C⊥BC1.又BD∩BC1=B,BD⊂平面C1BD,BC1⊂平面C1BD,∴A1C⊥平面C1BD.2.证明(1)如图,取PD中点G,连结AG,FG,因为F,G分别为PC,PD的中点,所以FG∥CD,且FG=CD.又因为E为AB中点,所以AE∥CD,且AE=CD.所以AE∥FG,AE=FG.所以四边形AEFG为平行四边形.所以EF∥AG,又EF⊄平面PAD,AG⊂平面PAD,所以EF∥平面PAD.(2)设AC∩DE=H,由△AEH∽△CDH及E为AB中点,得==,又因为AB=,BC=1,所以AC=,AH=AC=.所以==,又∠BAC为公共角,所以△HAE∽△BAC.所以∠AHE=∠ABC=90°,即DE⊥AC.又DE⊥PA,PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以DE⊥平面PAC.又DE⊂平面PDE,所以平面PAC⊥平面PDE.3.(1)证明因为三棱柱的侧面是正方形,所以CC1⊥BC,CC1⊥AC,BC∩AC=C,BC⊂底面ABC,AC⊂底面ABC,所以CC1⊥底面ABC.因为BD⊂底面ABC,所以CC1⊥BD.由已知可得,底面三角形ABC为正三角形.因为D是AC中点,所以BD⊥AC.因为AC∩CC1=C,AC⊂平面ACC1A1,CC1⊂平面ACC1A1,所以BD⊥平面ACC1A1.(2)证明如图,连结B1C交BC1于点O,连结OD.显然点O为B1C的中点.因为D是AC中点,所以AB1∥OD.因为OD⊂平面BC1D,AB1⊄平面BC1D,所以直线AB1∥平面BC1D.(3)解在△BC1D内的平面区域(包括边界)存在一点E,使CE⊥DM,此时点E在线段C1D上.证明如下:如图,过C作CE⊥C1D,交线段C1D于E,由(1)可知BD⊥平面ACC1A1,而CE⊂平面ACC1A1,所以BD⊥CE.又CE⊥C1D,C1D∩BD=D,C1D⊂平面BC1D,BD⊂平面BC1D,所以CE⊥平面BC1D.又DM⊂平面BC1D,所以CE⊥DM.4.证明(1)如图,连结AC,则AC∩BD=F,因为四边形ABCD为正方形,所以F为AC的中点,又E为PC的中点,所以在△CPA中,EF∥PA.又PA⊂侧面PAD,EF⊄侧面PAD,所以EF∥侧面PAD.(2)因为四边形ABCD为正方形,所以CD⊥AD,因为侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,CD⊂底面ABCD,所以CD⊥侧面PAD.又PA⊂侧面PAD,所以CD⊥PA.又PA=PD=AD,所以△PAD是等腰直角三角形,且∠APD=,即PA⊥PD.因为CD∩PD=D,且CD⊂侧面PDC,PD⊂侧面PDC,所以PA⊥侧面PDC.又PA⊂侧面PAB,所以侧面PAB⊥侧面PDC.即平面PAB⊥平面PDC.5.(1)证明因为四边形ABE1F1为矩形,所以BE1⊥AB.因为平面ABCD⊥平面ABE1F1,且平面ABCD∩平...