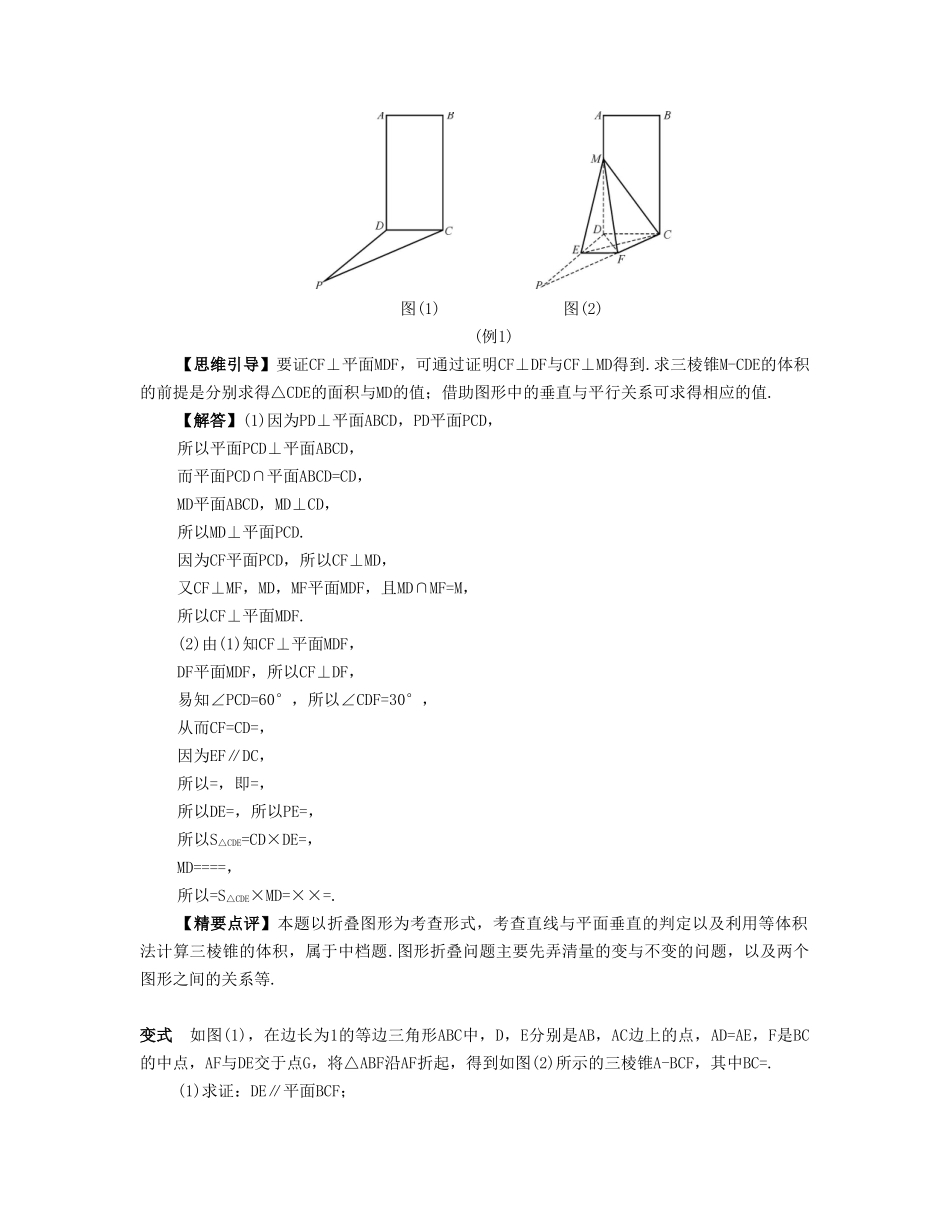
第53课立体几何综合(本课时对应学生用书第页)自主学习回归教材1.(必修2P38练习5改编)如图,在△ABC中,M为边BC的中点,沿AM将△ABC折起,使点B在平面ACM外.则当时,直线AM⊥平面BCM.(第1题)【答案】AB=AC【解析】当AB=AC时,有AM⊥MB,AM⊥MC.2.(必修2P50练习5改编)若在三棱锥S-ABC中,M,N,P分别是棱SA,SB,SC的中点,则平面MNP与平面ABC的位置关系为.【答案】平行3.(必修2P70练习13改编)若三个球的半径之比为1∶2∶3,则最大的球的体积是另外两个球的体积之和的倍.【答案】3【解析】根据球的体积公式V=πr3进行求解.4.如图(1),已知正三棱柱ABC-A1B1C1的底面边长为2cm,高为5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为cm.(第4题(1))【答案】13【解析】如图(2),将三棱柱沿侧棱AA1展开(两周),AA1=5cm,AA″=12cm,易知所求最短路线长为A1A″=13cm.(第4题(2))1.高考中关于立体几何的常考考点有:性质的运用,证明位置关系(平行或垂直),求量(体积、面积、长度).2.解决翻折问题时要注意量和关系的变与不变.3.立体几何会与函数等知识综合考查求最值,得出关系式是解决问题的前提.【要点导学】要点导学各个击破简单几何体的折叠问题例1(2014·广东卷)如图(1),四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2,如图(2)所示折叠,折痕EF∥DC.其中点E,F分别在线段PD,PC上,沿EF折叠后点P在线段AD上的点记为M,并且MF⊥CF.(1)求证:CF⊥平面MDF;(2)求三棱锥M-CDE的体积.图(1)图(2)(例1)【思维引导】要证CF⊥平面MDF,可通过证明CF⊥DF与CF⊥MD得到.求三棱锥M-CDE的体积的前提是分别求得△CDE的面积与MD的值;借助图形中的垂直与平行关系可求得相应的值.【解答】(1)因为PD⊥平面ABCD,PD平面PCD,所以平面PCD⊥平面ABCD,而平面PCD∩平面ABCD=CD,MD平面ABCD,MD⊥CD,所以MD⊥平面PCD.因为CF平面PCD,所以CF⊥MD,又CF⊥MF,MD,MF平面MDF,且MD∩MF=M,所以CF⊥平面MDF.(2)由(1)知CF⊥平面MDF,DF平面MDF,所以CF⊥DF,易知∠PCD=60°,所以∠CDF=30°,从而CF=CD=,因为EF∥DC,所以=,即=,所以DE=,所以PE=,所以S△CDE=CD×DE=,MD====,所以=S△CDE×MD=××=.【精要点评】本题以折叠图形为考查形式,考查直线与平面垂直的判定以及利用等体积法计算三棱锥的体积,属于中档题.图形折叠问题主要先弄清量的变与不变的问题,以及两个图形之间的关系等.变式如图(1),在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图(2)所示的三棱锥A-BCF,其中BC=.(1)求证:DE∥平面BCF;(2)求证:CF⊥平面ABF;(3)当AD=时,求三棱锥F-DEG的体积.图(1)图(2)(变式)【思维引导】要证DE∥平面BCF,即可证DE∥BC;要证CF⊥平面ABF,即可证AF⊥CF与BF⊥CF;求体积前先确定GE是高,△DFG是底.【解答】(1)在等边三角形ABC中,AD=AE,所以=,在折叠后的三棱锥A-BCF中也成立,所以DE∥BC.因为DE平面BCF,BC平面BCF,所以DE∥平面BCF.(2)在等边三角形ABC中,F是BC的中点,所以AF⊥CF①,且BF=CF=.因为在三棱锥A-BCF中,BC=,所以BC2=BF2+CF2,所以CF⊥BF②.因为BF∩AF=F,BF,AF平面ABF,所以CF⊥平面ABF.(3)由(1)可知GE∥CF,结合(2)可得GE⊥平面DFG,所以==××DG×FG×GE=×××××=.立体几何模型实际应用问题例2请你设计一个包装盒,ABCD是边长为60cm的正方形硬纸片,切去如图(1)所示的阴影部分的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个如图(2)所示的正四棱柱形状的包装盒,E,F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.(1)若广告商要求包装盒侧面积S(单位:cm2)最大,试问:x应取何值?(2)若广告商要求包装盒容积V(单位:cm3)最大,试问:x应取何值?并求出此时包装盒的高与底面边长的比值.图(1)图(2)(例2)【思维引导】本题求解的前提是找到盒子的底面边长与高,继而求得底面面积,再求其体积.而解题的关键是正确地求得“盒子”体积的函数式.因为题中涉及了三次函数的最值,所以要考虑结合导数求最值.【解答】(1)根据题意...