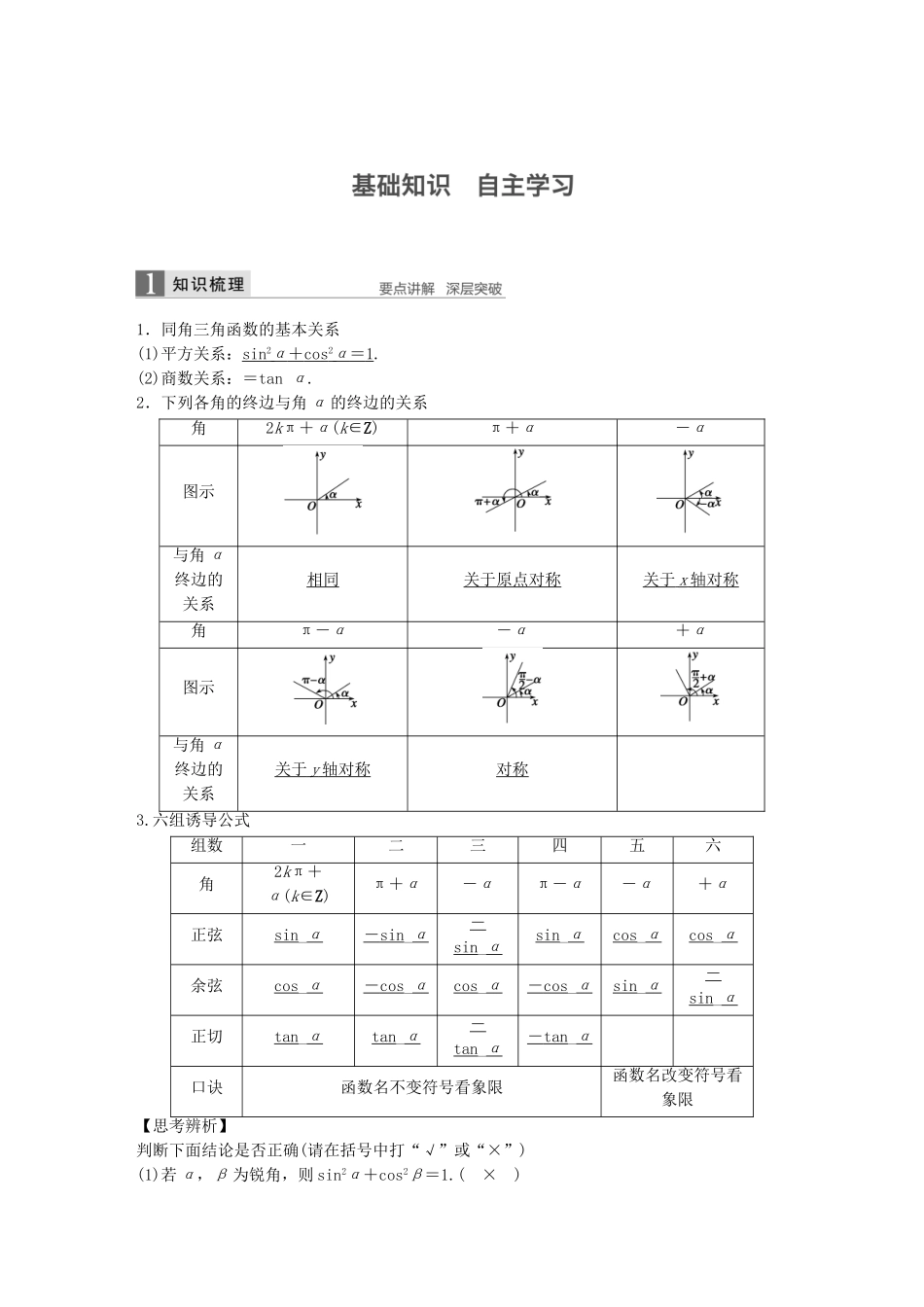
1.同角三角函数的基本关系(1)平方关系:sin2α+cos2α=1.(2)商数关系:=tanα.2.下列各角的终边与角α的终边的关系角2kπ+α(k∈Z)π+α-α图示与角α终边的关系相同关于原点对称关于x轴对称角π-α-α+α图示与角α终边的关系关于y轴对称对称3.六组诱导公式组数一二三四五六角2kπ+α(k∈Z)π+α-απ-α-α+α正弦sin_α-sin_α-sin_αsin_αcos_αcos_α余弦cos_α-cos_αcos_α-cos_αsin_α-sin_α正切tan_αtan_α-tan_α-tan_α口诀函数名不变符号看象限函数名改变符号看象限【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)若α,β为锐角,则sin2α+cos2β=1.(×)(2)若α∈R,则tanα=恒成立.(×)(3)sin(π+α)=-sinα成立的条件是α为锐角.(×)(4)六组诱导公式中的角α可以是定义域内的任意角.(√)(5)诱导公式的记忆口诀中“奇变偶不变,符号看象限”,其中的奇、偶是指的奇数倍和偶数倍,变与不变指函数名称的变化.(√)1.(教材改编)已知α是第二象限角,sinα=,则cosα=________.答案-解析 sinα=,α是第二象限角,∴cosα=-=-.2.已知=-,那么的值是________.答案解析由于·==-1,故=.3.已知sin(π-α)=log8,且α∈(-,0),则tan(2π-α)的值为________.答案解析sin(π-α)=sinα=log8=-,又α∈(-,0),得cosα==,tan(2π-α)=tan(-α)=-tanα=-=.4.已知cos=,则sin=________.答案-解析 +=-,∴α-=--,∴sin=sin=-sin=-cos=-.5.已知函数f(x)=则f(f(2016))=________.答案-1解析 f(f(2016))=f(2016-16)=f(2000),∴f(2000)=2cos=2cosπ=-1.题型一同角三角函数关系式的应用例1(1)已知tanθ=2,则sin2θ+sinθcosθ-2cos2θ=________.(2)已知sinαcosα=,且<α<,则cosα-sinα的值为________.答案(1)(2)解析(1)由于tanθ=2,则sin2θ+sinθcosθ-2cos2θ=====.(2) <α<,∴cosα<0,sinα<0且cosα>sinα,∴cosα-sinα>0.又(cosα-sinα)2=1-2sinαcosα=1-2×=,∴cosα-sinα=.思维升华(1)利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用=tanα可以实现角α的弦切互化.(2)应用公式时注意方程思想的应用:对于sinα+cosα,sinαcosα,sinα-cosα这三个式子,利用(sinα±cosα)2=1±2sinαcosα,可以知一求二.(3)注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.已知sinα-cosα=,α∈(0,π),则tanα=________.答案-1解析由消去sinα得:2cos2α+2cosα+1=0,即(cosα+1)2=0,∴cosα=-.又α∈(0,π),∴α=,∴tanα=tan=-1.题型二诱导公式的应用例2(1)已知sin=,则cos的值为________.(2)已知A=+(k∈Z),则A的值构成的集合是__________.答案(1)-(2){2,-2}解析(1)cos=cos=-sin=-.(2) 当k为偶数时,A=+=2;当k为奇数时,A=-=-2.∴A的值构成的集合是{2,-2}.思维升华(1)诱导公式用法的一般思路①化大角为小角.②角中含有加减的整数倍时,用公式去掉的整数倍.(2)常见的互余和互补的角①常见的互余的角:-α与+α;+α与-α;+α与-α等.②常见的互补的角:+θ与-θ;+θ与-θ等.(1)已知sin=,则cos=________.(2)sin(-1200°)cos1290°+cos(-1020°)sin(-1050°)=________.答案(1)(2)1解析(1) +=,∴cos=cos=sin=.(2)原式=-sin1200°cos1290°-cos1020°sin1050°=-sin(3×360°+120°)cos(3×360°+210°)-cos(2×360°+300°)sin(2×360°+330°)=-sin120°cos210°-cos300°sin330°=-sin(180°-60°)cos(180°+30°)-cos(360°-60°)×sin(360°-30°)=sin60°cos30°+cos60°sin30°=×+×=1.题型三同角三角函数关系式、诱导公式的综合应用例3(1)已知α为锐角,且有2tan(π-α)-3cos(+β)+5=0,tan(π+α)+6sin(π+β)-1=0,则sinα=________.(2)已知sinα是方程5x2-7x-6=0的根,α是第三象限角,则·tan2(π-α)=___...