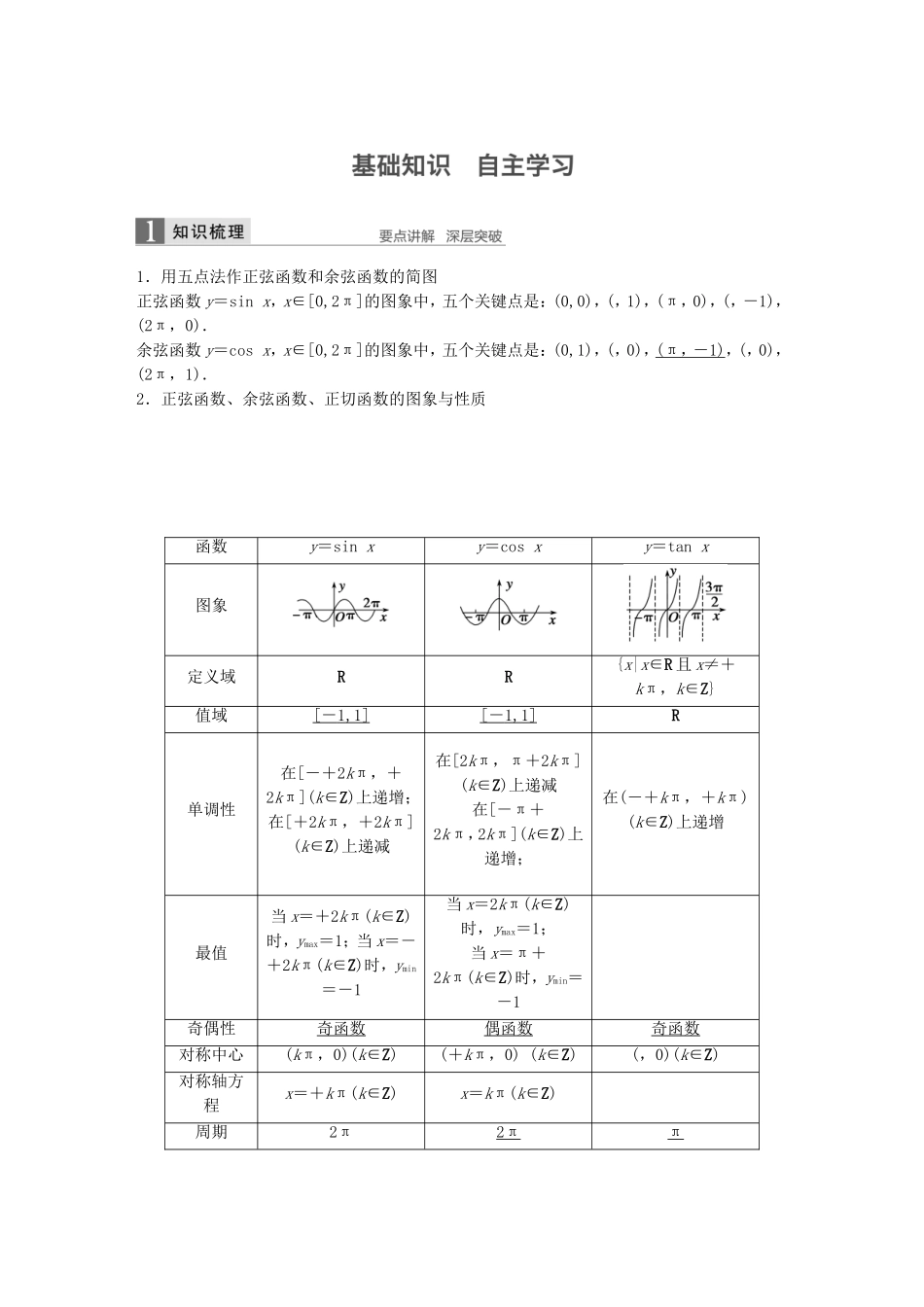
1.用五点法作正弦函数和余弦函数的简图正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:(0,0),(,1),(π,0),(,-1),(2π,0).余弦函数y=cosx,x∈[0,2π]的图象中,五个关键点是:(0,1),(,0),(π,-1),(,0),(2π,1).2.正弦函数、余弦函数、正切函数的图象与性质函数y=sinxy=cosxy=tanx图象定义域RR{x|x∈R且x≠+kπ,k∈Z}值域[-1,1][-1,1]R单调性在[-+2kπ,+2kπ](k∈Z)上递增;在[+2kπ,+2kπ](k∈Z)上递减在[2kπ,π+2kπ](k∈Z)上递减在[-π+2kπ,2kπ](k∈Z)上递增;在(-+kπ,+kπ)(k∈Z)上递增最值当x=+2kπ(k∈Z)时,ymax=1;当x=-+2kπ(k∈Z)时,ymin=-1当x=2kπ(k∈Z)时,ymax=1;当x=π+2kπ(k∈Z)时,ymin=-1奇偶性奇函数偶函数奇函数对称中心(kπ,0)(k∈Z)(+kπ,0)(k∈Z)(,0)(k∈Z)对称轴方程x=+kπ(k∈Z)x=kπ(k∈Z)周期2π2ππ【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)y=sinx在第一、第四象限是增函数.(×)(2)常数函数f(x)=a是周期函数,它没有最小正周期.(√)(3)正切函数y=tanx在定义域内是增函数.(×)(4)已知y=ksinx+1,x∈R,则y的最大值为k+1.(×)(5)y=sin|x|是偶函数.(√)(6)若sinx>,则x>.(×)1.(教材改编)函数f(x)=4-2cosx的最小值是,取得最小值时,x的取值集合为.答案2{x|x=6kπ,k∈Z}解析 -1≤cosx≤1,∴f(x)min=4-2×1=2,此时的cosx=1,x=2kπ,∴x=6kπ,k∈Z.2.(2015·扬州模拟)函数y=lg(sinx-cosx)的定义域为.答案解析sinx-cosx>0,即sinx>cosx.画出y=sinx及y=cosx在[0,2π]上的图象如图.由图象知原函数的定义域为.3.若函数f(x)=sinωx(ω>0)在区间[0,]上单调递增,在区间[,]上单调递减,则ω=.答案解析 f(x)=sinωx(ω>0)过原点,∴当0≤ωx≤,即0≤x≤时,y=sinωx是增函数;当≤ωx≤,即≤x≤时,y=sinωx是减函数.由f(x)=sinωx(ω>0)在上单调递增,在上单调递减知,=,∴ω=.4.函数y=2sin(x∈[-π,0])的单调递减区间是.答案解析 由题意知2kπ+≤2x+≤2kπ+(k∈Z),∴kπ+≤x≤kπ+(k∈Z).又x∈[-π,0],∴-≤x≤-.5.函数f(x)=2sin-m在x∈内有两个不同的零点,则m的取值范围是.答案[1,2)解析令f(x)=0,则m=2sin.因为x∈,故-≤2x-≤,设2x-=t,则m=2sint,t∈,根据题意并结合函数图象(图略)可知m的取值范围是[1,2).题型一三角函数的定义域和值域例1(1)函数y=的定义域为.(2)函数f(x)=3sin在区间[0,]上的值域为.(3)函数y=cos2x+sinx(|x|≤)的最小值为.答案(1)(k∈Z)(2)(3)解析(1)由2sinx-1≥0,得sinx≥,所以2kπ+≤x≤2kπ+(k∈Z).(2)当x∈时,2x-∈,sin∈,故3sin∈,即此时函数f(x)的值域是.(3)令t=sinx, |x|≤,∴t∈.∴y=-t2+t+1=-2+,∴t=-时,ymin=.思维升华(1)三角函数定义域的求法求三角函数定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图象来求解.(2)三角函数值域的不同求法①利用sinx和cosx的值域直接求;②把所给的三角函数式变换成y=Asin(ωx+φ)的形式求值域;③通过换元,转换成二次函数求值域.(1)函数y=lg(sinx)+的定义域为.(2)函数y=sinx-cosx+sinxcosx的值域为.答案(1)(2)解析(1)要使函数有意义必须有即解得∴2kπ<x≤+2kπ(k∈Z),∴函数的定义域为.(2)设t=sinx-cosx,则t2=sin2x+cos2x-2sinxcosx,sinxcosx=,且-≤t≤.∴y=-+t+=-(t-1)2+1.当t=1时,ymax=1;当t=-时,ymin=--.∴函数的值域为.题型二三角函数的单调性例2(1)函数f(x)=tan的单调递增区间是.(2)已知ω>0,函数f(x)=sin在上单调递减,则ω的取值范围是.答案(1)(k∈Z)(2)解析(1)由kπ-<2x-<kπ+(k∈Z)得,-<x<+(k∈Z),所以函数f(x)=tan的单调递增区间为(k∈Z).(2)由<x<π,ω>0得,+<ωx+<ωπ+,又y=sinx在上递减,所以解得≤ω≤.思维升华(1)已知三角函数解析式求单调区间:①求函数的单调区间应遵循简单化原则,将解析式先化简,并注意复合函数单调性规律“...