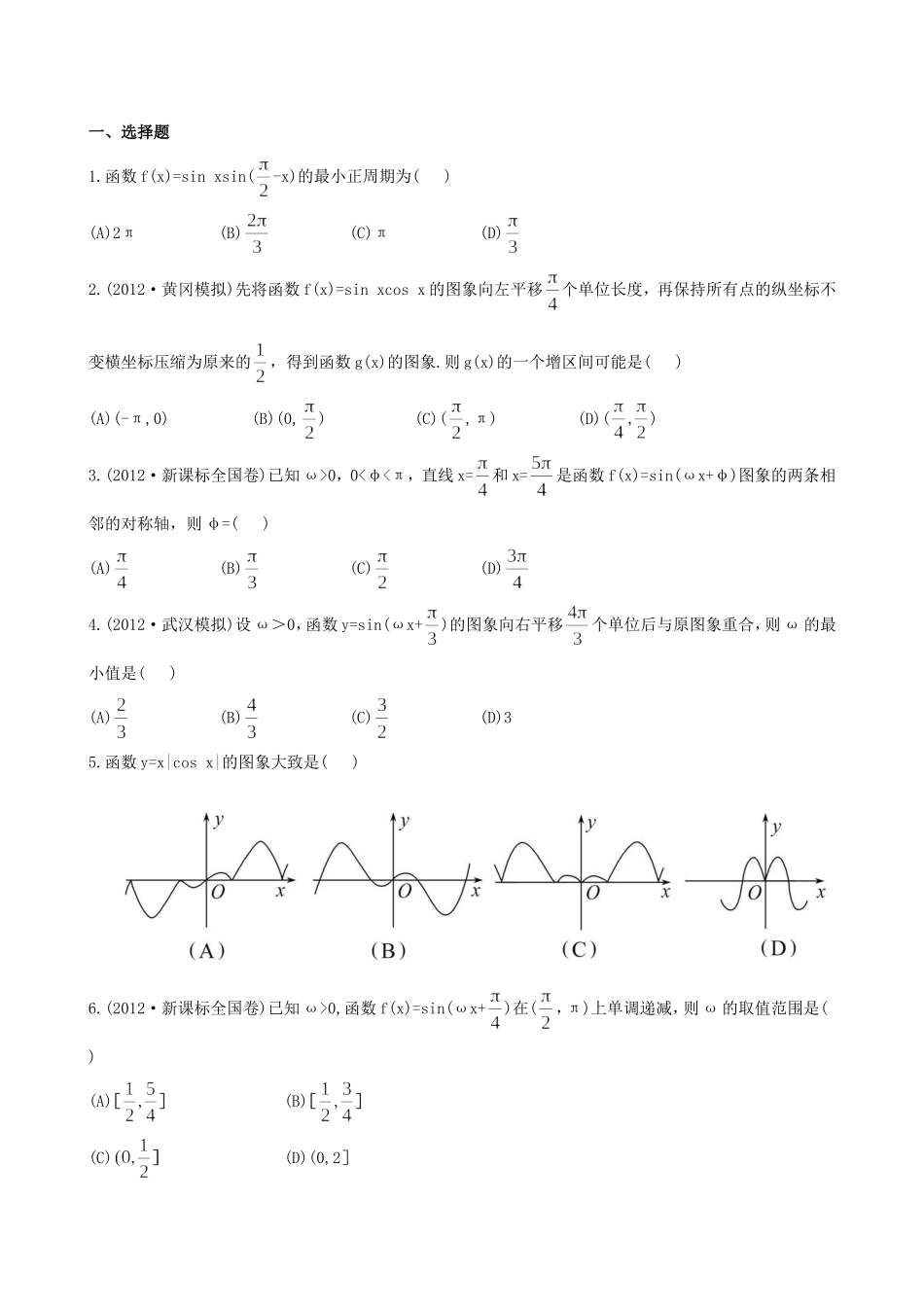
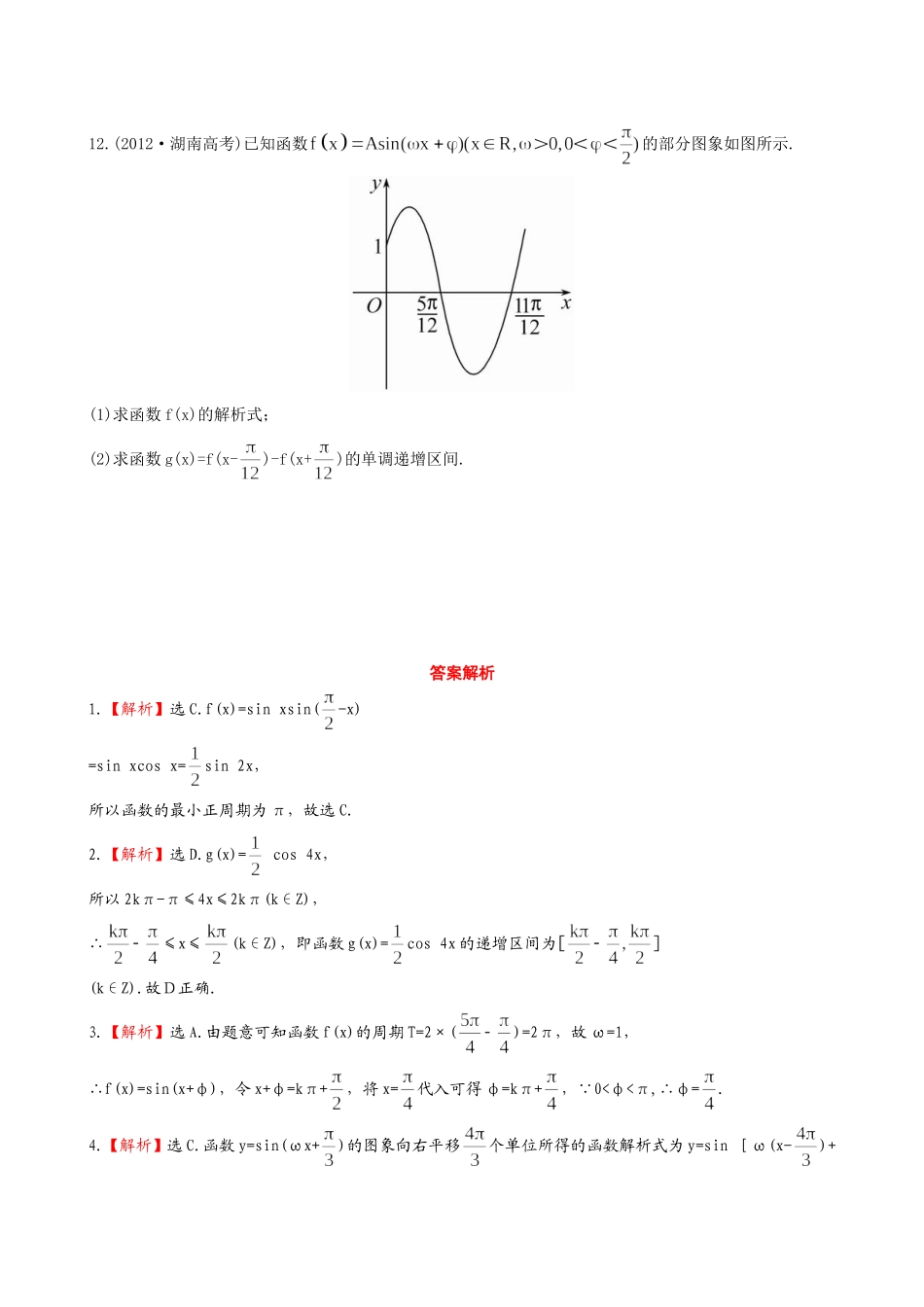
一、选择题1.函数f(x)=sinxsin(-x)的最小正周期为()(A)2π(B)(C)π(D)2.(2012·黄冈模拟)先将函数f(x)=sinxcosx的图象向左平移个单位长度,再保持所有点的纵坐标不变横坐标压缩为原来的,得到函数g(x)的图象.则g(x)的一个增区间可能是()(A)(-π,0)(B)(0,)(C)(,π)(D)()3.(2012·新课标全国卷)已知ω>0,0<φ<π,直线x=和x=是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,则φ=()(A)(B)(C)(D)4.(2012·武汉模拟)设ω>0,函数y=sin(ωx+)的图象向右平移个单位后与原图象重合,则ω的最小值是()(A)(B)(C)(D)35.函数y=x|cosx|的图象大致是()6.(2012·新课标全国卷)已知ω>0,函数f(x)=sin(ωx+)在(,π)上单调递减,则ω的取值范围是()(A)(B)(C)(D)(0,2]二、填空题7.函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则f()的值是.8.已知函数f(x)=sin(ωx+)(ω>0),若函数f(x)图象上的一个对称中心到对称轴的距离的最小值为,则ω的值为.9.关于f(x)=3sin(2x+),有以下命题:①若,则=kπ(k∈Z);②f(x)图象与g(x)=3cos(2x-)图象相同;③f(x)在区间上是减函数;④f(x)图象关于点(-,0)对称.其中正确的命题是.三、解答题10.(2012·湖北高考)设函数f(x)=+ωx·cosωx-+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(,1).(1)求函数f(x)的最小正周期;(2)若y=f(x)的图象经过点(,0),求函数f(x)的值域.11.(2012·咸宁模拟)设函数的最小正周期为.(1)求ω的值;(2)若函数y=g(x)的图象是由y=f(x)的图象向右平移个单位长度得到的,求y=g(x)的单调增区间.12.(2012·湖南高考)已知函数的部分图象如图所示.(1)求函数f(x)的解析式;(2)求函数g(x)=f(x-)-f(x+)的单调递增区间.答案解析1.【解析】选C.f(x)=sinxsin(-x)=sinxcosx=sin2x,所以函数的最小正周期为π,故选C.2.【解析】选D.g(x)=cos4x,所以2kπ-π≤4x≤2kπ(k∈Z),∴≤x≤(k∈Z),即函数g(x)=cos4x的递增区间为(k∈Z).故D正确.3.【解析】选A.由题意可知函数f(x)的周期T=2×()=2π,故ω=1,∴f(x)=sin(x+φ),令x+φ=kπ+,将x=代入可得φ=kπ+,∵0<φ<π,∴φ=.4.【解析】选C.函数y=sin(ωx+)的图象向右平移个单位所得的函数解析式为y=sin[ω(x-)+]=sin[(ωx+)-ω],又函数y=sin(ωx+)的图象向右平移个单位后与原图象重合,∴ω=2kπ(k∈Z)⇒ω=k(k∈Z),∵ω>0,∴ω的最小值为,故选C.5.【解析】选A.∵函数y=x|cosx|是奇函数,故图象关于原点对称.从而排除C,D两个选项;又当x>0时,y=x|cosx|≥0.从而排除B选项,故选A.6.【解析】选A.结合y=sinωx的图象可知y=sinωx在上单调递减,而可知y=sinωx图象向左平移个单位之后可得y=sin(ωx+)的图象,故y=sin(ωx+)在上递减,故应有解得≤ω≤.7.【解析】由图象可知A=所以T=π=,ω=2,所以f(x)=(2x+φ),所以所以φ=,所以答案:8.【解析】函数f(x)图象上的一个对称中心到对称轴的距离的最小值为由题意可知答案:9.【解析】①不正确,可关于对称轴对称;=3sin(2x+),故②正确;当x∈时,2x+∴f(x)在区间上是减函数,故③正确;当x=-时,2x+=0,∴④正确.答案:②③④10.【解析】(1)因为=2sin(2ωx-)+λ,由直线x=π是y=f(x)图象的一条对称轴,可得sin(2ωπ-)=±1.所以即又ω∈(,1),所以ω=.所以f(x)的最小正周期是.(2)由y=f(x)的图象过点(,0),得f()=0,即λ=-2sin()=-2sin=-,即λ=-.故f(x)=2sin函数f(x)的值域为11.【解析】(1)==依题意得=,故ω的值为.(2)依题意得:g(x)==由2kπ-≤3x-≤2kπ+(k∈Z),解得kπ+≤x≤kπ+(k∈Z).故y=g(x)的单调增区间为(k∈Z).12.【解析】(1)由图象知,周期T=2=π,所以ω==2,因为点(,0)在函数图象上,所以即又因为0<φ<,所以从而+φ=π,即φ=.又点(0,1)在函数图象上,所以Asin=1,得A=2,故函数f(x)的解析式为f(x)=2sin(2x+).(2)=2sin2x-2sin(2x+)=2sin2x-2=sin2x-2x=2sin(2x-).由2kπ-≤2x-≤2kπ+,k∈Z,得kπ-≤x≤kπ+(k∈Z).所以函数g(x)的单调递增区间是(k∈Z).