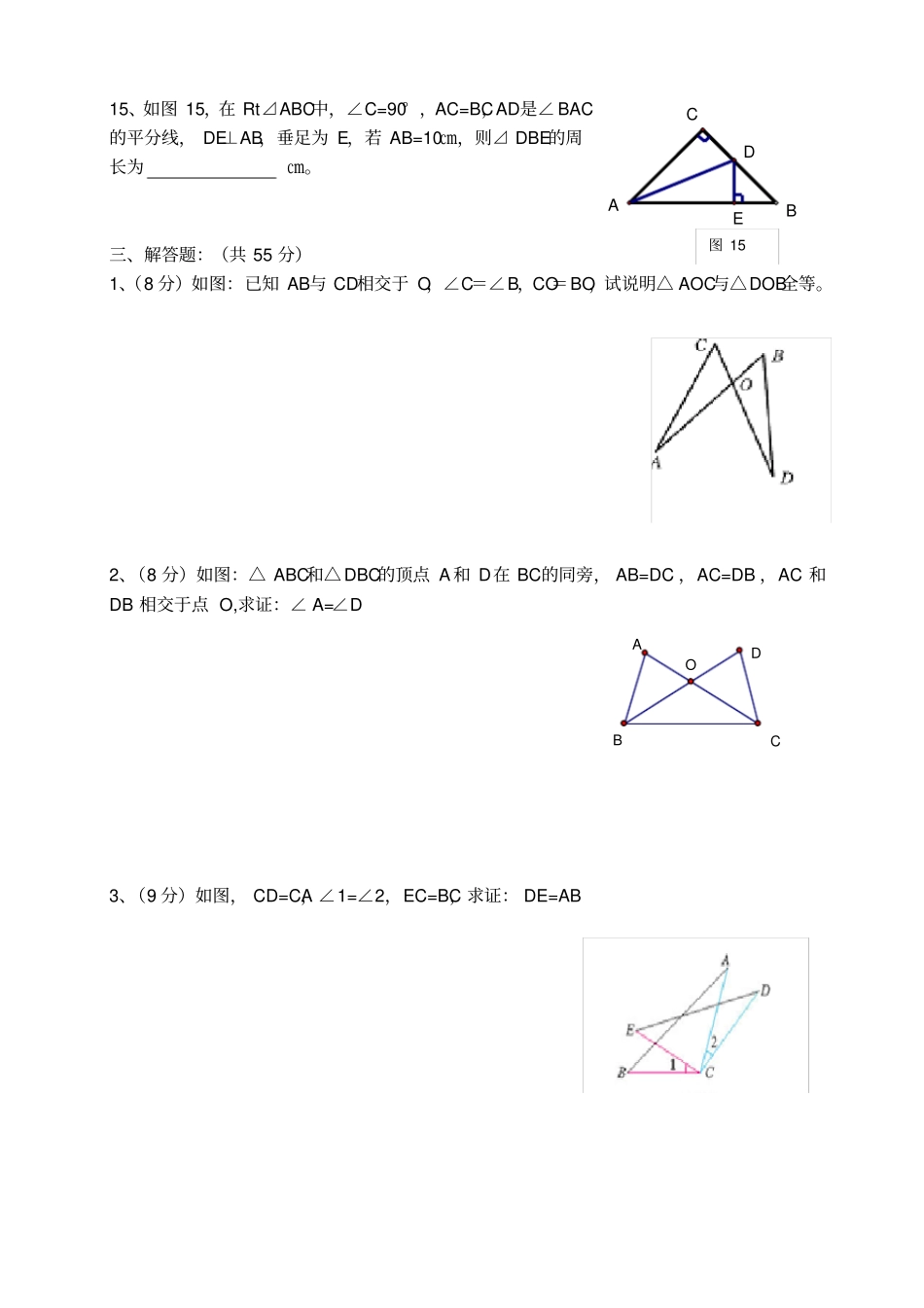
2009学年第一学期八年级数学第十一章《全等三角形》单元练习班级:学号:姓名:一、选择题:(每题3分,共30分)1、如图1,若ABC≌DEF,则)(EA、30B、62C、92D、882、如图2,△ABC≌△DCB,A、B的对应顶点分别为点D、C,如果AB=7cm,BC=12cm,AC=9cm,那么BD的长是()。A、7cmB、9cmC、12cmD、无法确定3、如图3,线段AC与BD交于点O,且OA=OC,请添加一个条件,使OAB≌OCD,这个条件不可以是()A、CDABB、ODOBC、CAD、DB4、如图4,点P是BAC内一点,PFPEACPFABPE,,,则PEA≌PFA的理由是()A、HLB、ASAC、AASD、SAS5、如图5,∠1=∠2,PD⊥OA于D,PE⊥OB于E,垂足分别为D、E,下列结论错误的是()A、PD=PEB、OD=OEC、∠DPO=∠EPOD、PD=OD6、图6中全等的三角形是()A、Ⅰ和ⅡB、Ⅱ和ⅣC、Ⅱ和ⅢD、Ⅰ和Ⅲ图5FEDCBA30°62°图1CABOD图3PBCFEA图45cm5cm9cm9cm8cm8cm8cm8cmⅣⅢⅡⅠ303030图6图27、如图7,∠B=∠D,∠1=∠2,则ABC≌ADC的理由是()A、AASB、HLC、ASAD、SAS8、如图8,AC与BD相交于点E,ECAEEDBE,,则ABE≌CDE的理由是()A、ASAB、SASC、AASD、SSS9、如图9,如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是()A、带①去B、带②去C、带③去D、带①和②去10、如图10,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,∠1=∠2,图中全等三角形共有()A、1对B、2对C、3对D、4对二、填空题:(每题3分,共15分)11、如图11,AB=AC,要证△ABD≌△ACD还需添加的一个条件可以是:(填出一种即可)。12、如图12,在△ABC和△DEF中,如果AB=DE,AC=DF,只要再具备条件,就可以证明△ABC≌△DEF。13、如图13,AB=AC,BD=DC,若28B,则C.14、如图14,长方形ABCD沿AE折叠,使点D落在BC.边上的F点处,如果∠BAF=60°,则∠DAE=。ABCD图13ADCB图11ABCDFE图14BFADCE图12图912OABCDE图10图8DCBA12图715、如图15,在Rt⊿ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=10㎝,则⊿DBE的周长为㎝。三、解答题:(共55分)1、(8分)如图:已知AB与CD相交于O,∠C=∠B,CO=BO,试说明△AOC与△DOB全等。2、(8分)如图:△ABC和△DBC的顶点A和D在BC的同旁,AB=DC,AC=DB,AC和DB相交于点O,求证:∠A=∠D3、(9分)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=ABOBCADBCADE图15FEDCBA4、(10分)如图,已知△ABC中,∠ACB=90°,BD平分∠ABC,DE⊥AB,ED的延长线交BC的延长线于F,求证:AE=CF5、(10分)如图、在B、C、E、F在同一直线上,DEAB//,DFAC//,CEBF求证:DEAB6、(10分)如图,∠BAC=90°,AB=AC,D在AC上,E在BA的延长线上,BD=CE,BD延长线交CE于F,求证:BF⊥CE。[注明:图中标注的∠1、∠2能不能给你启发呢?]广州市天河区教育局教研室编印翻印必究DBFACE12DBCEAF答案:一、选择题:题号12345678910答案DBAADDABCD二、填空:题号1112131415答案CD=DB或∠CAD=∠BADBC=EF或BE=CF或∠A=∠D28°15°10㎝三、1、证明:在△AOC与△DOB中:AOBDOCCOBOCB∴△AOC≌△DOB(ASA)2、证明:在△ABC和△DBC中:ABDCACDBBCCB∴△ABC≌△DCB(SSS)3、证明:∵∠1=∠2∴∠1+∠ACE=∠2+∠ACE∴∠ACB=∠DCE在△ABC和△DBC中:ACB=DCEACDCECBC∴△ABC≌△DCB(SAS)4、证明:∵BD平分∠ABC,DE⊥AB,∠ACB=90°∴DE=DC,∠AED=∠FCD=90°在Rt△AED和Rt△FCD中,AED=FCDDE=DCAED=FCD∴△AED≌△FCD(ASA)5、证明:∵DEAB//∴∠B=∠E∵//ACDF∴∠1=∠2∴∠3=∠4∵BFCE∴BF-CF=CE-CF∴BC=EF在△ABC和△DBC中:B=EBC=F1=2∴△ABC≌△DCB(SAS)∴DEAB6、证明:∵∠BAC=90°∴∠EAC=∠BAD=90°在Rt△AED和Rt△FCD中,BD=CEAB=AC∴Rt△AED≌Rt△FCD(HL)∴∠1=∠2∵∠1+∠ADB=90°∠FDC=∠ADB∴∠2+∠FDC=90°∴∠DFC=90°∴BF⊥CE12DBCEAF