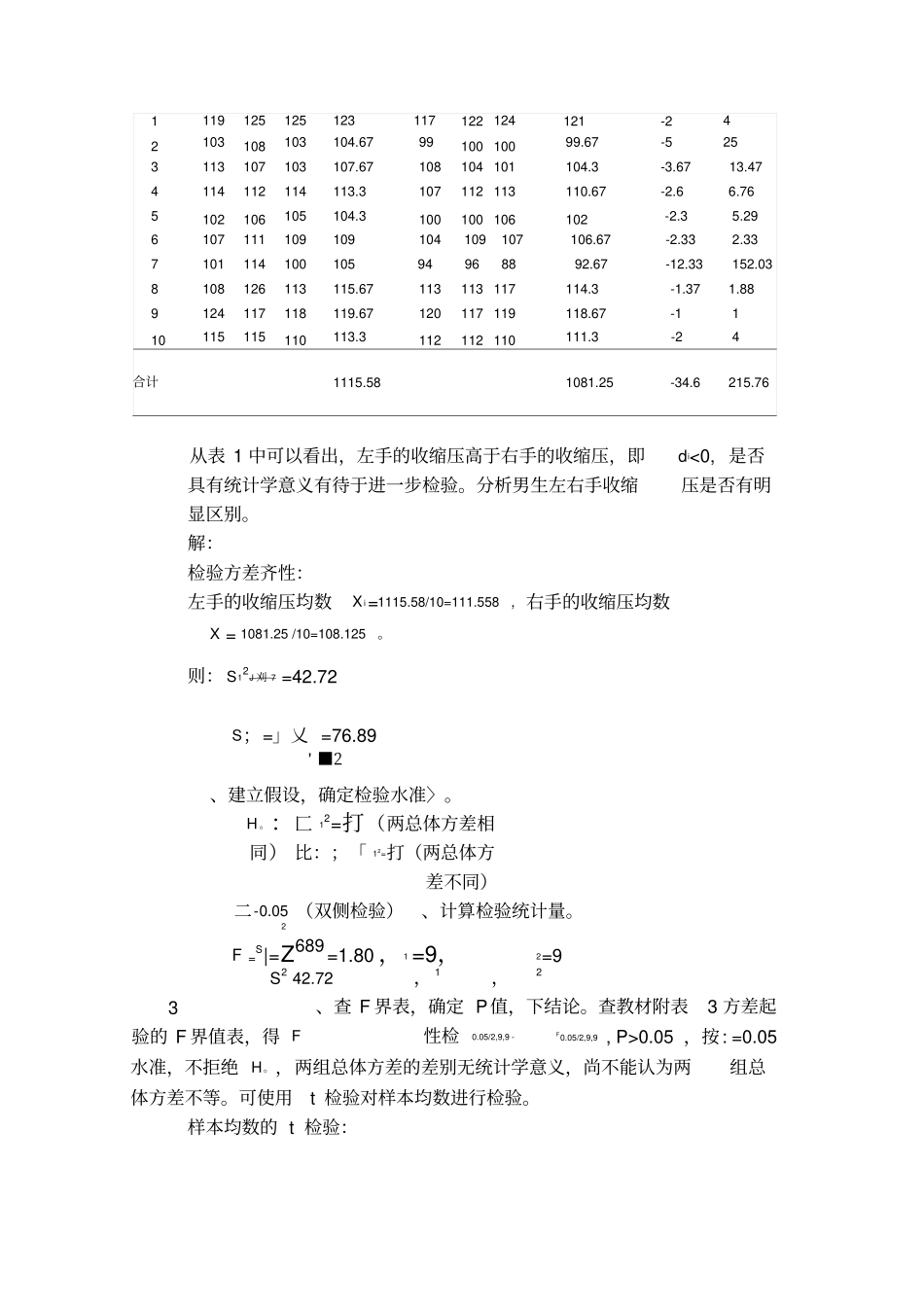
编号左手收缩压平均(X1i)右手收缩压平均(X2i)差(胡=X2i-X1i)营研究题目:心脏在人体解剖方位上的不对称性与左右手血压的测量值之间的关系研究方法和研究条件:通过对10名男生在相同条件下左右手血压值的统计测量以及数据分析来研究此课题。1.测试对象必须惯用右手,既不能是俗称的“左撇子”。2.统一在中午饭过后的静息条件下采集数据。3.考虑到腕式血压计误差较大,对偏大或偏小的血压测量值应该舍去重测。4.由于设备以及研究人员的条件限制,无法采集到大样本的数据,结合数据自身特点,将使用t检验和f检验对数据进行分析。测量数据及分析:表110位男生(惯用右手)在相同条件下左右手收缩压测量的结果1119125125123117122124121-242103108103104.679910010099.67-5253113107103107.67108104101104.3-3.6713.474114112114113.3107112113110.67-2.66.765102106105104.3100100106102-2.35.296107111109109104109107106.67-2.332.33710111410010594968892.67-12.33152.038108126113115.67113113117114.3-1.371.889124117118119.67120117119118.67-1110115115110113.3112112110111.3-24合计1115.581081.25-34.6215.76从表1中可以看出,左手的收缩压高于右手的收缩压,即di<0,是否具有统计学意义有待于进一步检验。分析男生左右手收缩压是否有明显区别。解:检验方差齐性:左手的收缩压均数Xi=1115.58/10=111.558,右手的收缩压均数X=1081.25/10=108.125。则:S12J刈7=42.72S;=」乂=76.89'■2、建立假设,确定检验水准〉。H。:匚12=打(两总体方差相同)比:;「12=打(两总体方差不同)二-0.05(双侧检验)、计算检验统计量。2F=S|=Z689=1.80,1=9,2=9S242.72,1,2、查F界表,确定P值,下结论。查教材附表3方差起性检0.05/2,9,9-F0.05/2,9,9,P>0.05,按:=0.05水准,不拒绝H。,两组总体方差的差别无统计学意义,尚不能认为两组总体方差不等。可使用t检验对样本均数进行检验。样本均数的t检验:3验的F界值表,得F1、建立假设,确定检验水准a。H。J=0(左右手收缩压相同)Hi:「M0(左右手收缩压不相同)a=0.05.2、计算检验统计量。计算d值,见表1。恳二34.6/10=-3.46,2'di=-34.6,'di=215.76,带入公式送d2一近d)/nt=^=亠宀十1计算,有:sdSd/丿n下结论。查教材附表2,得,,p>0.05,按:.=0.05水准,接受Ho左右手测量值的差别没有统计学意义,可以认为男生左右手收缩压测量结果相同。表210位男生(惯用右手)在相同条件下左右手舒张压测量的结果编号左手舒张压平均(X?)右手舒张压平均(X2i)差=X2i-Xi):180717475.088848284.67-9.6793.5089273726971.367696466.674.6321.4369384737376.6770716769.37.3754.3169477767074.381847680.3-636568646465.372698071.3-636661605960.064696766.67-6.6744.4889764605961.064585358.32.77.29853777167.085817981.67-14.67215.2089983658176.381817980.33-4.0316.24091080798481.077777977.673.3311.0889合计707.87736.88-29.01535.5803一、从表2中可以看出,左手和右手的舒展压无明显的高低,呈现波动性,是否有差别需要进一步的检验。二、分析男生左右手舒张压是否有明显区别。解:Sd=”_[215.76-(-34.6)2/10Si一:10一1―346=1.12,9.80/、..103、查t界值表,确定P值,to.05/2,9=2.262,t0.05,按a=0.05水准,接受H0左右手测量值的差别没有统计学意义,可以认为男生左右手舒张压测量,右手的舒张压均数'2、建立假设,...