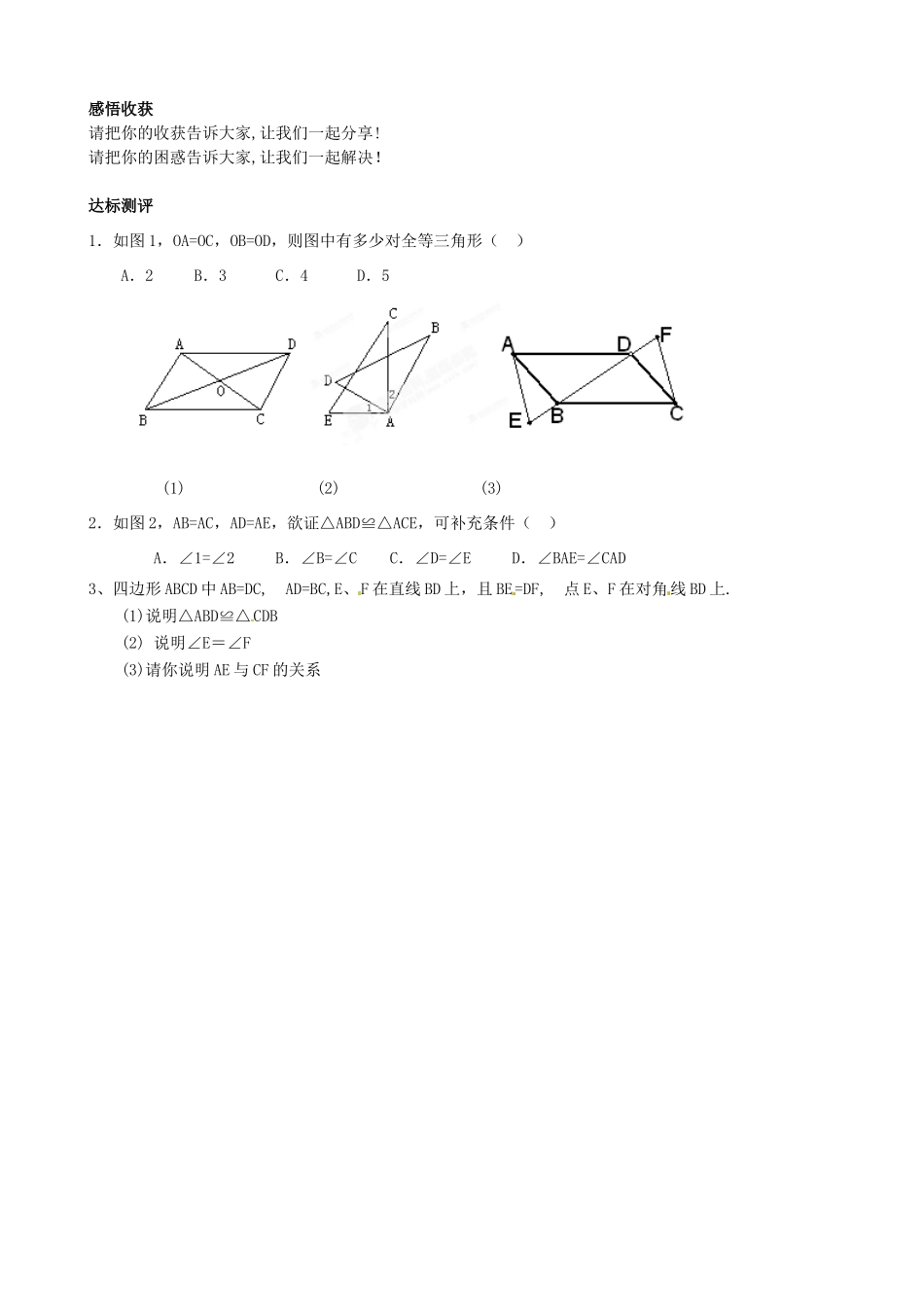
《全等三角形判定》教案学习目标:1、知识与技能目标:通过动手操作,合作交流、分析、归纳,让学生经历探索三角形全等的条件——“边角边”定理的过程,并掌握这种判定方法,并会用此定理进行简单的推理。2、过程与方法目标通过作图、交流和演示,使学生讨论探究出“边角边”定理,从而培养学生自主探究知识的意识以及团结协作解决问题的能力。3、情感态度与价值观目标:通过学生的动手实际操作、猜想和论证的过程,深化对知识的理解和方法的掌握,体验发现的快乐,体会成功探索的喜悦,激发学生学习数学的兴趣,培养学生热爱生活的思想感情,使学生从实际操作中获得数学知识,懂得数学知识来源于生活,又服务于生活的道理。学习重点:三角形全等的条件.学习难点:寻求三角形全等的条件.学习方法:启发诱导法知识链接:1、全等形:叫做全等形。2、全等三角形的性质:。学习过程:问题导学如图有一池塘。要测池塘两端A、B的距离,可无法直接达到,因此这两点的距离无法直接量出。你能想出办法来吗?探究活动一思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?已知△ABC,画一个△A′B′C′使AB=A′B′,AC=A′C′,∠A=∠A′。AAB思考:①△A′B′C′与△ABC全等吗?如何验正?请在小组内交流。展示归纳三角形全等的条件:和它们的对应相等的两个三角形全等,简写成“边角边”或“”数学符号语言:探究活动二两边及其中一边的对角对应相等的两个三角形全等吗?请在小组内交流。注:及其一边所对的相等,两个三角形不一定全等。初展身手1解决生活情景问题2.两车从南北方向的路段AB的A段出发,分别向东,向西行进相同的距离,到达C,D两地。此时C,D到B的距离相等吗?为什么?规律方法:。再露锋芒1.若AB=AC,则添加什么条件可得△ABD≌△ACD?2.如图:己知E、F都在直线AC上,AD∥BC,AF=CE,AD=BC,试说明DE=BF。AEBCFDBCABDC感悟收获请把你的收获告诉大家,让我们一起分享!请把你的困惑告诉大家,让我们一起解决!达标测评1.如图1,OA=OC,OB=OD,则图中有多少对全等三角形()A.2B.3C.4D.5(1)(2)(3)2.如图2,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件()A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD3、四边形ABCD中AB=DC,AD=BC,E、F在直线BD上,且BE=DF,点E、F在对角线BD上.(1)说明△ABD≌△CDB(2)说明∠E=∠F(3)请你说明AE与CF的关系