信号与系统期末试卷及答案VIP免费

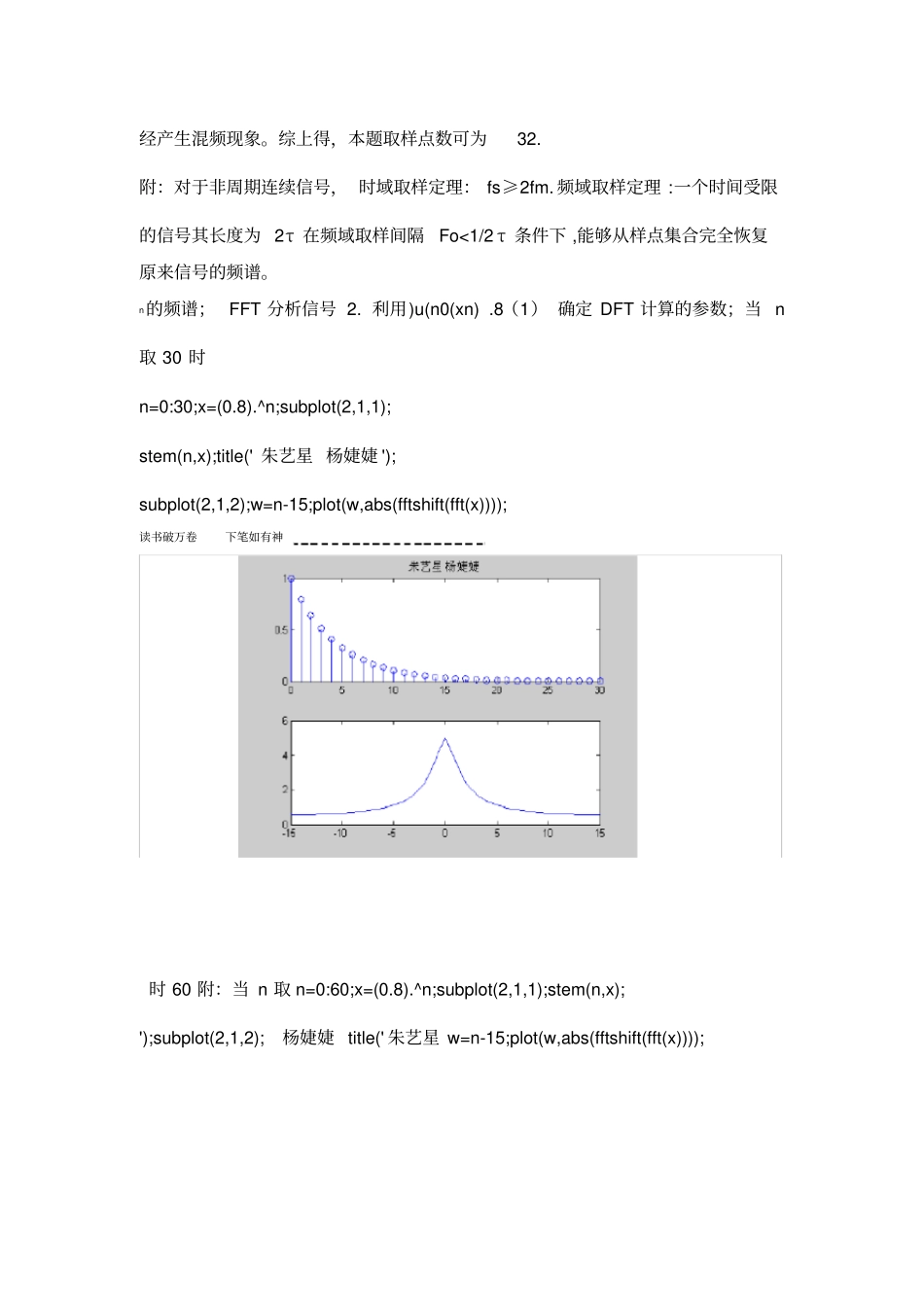
读书破万卷下笔如有神实验二利用DFT分析离散信号频谱一、实验目的应用离散傅里叶变换（DFT），分析离散信号的频谱。深刻理解DFT分析离散信号频谱的原理，掌握改善分析过程中产生的误差的方法。二、实验原理根据信号傅里叶变换建立的时域与频域之间的对应关系，可以得到有限长序列的离散傅里叶变换（DFT）与四种确定信号傅里叶变换之间的关系（见教材），实现由DFT分析其频谱。三、实验内容3的频谱；1.利用FFT分析信号x(310),nn,1,...,n)cos(8（1）、确定DFT计算的参数；N=32;n=0:N-1;x=cos(3*pi/8*n);X=fft(x,N);subplot(2,1,1);stem(n,abs(fftshift(X)));ylabel('Magnitude');xlabel('Frequency(rad)');title('朱艺星杨婕婕');subplot(2,1,2);stem(n,angle(fftshift(X)));ylabel('Phase');xlabel('Frequency(rad)');读书破万卷下笔如有神进行理论值与计算值比较，讨论信号频谱分析过程中误差原因及改善2）（方法。在频谱分析过程中由于取样频率过低或者由于信号的截取长度不当将会答：产生误差。可以适当提高取样率，增加样点数，可能会产生混频现象,取样频率过低,来减少混叠对频谱分析所造成的误差。对于连续周期信号，其时域取样必须kfo，即（其中K≥2*N+1N为最高谐波分量）其取样点数满足时域取样定理：2fm+fo。≥≥2Nfo+fo;fs截取信号长度不当，会产生功率泄露，对周期序列进行频谱分析时，为避免泄露应做到：截取的长度应取一个基本周期或基本周期的整数倍，若待分析的周期信号事先不知道其确切的周期，则可截取较长时间长度的样点进行分析，以减少功率泄露误差。当然，必须在取样频率满足取样定理的条件．读书破万卷下笔如有神下进行，否则混叠与泄露同时存在给频谱分析造成困难。3本题为周期信号，无直流分量，所以取样点数可为)ncos(n)x(82*N=32,但必须保证都是独立的样点。从取样点数N=32和N=16可以看出，取样点数的不同，会造成频率谱和相位谱的不同。当N=16时，n=3或-3时有幅度值，而在N=32时，n=-10和22时有幅度值，在N=64时，n=-20和44时有幅度值，得到在N=32时，其频谱已经和N=64时一致（刚好成2倍关系），且N=16时已经产生混频现象。综上得，本题取样点数可为32.附：对于非周期连续信号，时域取样定理：fs≥2fm.频域取样定理:一个时间受限的信号其长度为2τ在频域取样间隔Fo<1/2τ条件下,能够从样点集合完全恢复原来信号的频谱。n的频谱；FFT分析信号2.利用)u(n0(xn).8（1）确定DFT计算的参数；当n取30时n=0:30;x=(0.8).^n;subplot(2,1,1);stem(n,x);title('朱艺星杨婕婕');subplot(2,1,2);w=n-15;plot(w,abs(fftshift(fft(x))));读书破万卷下笔如有神时60附：当n取n=0:60;x=(0.8).^n;subplot(2,1,1);stem(n,x);');subplot(2,1,2);杨婕婕title('朱艺星w=n-15;plot(w,abs(fftshift(fft(x))));读书破万卷下笔如有神（2）进行理论值与计算值比较，讨论信号频谱分析过程中误差原因及改善方法。nx(n)0.8u(n)为离散非周期信号，且为无限长的信号。根据理答：信号论分析，一个时间有限的信号其频谱宽度为无限，一个时间无限的信号其频带宽度则为有限，因此，对一个时间有限的信号，应用DFT进行分析，频谱混叠难以避免。对一个时间无限的信号虽然频带有限，但在时间运算中，时间长度总是取有限值，所以频谱泄露难以避免。当原始信号事有限长，截取的长度等于原始信号的长度，则可以不考虑泄露的影响。当原始的非周期信号为无限长或比较长，而截取的长度有限或不等于原始信号的长度，则需考虑频谱泄露引起的不良影响。为了减少泄露的影响，一般可适当增加长度To，也可以通过试探法，先取长度N1（To=N1*T），然后取N2=2*N1,进行运算。若两者计算的结果很接近，则可取N1作为截取长度，否则继续去N3=2*N2,直至相邻两个长度的nx(n)0.8u(n)为计算结果相近，取长度较小的N为好。本题中，因为信号离散非周期信号，且为无限长的信号，用试探法：取n为30和60，进行比较，发现两者的频谱基本相似，所以取n为30较好。因为n取过大，fs提高，要求存贮单元增加，硬件速度提高，其结果势必在经济上和技术上带来新的问题。3.有限长脉冲序列，利用FFT分析其频谱。],50,1332nx()[,,,N=6;n=0:N-...