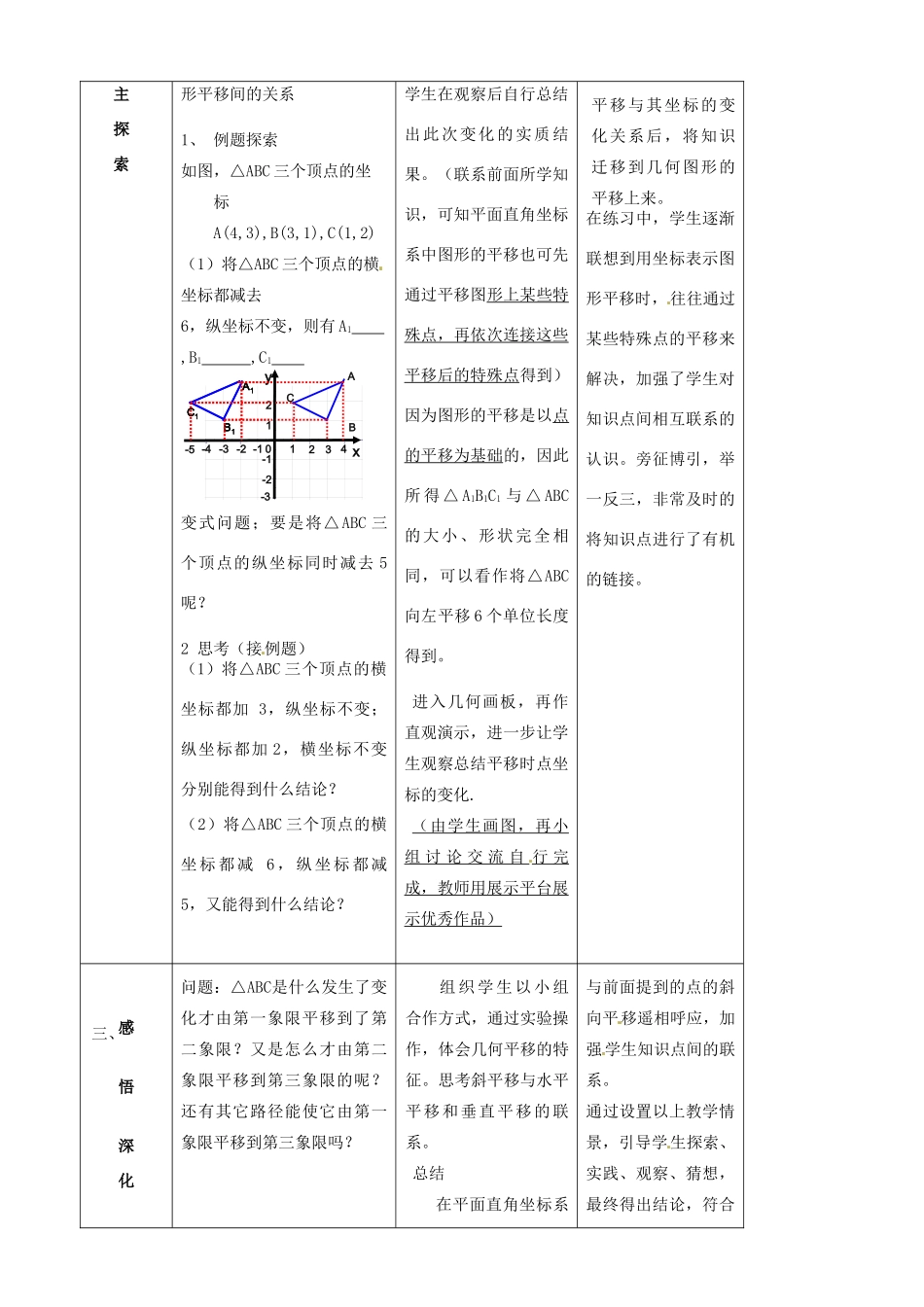
七年级数学下册第六章第6课时6.2.2用坐标表示平移(2)教案学校主备人时间设计理念探究线段的平移引起端点的坐标变化规律,初步具备数学创新的能力和动手操作、自主探索、合作交流的学习方式;明白研究对三角形、实物的平移引起对应点坐标变化规律可归结为研究图形顶点情况;将实际问题抽象成数学模型,用点的平移与坐标的变化规律解决简单实际问题,积累数学活动经验。教学目标知识与技能:掌握点的坐标变化与点的左右或上下平移间关系,掌握图形各个点的坐标变化与图形平移的关系并能够解决与平移相关的数学问题。过程与方法:经历探索点坐标变化与点平移的关系,图形各个点坐标变化与图形平移的关系过程,让学生学会独立自主地、有条理地思考、分析,解决、发展学生的形象思维能力和数形结合能力。情感态度与价值观:培养学生主动探索,敢于实践的合作创新精神,让学生学会主动寻求解决问题的途径,从成功中体会研究数学问题的成就感,从而增强学生学习数学的兴趣,树立学好数学的信心。在坐标系中,通过对点坐标的平移变化的探究,培养学生合作交流的意识和主动探索问题的精神.重点掌握坐标变化与图形平移的关系。难点利用坐标变化与图形平移的关系解决实际问题。方法实验、探究式教学法课型新授课教学过程教学环节教学内容师生活动设计意图复习回顾一、点的坐标变化与平移间的关系和规律?采用实验、观察、探索的学习方法,减少学生在学习过程中对教师的依赖,体现了“在参与中体验,在活动中发展”的全新理念。自探索图形点的坐标变化与图用幻灯片详细演示,让学生掌握点的主探索形平移间的关系1、例题探索如图,△ABC三个顶点的坐标A(4,3),B(3,1),C(1,2)(1)将△ABC三个顶点的横坐标都减去6,纵坐标不变,则有A1,B1,C121-1-2-3-4-2241234-1-2-3-412-1-2-3xyACB-5A1C1B1A1C1B10变式问题;要是将△ABC三个顶点的纵坐标同时减去5呢?2思考(接例题)(1)将△ABC三个顶点的横坐标都加3,纵坐标不变;纵坐标都加2,横坐标不变分别能得到什么结论?(2)将△ABC三个顶点的横坐标都减6,纵坐标都减5,又能得到什么结论?学生在观察后自行总结出此次变化的实质结果。(联系前面所学知识,可知平面直角坐标系中图形的平移也可先通过平移图形上某些特殊点,再依次连接这些平移后的特殊点得到)因为图形的平移是以点的平移为基础的,因此所得△A1B1C1与△ABC的大小、形状完全相同,可以看作将△ABC向左平移6个单位长度得到。进入几何画板,再作直观演示,进一步让学生观察总结平移时点坐标的变化.(由学生画图,再小组讨论交流自行完成,教师用展示平台展示优秀作品)平移与其坐标的变化关系后,将知识迁移到几何图形的平移上来。在练习中,学生逐渐联想到用坐标表示图形平移时,往往通过某些特殊点的平移来解决,加强了学生对知识点间相互联系的认识。旁征博引,举一反三,非常及时的将知识点进行了有机的链接。感悟深化问题:△ABC是什么发生了变化才由第一象限平移到了第二象限?又是怎么才由第二象限平移到第三象限的呢?还有其它路径能使它由第一象限平移到第三象限吗?组织学生以小组合作方式,通过实验操作,体会几何平移的特征。思考斜平移与水平平移和垂直平移的联系。总结在平面直角坐标系与前面提到的点的斜向平移遥相呼应,加强学生知识点间的联系。通过设置以上教学情景,引导学生探索、实践、观察、猜想,最终得出结论,符合三、内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数b,相应的新图形就是把原图形向上(或向下)平移b个单位长度。如果两者同时发生变化,那么图形就产生了水平与垂直的平移,即产生了斜平移。教育心理学指出的“感觉——知觉——记忆——思维——想象”的认知规律。四、巩固提高练习:.将长方形向左平移2个单位长度,再向上平移3个单位长度,画出平移后图形,指出顶点坐标学生以小组合作方式,通过实验操作,体会几何平移的特征。思考斜平移与水平平移和垂直平移的联系。与前面提到的点的斜向平移遥相呼应,加强学生知识点间的联系...